Chapter 7 - Coordinate Geometry, RD Sharma Solutions - (Part-8) | RD Sharma Solutions for Class 10 Mathematics PDF Download
Page No 6.30
Ques.45. Three vertices of a parallelogram are (a+b, a−b), (2a+b, 2a−b), (a−b, a+b). Find the fourth vertex.
Ans. Let ABCD be a parallelogram in which the co-ordinates of the vertices are;and. We have to find the co-ordinates of the forth vertex.
Let the forth vertex be D(x,y)
Since ABCD is a parallelogram, the diagonals bisect each other. Therefore the mid-point of the diagonals of the parallelogram will coincide. In general to find the mid-point P(x,y) of two points A(x1,y1) and B(x2,y2) we use section formula as,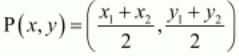
The mid-point of the diagonals of the parallelogram will coincide.
So,
Coordinate of mid-point of AC = Co-ordinate of mid-point of BD
Therefore,
Now equate the individual terms to get the unknown value. So,
x=-b
y=b
So the forth vertex is D(-b,b).
Page No 6.30
Ques.46. If two vertices of a parallelogram are (3, 2) (−1, 0) and the diagonals cut at (2, −5), find the other vertices of the parallelogram.
Ans. We have a parallelogram ABCD in which A (3, 2) and B (−1, 0) and the co-ordinate of the intersection of diagonals is M (2,−5).
We have to find the co-ordinates of vertices C and D.
So let the co-ordinates be C(x1,y1) and D(x2,y2)
In general to find the mid-point P(x,y) of two points A(x1,y1) and B(x2,y2) we use section formula as,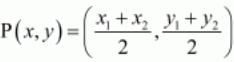
The mid-point of the diagonals of the parallelogram will coincide.
So,
Co-ordinate of mid-point of AC = Co-ordinate of M
Therefore,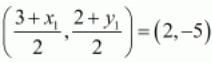
Now equate the individual terms to get the unknown value. So,
x = 1
y = -12
So the co-ordinate of vertex C is (1,−12)
Similarly,
Co-ordinate of mid-point of BD = Co-ordinate of M
Therefore,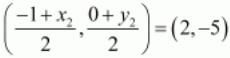
Now equate the individual terms to get the unknown value. So,
x= 5
y= -10
So the co-ordinate of vertex C is (5,−10)
Page No 6.30
Ques.47. If the coordinates of the mid-points of the sides of a triangle are (3, 4) (4, 6) and (5, 7), find its vertices.
Ans. The co-ordinates of the midpoint (xm,ym) between two points (x1,y1) and (x2,y2) is given by,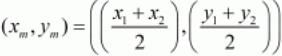
Let the three vertices of the triangle be A(xA, yA), B(xB,yB) and C(xC,yC).
The three midpoints are given. Let these points be MAB(3,4), MBC(4,6) and MCA(5,7).
Let us now equate these points using the earlier mentioned formula,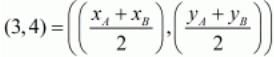
Equating the individual components we get,
xA + xB = 6
yA + yB = 8
Using the midpoint of another side we have,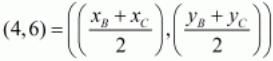
Equating the individual components we get,
xB + xC = 8
yB + yC = 12
Using the midpoint of the last side we have,
Equating the individual components we get,
xA + xC = 10
yA + yC = 14
Adding up all the three equations which have variable ‘x’ alone we have,
xA + xB + xB + xC + xA + xC = 6 + 8 + 10
2(xA + xB + xC) = 24
xA + xB + xC = 12
Substituting xB + xC = 4 in the above equation we have,
xA + xB + xC = 12
xA + 8 = 12
xA = 4
Therefore,
xA + xC = 10
xC = 10 - 4
xC = 6
And
xA + xB = 6
xB = 6 - 4
xB = 2
Adding up all the three equations which have variable ‘y’ alone we have,
yA + yB + yB + yC + yA + yC = 8 + 12 + 14
2(yA + yB + yC) = 34
yA + yB + yC = 17
Substituting yB + yC = 12 in the above equation we have,
yA + yB + yC = 17
yA + 12 = 17
yA = 5
Therefore,
yA + yC = 14
yC = 14-5
yC = 9
And
yA + yB = 8
yB = 8-5
yB = 3
Therefore the co-ordinates of the three vertices of the triangle are  .
.
Page No 6.30
Ques.48. The line segment joining the points P(3, 3) and Q(6, −6) is trisected at the points A and B such that A is nearer to P. If A also lies on the line given by 2x + y + k = 0, find the value of k.
Ans. We have two points P (3, 3) and Q (6,−6). There are two points A and B which trisect the line segment joining P and Q.
Let the co-ordinate of A be A(x1,y1)
Now according to the section formula if any point P divides a line segment joining A(x1,y1) and B(x2,y2) in the ratio m: n internally than,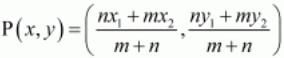
The point A is the point of trisection of the line segment PQ. So, A divides PQ in the ratio 1: 2
Now we will use section formula to find the co-ordinates of unknown point A as,
Therefore, co-ordinates of point A is(4, 0)
It is given that point A lies on the line whose equation is
2x+y+k=0
So point A will satisfy this equation.
2(4)+0+k=0
So,
k=-8
Page No 6.30
Ques.49. If three consecutive vertices of a parallelogram are (1, −2), (3, 6) and (5, 10), find its fourth vertex.
Ans.
Let ABCD be a parallelogram in which the co-ordinates of the vertices are A (1,−2);
B (3, 6) and C(5, 10). We have to find the co-ordinates of the forth vertex.
Let the forth vertex be D(x,y)
Since ABCD is a parallelogram, the diagonals bisect each other. Therefore the mid-point of the diagonals of the parallelogram will coincide.
Now to find the mid-point P(x,y) of two points A(x1,y1) and B(x2,y2) we use section formula as,
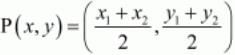
The mid-point of the diagonals of the parallelogram will coincide.
So,
Co-ordinate of mid-point of AC = Co-ordinate of mid-point of BD
Therefore,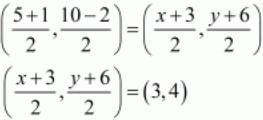
Now equate the individual terms to get the unknown value. So,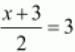
x=3
Similarly,
y=2
So the forth vertex is D(3,2)
Page No 6.30
Ques.50.
(i) If the points A (a, −11), B (5, b), C(2, 15) and D (1, 1) are the vertices of a parallelogram ABCD, find the values of a and b.
(ii) Point A(3, 1), B(5, 1), C(a, b) and D(4, 3) are vertices of a parallelogram ABCD. Find the values of a and b.
Ans. (i) Let ABCD be a parallelogram in which the co-ordinates of the vertices are A (a,−11); B (5, b); C (2, 15) and D (1, 1).
Since ABCD is a parallelogram, the diagonals bisect each other. Therefore the mid-point of the diagonals of the parallelogram will coincide.
In general to find the mid-point P(x,y) of two points A(x1,y1) and B(x2,y2) we use section formula as,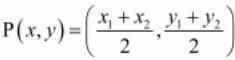
The mid-point of the diagonals of the parallelogram will coincide.
So,
Co-ordinate of mid-point of AC = Co-ordinate of mid-point of BD
Therefore,
Now equate the individual terms to get the unknown value. So,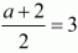
Similarly,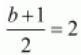
b=3
Therefore,
a=4, b=3
(ii) Given: Point A(3, 1), B(5, 1), C(a, b) and D(4, 3) are vertices of a parallelogram ABCD.
Diagonals of a parallelogram bisect each other.
∴ Mid point of AC = Mid point of BD
Mid point of (x1, y1) and (x2, y2) is 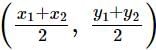 .
.
Mid point of AC=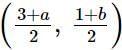
Mid point of BD=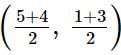
=(9/2, 4/2)=(9/2, 2)
∴
⇒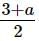 = 9/2 and
= 9/2 and 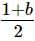 =2
=2
⇒3+a=9 and 1+b=4
⇒a=6 and b=3
Hence, the values of a and b is 6 and 3, respectively.
Page No 6.31
Ques.51. If the coordinates of the mid-points of the sides of a triangle be (3, −2), (−3, 1) and (4, −3), then find the coordinates of its vertices.
Ans. The co-ordinates of the midpoint (xm,xn) between two points (x1,y1) and (x2,y2) is given by,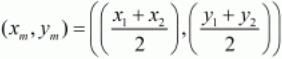
Let the three vertices of the triangle be A(xA,yA), B(xB,yB) and C(xC,yC).
The three midpoints are given. Let these points be MAB(3,-2), MBC(-3,1) and MCA(4,-3).
Let us now equate these points using the earlier mentioned formula,
Equating the individual components we get,
xA + xB = 6
yA + yB = -4
Using the midpoint of another side we have,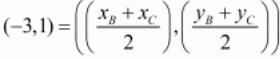
Equating the individual components we get,
xB + xC = -6
yB + yC = 2
Using the midpoint of the last side we have,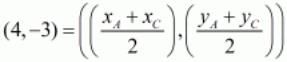
Equating the individual components we get,
xA + xC = 8
yA + yC = -6
Adding up all the three equations which have variable ‘x’ alone we have,
xA + xB + xB + xC + xA + xC = 6-6+8
2(xA + xB + xC) = 8
xA + xB + xC = 4
Substituting xB + xC = -6 in the above equation we have,
xA + xB + xC = 4
xA - 6 = 4
xA = 10
Therefore,
xA + xC = 8
xC = 8 - 10
xC = -2
And
xA + xB = 6
xB = 6 - 10
xB = -4
Adding up all the three equations which have variable ‘y’ alone we have,
yA + yB + yB + yC + yA + yC = -4+2-6
2(yA + yB + yC) = -8
yA + yB + yC = -4
Substituting yB + yC = 2 in the above equation we have,
yA + yB + yC = -4
yA + 2 = -4
yA = -6
Therefore,
yA + yC = -6
yC = -6 + 6
yC = 0
And
yA + yB = -4
yB = -4 + 6
yB = 2
Therefore the co-ordinates of the three vertices of the triangle are .
.
Page No 6.31
Ques.52.
(i) Points P and Q trisect the line segment joining the points A(–2, 0) and B(0, 8) such that P is near to A. Find the coordinates of P and Q.
(ii) The line segment joining the points (3, −4) and (1, 2) is trisected at the points P and Q. If the coordinates of P and Q are (p, −2) and (5/3, q) respectively. Find the values of p and q.
Ans. (ii) Let the points A(3, −4) and B(1, 2) is trisected at the points P(p, −2) and Q(5/3, q).
Thus, AP = PQ = QB
Therefore, P divides AB internally in the ratio 1 : 2.
Section formula: if the point (x, y) divides the line segment joining the points (x1, y1) and (x2, y2) internally in the ratio m : n, then the coordinates (x, y) = (mx2+nx1m+n, my2+ny1m+n)mx2+nx1m+n, my2+ny1m+n
Therefore, using section formula, the coordinates of P are:
(p, −2)=(1(1)+2(3)1+2,1(2)+2(−4)1+2)⇒(p, −2)=(1+63,2−83)⇒(p, −2)=(73,−63)⇒(p, −2)=(73,−2)⇒p=73p, -2=11+231+2,12+2-41+2⇒p, -2=1+63,2-83⇒p, -2=73,-63⇒p, -2=73,-2⇒p=73
Also, Q divides AB internally in the ratio 2 : 1.
Therefore, using section formula, the coordinates of Q are:
(53, q)=(2(1)+1(3)2+1,2(2)+1(−4)2+1)⇒(53, q)=(2+33,4−43)⇒(53, q)=(53,03)⇒(53, q)=(53,0)⇒q=053, q=21+132+1,22+1-42+1⇒53, q=2+33,4-43⇒53, q=53,03⇒53, q=53,0⇒q=0
Hence, the values of p and q is 7373 and 0, respectively.
Page No 6.31:
Question 53:
The line joining the points (2, 1) and (5, −8) is trisected at the points P and Q. If point P lies on the line 2x − y + k = 0. Find the value of k.
ANSWER:
We have two points A (2, 1) and B (5,−8). There are two points P and Q which trisect the line segment joining A and B.
Now according to the section formula if any point P divides a line segment joining andin the ratio m: n internally than,
The point P is the point of trisection of the line segment AB. So, P divides AB in the ratio 1: 2
Now we will use section formula to find the co-ordinates of unknown point A as,
Therefore, co-ordinates of point P is(3,−2)
It is given that point P lies on the line whose equation is
So point A will satisfy this equation.
So,
Page No 6.31:
Question 54:
A (4, 2), B(6, 5) and C (1, 4) are the vertices of ΔABC.
(i) The median from A meets BC in D. Find the coordinates of the point D.
(ii) Find the coordinates of point P and AD such that AP : PD = 2 : 1.
(iii) Find the coordinates of the points Q and R on medians BE and CF respectively such that BQ : QE = 2 : 1 and CR : RF = 2 : 1
(iv) What do you observe?
ANSWER:
We have triangle in which the co-ordinates of the vertices are A (4, 2); B (6, 5) and C (1, 4)
(i)It is given that median from vertex A meets BC at D. So, D is the mid-point of side BC.
In general to find the mid-point of two pointsand we use section formula as,
Therefore mid-point D of side BC can be written as,
Now equate the individual terms to get,
So co-ordinates of D is
(ii)We have to find the co-ordinates of a point P which divides AD in the ratio 2: 1 internally.
Now according to the section formula if any point P divides a line segment joining andin the ratio m: n internally than,
P divides AD in the ratio 2: 1. So,
(iii)We need to find the mid-point of sides AB and AC. Let the mid-points be F and E for the sides AB and AC respectively.
Therefore mid-point F of side AB can be written as,
So co-ordinates of F is
Similarly mid-point E of side AC can be written as,
So co-ordinates of E is
Q divides BE in the ratio 2: 1. So,
Similarly, R divides CF in the ratio 2: 1. So,
(iv)We observe that that the point P, Q and R coincides with the centroid. This also shows that centroid divides the median in the ratio 2: 1.
Page No 6.31:
Question 55:
If the points A (6, 1), B (8, 2), C (9, 4) and D (k, p) are the vertices of a parallelogram taken in order, then find the values of k and p.
ANSWER:
Let ABCD be a parallelogram in which the co-ordinates of the vertices are A (6, 1); B (8, 2); C (9, 4) and D (k, p).
Since ABCD is a parallelogram, the diagonals bisect each other. Therefore the mid-point of the diagonals of the parallelogram will coincide.
In general to find the mid-point of two pointsand we use section formula as,
The mid-point of the diagonals of the parallelogram will coincide.
So,
Therefore,
Now equate the individual terms to get the unknown value. So,
Similarly,
Therefore,
FAQs on Chapter 7 - Coordinate Geometry, RD Sharma Solutions - (Part-8) - RD Sharma Solutions for Class 10 Mathematics
| 1. What are the basic concepts of coordinate geometry? |  |
| 2. How is the distance between two points calculated in coordinate geometry? |  |
| 3. What is the slope of a line in coordinate geometry? |  |
| 4. How is the midpoint of a line segment calculated in coordinate geometry? |  |
| 5. What are the different forms of equations of a line in coordinate geometry? |  |

|
Explore Courses for Class 10 exam
|

|
















