Polynomials (Exercise 2.2 & 2.3) RD Sharma Solutions | Advance Learner Course: Mathematics (Maths) Class 9 PDF Download
Exercise 2.2
Question: 1
Verify that the numbers given alongside the cubic polynomials below are their zeroes. Also, verify the relationship between the zeroes and coefficients in each of the following cases:
(i) f(x) = 2x3+ x2– 5x + 2; 1/2, 1, – 2
(ii) g(x) = x3– 4x2 + 5x – 2; 2, 1, 1
Solution:
(i) f(x) = 2x3 + x2 – 5x + 2; 1/2, 1, – 2
(a) By putting x = 1/2 in the above equation, we will get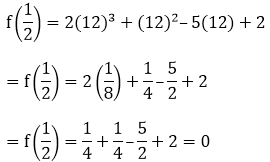
(b) By putting x = 1 in the above equation, we will get
f(1) = 2(1)3 + (1)2 – 5(1) + 2
= 2 + 1 – 5 + 2 = 0
(c) By putting x = -2 in the above equation, we will get
f(−2) = 2(−2)3 + (−2)2 – 5(−2) + 2
= -16 + 4 + 10 + 2 = – 16 + 16 = 0
Now,
Sum of zeroes = α + β + γ = - b/a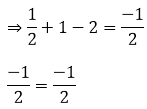
Product of the zeroes = αβ + βγ + αγ = c/a
Hence, verified.
(ii) g(x) = x3 – 4x2 + 5x – 2; 2, 1, 1
(a) By putting x = 2 in the given equation, we will get
g(2) = (2)3 – 4(2)2 + 5(2) – 2
= 8 – 16 + 10 – 2 = 18 – 18 = 0
(b) By putting x = 1 in the given equation, we will get
g(1) = (1)3 – 4(1)2 + 5(1) – 2
= 1 – 4 + 5 – 2
= 0
Now,
Sum of zeroes= α + β + γ =-b/a
⇒ 2 + 1 + 1 = −(−4)
4 = 4
Product of the zeroes = αβ + βγ + αγ = c/a
2 × 1 + 1 × 1 + 1 × 2 = 5
2 + 1 + 2 = 5
5 = 5
αβγ = –(−2)
2 × 1 × 1 = 2
2 = 2
Hence, verified.
Question: 2
Find a cubic polynomial with the sum, sum of the product of its zeroes is taken two at a time, and product of its zeroes as 3, – 1 and – 3 respectively.
Solution:
Any cubic polynomial is of the form ax3 + bx2 + cx + d:
= x3 – (sum of the zeroes) x2 + (sum of the products of its zeroes) x – (product of the zeroes)
= x3 – 3x2 + (−1)x + (−3)
= k[x3 – 3x2 – x – 3]
k is any non-zero real numbers.
Question: 3
If the zeroes of the polynomial f(x) = 2x3 – 15x2 + 37x – 30, find them.
Solution:
Let, α = a – d, β = a and γ = a + d be the zeroes of the polynomial.
f(x) = 2x3 – 15x2 + 37x – 30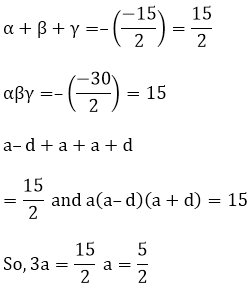
And, a (a2 + d2) = 15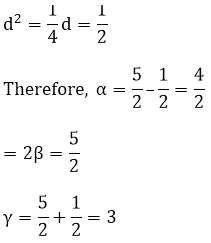
Question: 4
Find the condition that the zeroes of the polynomial f(x) = x3 + 3px2 + 3qx + r may be in A.P.
Solution:
f(x) = x3 + 3px2 + 3qx + r
Let, a – d, a, a + d be the zeroes of the polynomial.
Then,
The sum of zeroes = – b/a
a + a – d + a + d = -3p 3a = -3p a = -p Since, a is the zero of the polynomial f(x),
Therefore, f(a) = 0
f(a) = a3 + 3pa2 + 3qa + r = 0
Therefore, f(a) = 0f(a) = 0
⇒ a3 + 3pa2 + 3qa + r = 0
= ⇒ (−p)3 + 3p(−p)2 + 3q(−p) + r = 0
= − p3 + 3p3 – pq + r = 0
= 2p3 – pq + r = 0
Question: 5
If zeroes of the polynomial f(x) = ax3 + 3bx2 + 3cx + d are tin A.P., prove that 2b3 – 3abc + a2d = 0.
Solution:
f(x) = x3 + 3px2 + 3qx + r
Let, a – d, a, a + d be the zeroes of the polynomial.
Then,
The sum of zeroes = - b/a
a + a – d + a + d = – 3b/a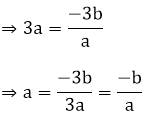
Since, f(a) = 0
⇒ a(a2) + 3b(a)2 + 3c(a) + d = 0
⇒ a(a2) + 3b(a)2 + 3c(a) + d = 0 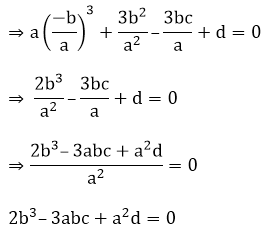
Question: 6
If the zeroes of the polynomial f(x) = x3 – 12x2 + 39x + k are in A.P., find the value of k.
Solution:
f(x) = x3 – 12x2 + 39x + k
Let, a-d, a, a + d be the zeroes of the polynomial f(x).
The sum of the zeroes = 12
3a = 12
a = 4
Now,
f(a) = 0
f(a) = a3 – 12a2 + 39a + k f(4) = 43 – 12(4)2 + 39(4) + k = 0
f(4) = 43 –12(4)2 + 39(4) + k = 0
64 – 192 + 156 + k = 0
k = – 28
Exercise 2.3
Question: 1
Apply division algorithm to find the quotient q(x) and remainder r(x) on dividing f(x) by g(x) in each of the following:
(i) f(x) = x3 – 6x2 + 11x – 6, g(x) = x2 + x + 1
(ii) f(x) = 10x4 + 17x3 – 62x2 + 30x – 105, g(x) = 2x2 + 7x + 1
(iii) f(x) = 4x3 + 8x2 + 8x + 7, g(x) = 2x2 – x + 1
(iv) f(x) = 15x3 – 20x2 + 13x – 12, g(x) = x2 – 2x + 2
Solution:
(i) f(x) = x3 – 6x2 + 11x – 6 and g(x) = x2 + x + 1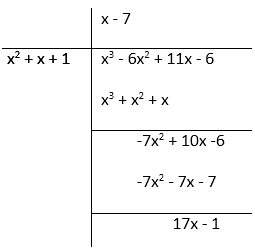
(ii) f(x) = 10x4 + 17x3 – 62x2 + 30x – 105, g(x) = 2x2 + 7x + 1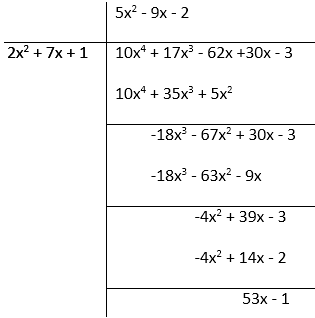
(iii) f(x) = 4x3 + 8x2 + 8x + 7, g(x) = 2x2 – x + 1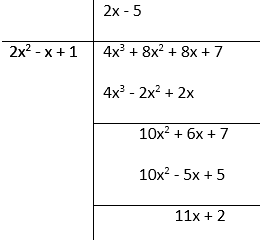
(iv) f(x) = 15x3 – 20x2 + 13x – 12, g(x) = x2 – 2x + 2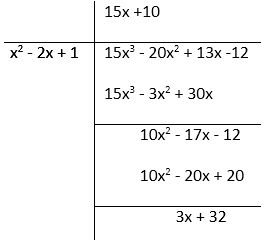
Question: 2
Check whether the first polynomial is a factor of the second polynomial by applying the division algorithm:
(i) g(t) = t2 – 3; f(t) = 2t4 + 3t3 – 2t2 – 9t – 12
(ii) g(x) = x2 – 3x + 1; f(x) = x5 – 4x3 + x2 + 3x + 1
(iii) g(x) = 2x2 – x + 3; f(x) = 6x5 − x4 + 4x3 – 5x2 – x – 15
Solution:
(i) g(t) = t2 – 3; f(t) = 2t4 + 3t3 – 2t2 – 9t – 12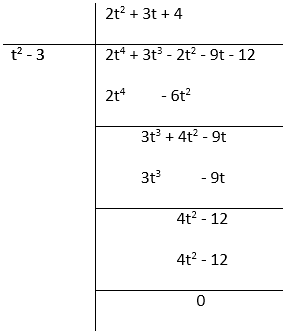
g(t) = t2 – 3g(t) = t2 – 3 f(t) = 2t4 + 3t3 – 2t2 – 9t Therefore, g(t) is the factor of f(t).
(ii) g(x) = x2 – 3x + 1; f(x) = x5 – 4x3 + x2 + 3x + 1

g(x) = x2 – 3x + 1 g(x) = x2 – 3x + 1 f(x) = x5 – 4x3 + x2 + 3x + 1.Therefore, g(x) is not the factor of f(x).
(iii) g(x) = 2x2 – x + 3; f(x) = 6x5 − x4 + 4x3 – 5x2 – x – 15
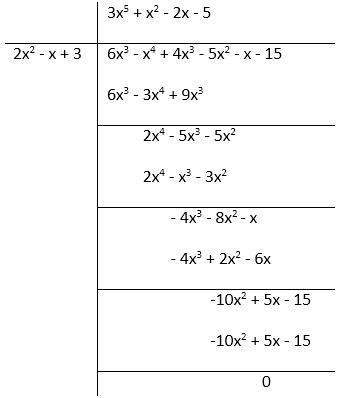
g(x) = 2x2 – x + 3 g(x) = 2x2 – x + 3 f(x) = 6x5 − x4 + 4x3 – 5x2 – x – 15
Question: 3
Obtain all zeroes of the polynomial f(x) = f(x) = 2x4 + x3 – 14x2 – 19x – 6, if two of its zeroes are -2 and -1.
Solution:
f(x) = 2x4 + x3 – 14x2 – 19x – 6
If the two zeroes of the polynomial are -2 and -1, then its factors are (x + 2) and (x + 1)
(x + 2)(x + 1) = x2 + x + 2x + 2 = x2 + 3x + 2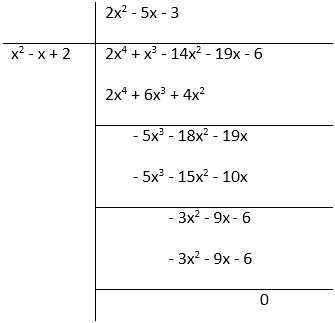
f(x) = 2x4 + x3 – 14x2 – 19x – 6 = (2x2 – 5x – 3)(x2 + 3x + 2)
= (2x + 1)(x – 3)(x + 2)(x + 1)
Therefore, zeroes of the polynomial = - 1/2, 3, -2 , -1
Question: 4
Obtain all zeroes of f(x) = x3 + 13x2 + 32x + 20, if one of its zeroes is -2.
Solution:
f(x) = x3 + 13x2 + 32x + 20
Since, the zero of the polynomial is -2 so, it means its factor is (x + 2).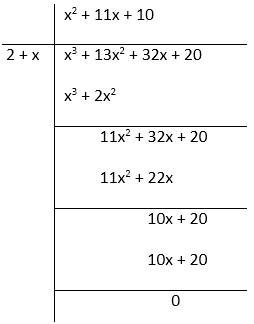
So, f(x) = x3 + 13x2 + 32x + 20 = (x2 + 11x + 10)(x + 2)
= (x2 + 10x + x + 10)(x + 2)
= (x + 10)(x + 1)(x + 2)
Therefore, the zeroes of the polynomial are – 1, – 10, – 2.
Question: 5
Obtain all zeroes of the polynomial f(x) = x4 – 3x3 – x2 + 9x – 6, if the two of its zeroes are – √3 and √3.
Solution:
f(x) = x4 – 3x3 – x2 + 9x – 6 Since, two of the zeroes of polynomial are -√3 and √3 so,(x + √3)(x – √3) = x2– 3x2 – 3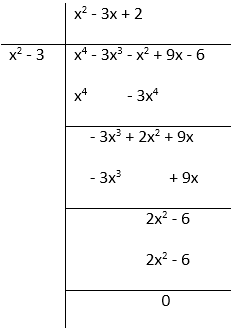
So, f(x) = x4 – 3x2 – x2 + 9x – 6 = (x2 – 3)(x2 – 3x + 2)
= (x + √3)(x – √3)x2– 2x – 2 + 2)
= (x + √3)(x – √3)(x – 1)(x – 2)
Therefore, the zeroes of the polynomial are - √3, √3, 1, 2.
Question: 6
Obtain all zeroes of the polynomial f(x) = 2x4 – 2x3 – 7x2 + x – 1, if the two of its zeroes are – √(3/2) and √(3/2).
Solution:
f(x) = 2x4 – 2x3 – 7x2 + x – 1 Since, - √(3/2) and √(3/2) are the zeroes of the polynomial, so the factors are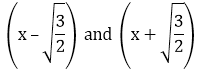
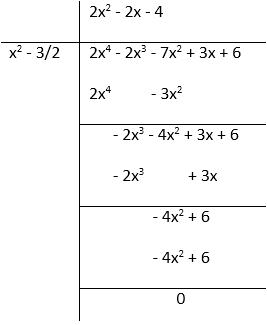
So, f(x) = 2x4– 2x3–7x2+ x – 1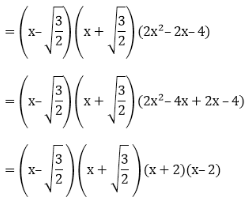
Therefore, the zeroes of the polynomial = x = -1, 2, -√(3/2) and √(3/2).
Question: 7
Find all the zeroes of the polynomial x4 + x3 – 34x2 – 4x + 120, if the two of its zeroes are 2 and – 2.
Solution:
x4 + x3 – 34x2 – 4x + 120 Since, the two zeroes of the polynomial given is 2 and – 2 So, factors are (x + 2)(x – 2) = x2 + 2x – 2x – 4 = x2 – 4x2 – 4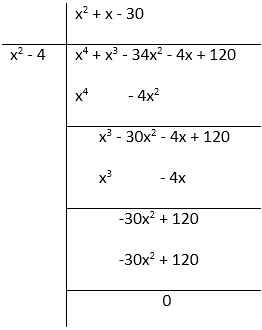
So, x4 + x3 – 34x2 – 4x + 120 = (x2 – 4)(x2 + x – 30)
= (x – 2)(x + 2)(x2 + 6x – 5x – 30)
= (x – 2)(x + 2)(x + 6)(x – 5)
Therefore, the zeroes of the polynomial = x = 2, – 2, – 6, 5
Question: 8
Find all the zeroes of the polynomial 2x4 + 7x3 – 19x2 – 14x + 30, if the two of its zeroes are √2 and - √2.
Solution:
2x4 + 7x3 – 19x2 – 14x + 302 Since, √2 and-√2 are the zeroes of the polynomial given. So, factors are (x + √2) and (x - √2)
= x2+√2x – √2x – 2 = x2 – 2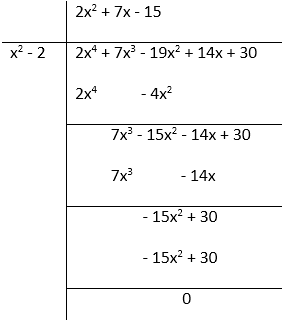
So, 2x4 + 7x3 – 19x2 – 14x + 30 = (x2 – 2)(2x2 + 7x – 15)
= (2x2+ 10x – 3x – 15)(x + √2)(x – √2)
= (2x – 3)(x + 5)(x + √2)(x – √2)
Therefore, the zeroes of the polynomial is √2,- √2,-5, 3/2.
Question: 9
Find all the zeroes of the polynomial f(x) = 2x3 + x2 – 6x – 3, if two of its zeroes are – √3 and √3.
Solution:
f(x) = 2x3 + x2 – 6x – 3 Since, -√3 and √3 are the zeroes of the given polynomial So, factors are (x - √3) and (x + √3)
= (x2– √3x + √3x – 3) = (x2 – 3)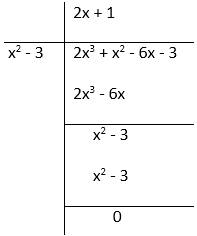
So, f(x) = 2x3 + x2 – 6x – 3 = (x2 – 3)(2x + 1)
= (x – √3)(x + √3)(2x + 1)
Therefore, set of zeroes for the given polynomial = √3,– √3, –1/2
Question: 10
Find all the zeroes of the polynomial f(x) = x3 + 3x2 – 2x – 6, if the two of its zeroes are √2 and - √2.
Solution:
f(x) = x3 + 3x2 – 2x – 6 Since, √2 and -√2 are the two zeroes of the given polynomial. So, factors are (x + √2) and (x - √2)
= x2+ √2x – √2x – 2 = x2 – 2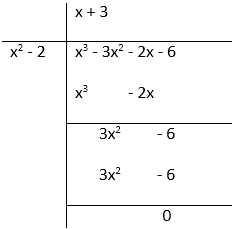
By division algorithm, we have:
f(x) = x3 + 3x2 – 2x – 6 = (x2 – 2)(x + 3)
= (x – √2)(x + √2)(x + 3)
Therefore, the zeroes of the given polynomial is - √2, √2 and – 3.
Question: 11
What must be added to the polynomial f(x) = x4 + 2x3 – 2x2 + x − 1 so that the resulting polynomial is exactly divisible by g(x) = x2 + 2x − 3.
Solution:
f(x) = x4 + 2x3 – 2x2 + x − 1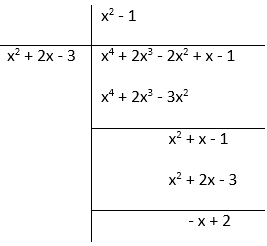
We must add (x – 2) in order to get the resulting polynomial exactly divisible by g(x) = x2 + 2x − 3.
Question: 12
What must be subtracted from the polynomial f(x) = x4 + 2x3 – 13x2 –12x + 21 so that the resulting polynomial is exactly divisible by g(x) = x2 – 4x + 3.
Solution:
f(x) = x4 + 2x3 – 13x2 – 12x + 21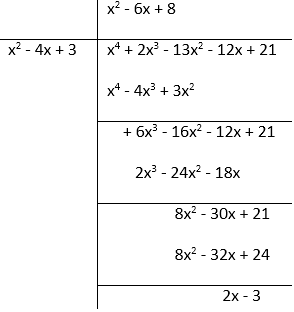
We must subtract (2x – 3) in order to get the resulting polynomial exactly divisible by g(x) = x2 – 4x + 3.
Question: 13
Given that √2 is a zero of the cubic polynomial f(x) = 6x3+ √2x2– 10x – 4√2, find its other two zeroes.
Solution:
f(x) = 6x3+√2x2 – 10x – 4√2 Since, √2 is a zero of the cubic polynomial So, factor is (x–√2)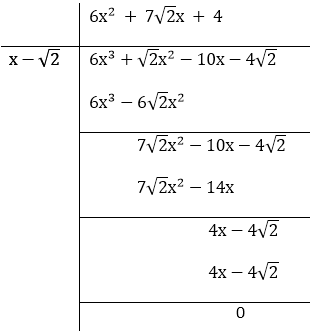
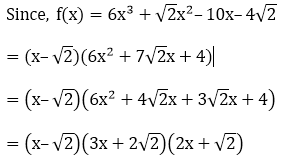

Question: 14
Given that x – √5 is a factor of the cubic polynomial 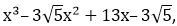 find all the zeroes of the polynomial.
find all the zeroes of the polynomial.
Solution:
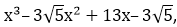
In the question, it’s given that x – √5 is a factor of the cubic polynomial.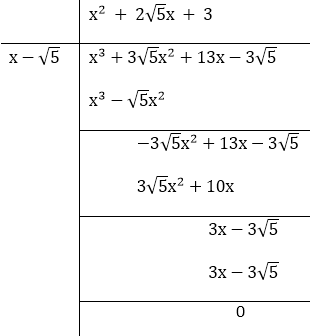
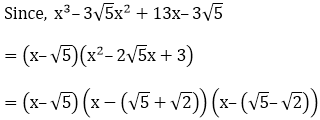
So, the zeroes of the polynomial 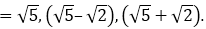
|
13 videos|79 docs|29 tests
|
FAQs on Polynomials (Exercise 2.2 & 2.3) RD Sharma Solutions - Advance Learner Course: Mathematics (Maths) Class 9
| 1. What are polynomials and how are they defined? |  |
| 2. How can we classify polynomials based on their degrees? |  |
| 3. Can a polynomial have more than one variable? |  |
| 4. How can we perform operations like addition, subtraction, and multiplication on polynomials? |  |
| 5. What are the zeros of a polynomial and how can we find them? |  |
















