Important Permutations & Combinations Formulas for JEE and NEET
DEFINITIONS :
1. PERMUTATION : Each of the arrangements in a definite order which can be made by taking some or all of a number of things is called a PERMUTATION.
2.COMBINATION : Each of the groups or selections which can be made by taking some or all of a number of things without reference to the order of the things in each group is called a COMBINATION.
FUNDAMENTAL PRINCIPLE OF COUNTING :
If an event can occur in ‘m’ different ways, following which another event can occur in ‘n’ different ways, then the total number of different ways of simultaneous occurrence of both events in a definite order is m × n. This can be extended to any number of events.
RESULTS : (i) A Useful Notation : n! = n (n − 1) (n − 2)......... 3. 2. 1 ; n ! = n. (n − 1) !0! = 1! = 1 ; (2n)! = 2n. n ! [1. 3. 5. 7...(2n − 1)] Note that factorials of negative integers are not defined.
(ii) If nPr denotes the number of permutations of n different things, taking r at a time, then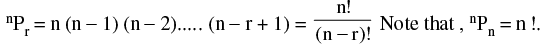
(iii) If nCr denotes the number of combinations of n different things taken r at a time, then 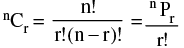 where r ≤ n ; n ∈ N and r ∈ W.
where r ≤ n ; n ∈ N and r ∈ W.
(iv) The number of ways in which (m + n) different things can be divided into two groups containing m & n things respectively is : 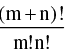 If m = n, the groups are equal & in this case the number of subdivision is
If m = n, the groups are equal & in this case the number of subdivision is 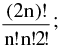 for in any one way it is possible to interchange the two groups without obtaining a new distribution. However, if 2n things are to be divided equally between two persons then the number of ways =
for in any one way it is possible to interchange the two groups without obtaining a new distribution. However, if 2n things are to be divided equally between two persons then the number of ways = 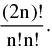
(v) Number of ways in which (m + n + p) different things can be divided into three groups containing m , n & p things respectively is 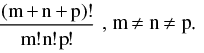
If m = n = p then the number of groups =  However, if 3n things are to be divided equally among three people then the number of ways
However, if 3n things are to be divided equally among three people then the number of ways 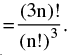
(vi)The number of permutations of n things taken all at a time when p of them are similar & of one type, q of them are similar & of another type, r of them are similar & of a third type & the remaining n – (p + q + r) are all different is : 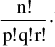
(vii) The number of circular permutations of n different things taken all at a time is ; (n − 1)!. If clockwise & anti−clockwise circular permutations are considered to be same, then it is 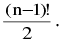
Note : Number of circular permutations of n things when p alike and the rest different taken all at a time distinguishing clockwise and anticlockwise arrangement is 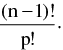
(viii) Given n different objects, the number of ways of selecting at least one of them is, nC1 + nC2 + nC3 +.....+ nCn = 2n − 1. This can also be stated as the total number of combinations of n distinct things.
(ix) Total number of ways in which it is possible to make a selection by taking some or all out of p + q + r +...... things , where p are alike of one kind, q alike of a second kind , r alike of third kind & so on is given by : (p + 1) (q + 1) (r + 1)........ –1.
(x) Number of ways in which it is possible to make a selection of m + n + p = N things , where p are alike of one kind , m alike of second kind & n alike of third kind taken r at a time is given by coefficient of xr in the expansion of (1 + x + x2 +...... + xp) (1 + x + x2 +...... + xm) (1 + x + x2 +...... + xn).
Note : Remember that coefficient of xr in (1 − x)−n = n+r−1Cr (n ∈ N). For example the number of ways in which a selection of four letters can be made from the letters of the word PROPORTION is given by coefficient of x4 in (1 + x + x2 + x3) (1 + x + x2) (1 + x + x2) (1 + x) (1 + x) (1 + x).
(xi) Number of ways in which n distinct things can be distributed to p persons if there is no restriction to the number of things received by men = pn.
(xii) Number of ways in which n identical things may be distributed among p persons if each person may receive none , one or more things is ; n+p−1Cn.
a. nCr = nCn−r ; nC0 = nCn = 1;
b. nCx = nCy ⇒ x = y or x + y = n
c. nCr + nCr−1 = n+1Cr
(xiv) nCr is maximum if :
(a) r = n/2 if n is even.
(b) r = 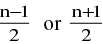 if n is odd.
if n is odd.
(xv) Let N = pa. qb. rc...... where p , q , r...... are distinct primes & a , b , c..... are natural numbers then:
(a) The total numbers of divisors of N including 1 & N is = (a + 1)(b + 1)(c + 1).....
(b) The sum of these divisors is = (p0 + p1 + p2 +.... + pa) (q0 + q1 + q2 +.... + qb) (r0 + r1 + r2 +.... + rc)....
(c) Number of ways in which N can be resolved as a product of two factors is = 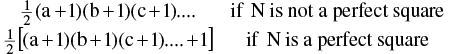
(d) Number of ways in which a composite number N can be resolved into two factors which are relatively prime (or coprime) to each other is equal to 2n−1 where n is the number of different prime factors in N.
(xvi) Grid Problems and tree diagrams.
DEARRANGEMENT : Number of ways in which n letters can be placed in n directed letters so that no letter goes into its own envelope is = n! 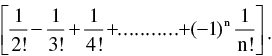
(xvii) Some times students find it difficult to decide whether a problem is on permutation or combination or both. Based on certain words / phrases occuring in the problem we can fairly decide its nature as per the following table :
|
73 videos|264 docs|91 tests
|
















