Important Complex Numbers & Quadratic Equations Formulas for JEE and NEET
Definition
- Complex numbers are defined as expressions of the form a + ib where a, b ∈ R & i = − 1. It is denoted by z i.e. z = a + ib. ‘a’ is called as real part of z (Re z) and ‘b’ is called as imaginary part of z (Im z).
- Every Complex Number Can be Regarded as
Purely real if b = 0
Purely imaginary if a = 0
Imaginary if b ≠ 0 - Note :
(a) The set R of real numbers is a proper subset of the Complex Numbers. Hence the Complete Number system is N ⊂ W ⊂ I ⊂ Q ⊂ R ⊂ C.
(b) Zero is both purely real as well as purely imaginary but not imaginary.
(c) i = −1 is called the imaginary unit. Also i2 = −1 ; i3 = −i ; i4 = 1 etc.
(d) √a √b = √ab only if atleast one of either a or b is non-negative.Conjugate Complex
If z = a + ib then its conjugate complex is obtained by changing the sign of its imaginary part & is denoted by .
.
(i) = 2 Re(z)
= 2 Re(z)
(ii) = 2i Im(z)
= 2i Im(z)
(iii) = a2 + b2 which is real
= a2 + b2 which is real
(iv) If z lies in the 1st quadrant then in the 4th quadrant and
in the 4th quadrant and 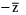 lies in the 2nd quadrant.
lies in the 2nd quadrant.Algebraic Operations
- The algebraic operations on complex numbers are similiar to those on real numbers treating i as a polynomial. Inequalities in complex numbers are not defined.
- There is no validity if we say that complex number is positive or negative.
e.g. z > 0, 4 + 2i < 2 + 4i are meaningless.Equality in Complex Numbers
- Two complex numbers z1 = a1 + ib1 & z2 = a2 + ib2 are equal if and only if their real & imaginary parts coincide.
Representation of Complex Numbers in Various Forms
(a) Cartesian Form (Geometric Representation): Every complex number z = x + iy can be represented by a point on the cartesian plane known as complex plane (Argand diagram) by the ordered pair (x, y). length OP is called modulus of the complex number denoted by |z| & θ is called the argument or amplitude
eg.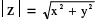
θ = tan−1(y/x) (angle made by OP with positive x−axis) - NOTE :
(i) |z| is always non negative. Unlike real numbers |z| =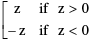 is not correct.
is not correct.
(ii) Argument of a complex number is a many valued function. If θ is the argument of a complex number then 2nπ + θ ; n ∈ I will also be the argument of that complex number. Any two arguments of a complex number differ by 2nπ.
(iii) The unique value of θ such that – π < θ ≤ π is called the principal value of the argument.
(iv) Unless otherwise stated, amp z implies principal value of the argument.
(v) By specifying the modulus & argument a complex number is defined completely. For the complex number 0 + 0 i the argument is not defined and this is the only complex number which is given by its modulus.
(vi) There exists a one-one correspondence between the points of the plane and the members of the set of complex numbers.(b) Trigonometric / Polar Representation - z = r (cos θ + i sin θ) where |z| = r; arg z = θ ;
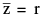 (cosθ − i sinθ)
(cosθ − i sinθ) - Note: cosθ + i sinθ is also written as CiS θ.Also
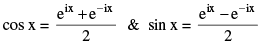 are known as Euler's identities.
are known as Euler's identities.
Properties of Conjugate/Moduli/Amplitude:
If z, z1, z2 ∈ C then;
(a)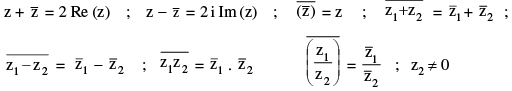
(b)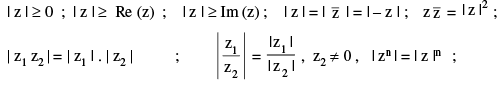
|z1 + z2|2 + |z1 – z2|2 = 2 [|z1|2 – |z2|2]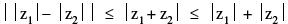 [TRIANGLE INEQUALITY]
[TRIANGLE INEQUALITY]
(c)
(i) amp (z1 . z2) = amp z1 + amp z2 + 2 kπ. k ∈ I
(ii) amp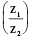 = amp z1 − amp z2 + 2 kπ ; k ∈ I
= amp z1 − amp z2 + 2 kπ ; k ∈ I
(iii) amp(zn) = n amp(z) + 2kπ.
where proper value of k must be chosen so that RHS lies in (−π, πVectorial Representation of Complex Numbers
Every complex number can be considered as if it is the position vector of that point. If the point P represents the complex number z then,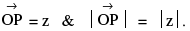 NOTE : (i) If
NOTE : (i) If 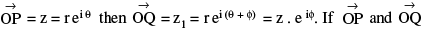 are of unequal magnitude then
are of unequal magnitude then 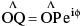
(ii) If A, B, C & D are four points representing the complex numbers z1, z2, z3 & z4 then(iii) If z1, z2, z3 are the vertices of an equilateral triangle where z0 is its circumcentre then (a)
Demoivre's Theorem
Statement : cos n θ + i sin n θ is the value or one of the values of (cos θ + i sin θ)n ¥ n ∈ Q. The theorem is very useful in determining the roots of any complex quantity
Note : Continued product of the roots of a complex quantity should be determined using theory of equations.
Cube Root of Unity
(i) The cube roots of unity are 1,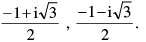
(ii) If w is one of the imaginary cube roots of unity then 1 + w + w2 = 0. In general 1 + wr + w2r = 0 ; where r ∈ I but is not the multiple of 3.
(iii) In polar form the cube roots of unity are :
cos 0 + i sin 0 ; cos 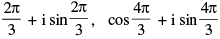
(iv) The three cube roots of unity when plotted on the argand plane constitute the verties of an equilateral triangle.
(v) The following factorisation should be remembered :
(a, b, c ∈ R & ω is the cube root of unity)
a3 − b3 = (a − b) (a − ωb) (a − ω2b) ; x2 + x + 1 = (x − ω) (x − ω2) ;
a3 + b3 = (a + b) (a + ωb) (a + ω2b) ; a3 + b3 + c3 − 3abc = (a + b + c) (a + ωb + ω2c) (a + ω2b + ωc)
nth Roots of Unity
If 1, α1, α2, α3 ..... αn − 1 are then, nth root of unity then :(i) They are in G.P. with common ratio ei(2π/n) &
(ii) 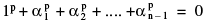 if p is not an integral multiple of n = n if p is an integral multiple of n
if p is not an integral multiple of n = n if p is an integral multiple of n
(iii) (1 − α1) (1 − α2) ...... (1 − αn − 1) = n & (1 + α1) (1 + α2) ....... (1 + αn − 1) = 0 if n is even and 1 if n is odd.
(iv) 1. α1. α2. α3 ......... αn − 1 = 1 or −1 according as n is odd or even.
Sum of Series
(i) cosθ + cos2θ + cos3θ + ..... + cosnθ = 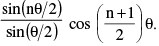
(ii) sinθ + sin2θ + sin3θ + ..... + sin n θ = 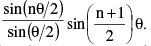 Note: If θ = (2π/n) then the sum of the above series vanishes.
Note: If θ = (2π/n) then the sum of the above series vanishes.
Straight Lines and Circles in terms of Complex Numbers
(A) If z1 & z2 are two complex numbers then the complex number z = 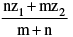 divides the joins of z1 & z2 in the ratio m : n.
divides the joins of z1 & z2 in the ratio m : n.Note: (i) If a, b, c are three real numbers such that az1 + bz2 + cz3 = 0 ; where a + b + c = 0 and a, b, c are not all simultaneously zero, then the complex numbers z1, z2 & z, are collinear.
(ii) If the vertices A, B, C of a ∆ represent the complex nos. z1, z2, z3 respectively, then :
(a) Centroid of the ∆ ABC = 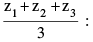
(b) Orthocentre of the ∆ ABC = 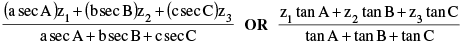
(c) Incentre of the ∆ ABC = (az1 + bz2 + cz3) ÷ (a + b + c).
(d) Circumcentre of the ∆ABC = : (Z1 sin 2A + Z2 sin 2B + Z3 sin 2C) ÷ (sin 2A + sin 2B + sin 2C) .
(B) amp(z) = θ is a ray emanating from the origin inclined at an angle θ to the x− axis.
(C) |z − a| = |z − b| is the perpendicular bisector of the line joining a to b.
(D) The equation of a line joining z1 & z2 is given by ;
z = z1 + t (z1 − z2) where t is a perameter.
(E) z = z1(1 + it) where t is a real parameter is a line through the point z1 & perpendicular to oz1.
(F) The equation of a line passing through z1 & z2 can be expressed in the determinant form as 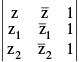 = 0. This is also the condition for three complex numbers to be collinear.
= 0. This is also the condition for three complex numbers to be collinear.
(G) Complex equation of a straight line through two given points z1 & z2 can be written as 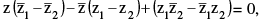 which on manipulating takes the form as
which on manipulating takes the form as 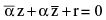 where r is real and α is a non zero complex constant.
where r is real and α is a non zero complex constant.
(H) The equation of circle having centre z0 & radius ρ is : |z − z0| = ρ or  which is of the form
which is of the form 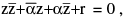 r is real centre − α & radius
r is real centre − α & radius 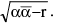 Circle will be real if
Circle will be real if 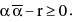
(I) The equation of the circle described on the line segment joining z1 & z2 as diameter is :
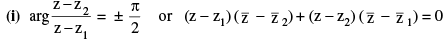
(J) Condition for four given points z1, z2, z3 & z4 to be concyclic is, the number 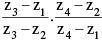 is real. Hence the equation of a circle through 3 non collinear points z1, z2 & z3 can be taken as
is real. Hence the equation of a circle through 3 non collinear points z1, z2 & z3 can be taken as 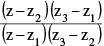 is real ⇒
is real ⇒ 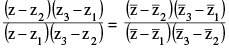
(a) Reflection points for a straight line: Two given points P & Q are the reflection points for a given straight line if the given line is the right bisector of the segment PQ. Note that the two points denoted by the complex numbers z1 & z2 will be the reflection points for the straight line 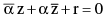 if and only if;
if and only if; 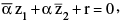 where r is real and α is non zero complex constant.
where r is real and α is non zero complex constant.
(b) Inverse points w.r.t. a circle :
Two points P & Q are said to be inverse w.r.t. a circle with centre 'O' and radius ρ, if :
(i) the point O, P, Q are collinear and on the same side of O.
(ii) OP.OQ = ρ2.
Note that the two points z1 & z2 will be the inverse points w.r.t. the circle 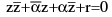 if and only if
if and only if 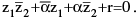
Ptolemy's Theorem
It states that the product of the lengths of the diagonals of a convex quadrilateral inscribed in a circle is equal to the sum of the lengths of the two pairs of its opposite sides.i.e. |z1 − z3| |z2 − z4| = |z1 − z2| |z3 − z4| + |z1 − z4| |z2 − z3|.
Logarithm of a Complex Quantity
(i)(ii) ii represents a set of positive real numbers given by 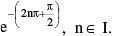
Theory Of Equations(Quadratic Equations)
The general form of a quadratic equation in x is, ax2 + bx + c = 0, where a, b, c ∈ R & a ≠ 0.
RESULTS :
1. The solution of the quadratic equation, ax2 + bx + c = 0 is given by x = 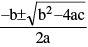
The expression b2 – 4ac = D is called the discriminant of the quadratic equation.
2. If α & β are the roots of the quadratic equation ax2 + bx + c = 0, then;
(i) α + β = – b/a
(ii) αβ = c/a
(iii) α – β = √D/a.
NATURE OF ROOTS:
(A) Consider the quadratic equation ax2 + bx + c = 0 where a, b, c ∈ R & a≠ 0 then
(i) D > 0 ⇔ roots are real & distinct (unequal).
(ii) D = 0 ⇔ roots are real & coincident (equal).
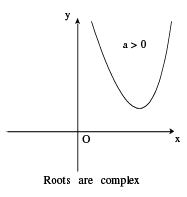
(iii) D < 0 ⇔ roots are imaginary.
(iv) If p + i q is one root of a quadratic equation, then the other must be the conjugate p − i q & vice versa. (p, q ∈ R & i =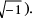
(B) Consider the quadratic equation ax2 + bx + c = 0 where a, b, c ∈ Q & a ≠ 0 then;
(i) If D > 0 & is a perfect square, then roots are rational & unequal.
(ii) If α = p + q is one root in this case, (where p is rational & √q is a surd) then the other root must be the conjugate of it i.e. β = p − √q & vice versa.
4. A quadratic equation whose roots are α & β is (x − α)(x − β) = 0 i.e. x2 − (α + β) x + αβ = 0 i.e. x2 − (sum of roots) x + product of roots = 0.
5. Remember that a quadratic equation cannot have three different roots & if it has, it becomes an identity.
6. Consider the quadratic expression, y = ax2 + bx + c, a ≠ 0 & a, b, c ∈ R then
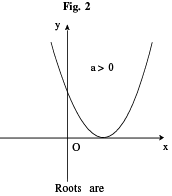
(i) The graph between x, y is always a parabola. If a > 0 then the shape of the parabola is concave upwards & if a < 0 then the shape of the parabola is concave downwards.
(ii) ∀ x ∈ R, y > 0 only if a > 0 & b² − 4ac < 0 (figure 3).
(iii) ∀ x ∈ R, y < 0 only if a < 0 & b² − 4ac < 0 (figure 6).
Carefully go through the 6 different shapes of the parabola given below.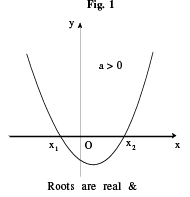
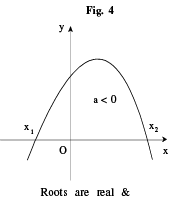
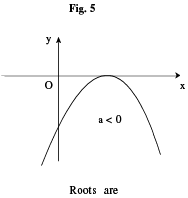
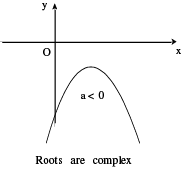
SOLUTION OF QUADRATIC INEQUALITIES:
ax2 + bx + c > 0 (a ≠ 0).
(i) If D > 0, then the equation ax2 + bx + c = 0 has two different roots x1 < x2.
Then a > 0 ⇒ x ∈ (−∞, x1) ∪ (x2, ∞)
a < 0 ⇒ x ∈ (x1, x2)
(ii) If D = 0, then roots are equal, i.e. x1 = x2.
In that case a > 0 ⇒ x ∈ (−∞, x1) ∪ (x1, ∞)
a < 0 ⇒ x ∈ φ
(iii) Inequalities of the form 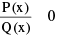 can be quickly solved using the method of intervals.
can be quickly solved using the method of intervals.
MAXIMUM & MINIMUM VALUE
Maximum and Minimum value of y = ax² + bx + c occurs at x = − (b/2a) according as ; a < 0 or a > 0. 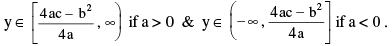
COMMON ROOTS OF 2 QUADRATIC EQUATIONS [ONLY ONE COMMON ROOT]:
Let α be the common root of ax2 + bx + c = 0 & a′x2 + b′x + c′ = 0 Therefore a α2 + bα + c = 0; a′α2 + b′α + c′ = 0. By Cramer’s Rule 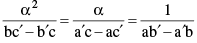 Therefore, α =
Therefore, α =
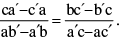 So the condition for a common root is (ca′ − c′a)2 = (ab′ − a′b)(bc′ − b′c).
So the condition for a common root is (ca′ − c′a)2 = (ab′ − a′b)(bc′ − b′c).
The condition that a quadratic function f (x, y) = ax2 + 2 hxy + by2 + 2gx + 2 fy + c may be resolved into two linear factors is that ;
abc + 2 fgh − af2 − bg2 − ch2 = 0 OR 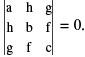
Theory of Equations
If α1, α2, α3, ......αn are the roots of the equation; f(x) = a0xn + a1xn-1 + a2xn-2 + .... + an-1x + an = 0 where a0, a1, .... an are all real & a0 ≠ 0 then, ∑α1 = 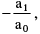
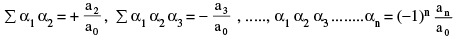 Note :
Note :
(i) If α is a root of the equation f(x) = 0, then the polynomial f(x) is exactly divisible by (x − α) or (x − α) is a factor of f(x) and conversely .
(ii) Every equation of nth degree (n ≥ 1) has exactly n roots & if the equation has more than n roots, it is an identity.
(iii) If the coefficients of the equation f(x) = 0 are all real and α + iβ is its root, then α − iβ is also a root. i.e. imaginary roots occur in conjugate pairs.
(iv) If the coefficients in the equation are all rational & α + √β is one of its roots, then α − √β is also a root where α, β ∈ Q & β is not a perfect square.
(v) If there be any two real numbers 'a' & 'b' such that f(a) & f(b) are of opposite signs, then f(x) = 0 must have atleast one real root between 'a' and 'b'.
(vi) Every equation f(x) = 0 of degree odd has atleast one real root of a sign opposite to that of its last term.
LOCATION OF ROOTS :
Let f (x) = ax2 + bx + c, where a > 0 & a, b, c ∈ R.
(i) Conditions for both the roots of f(x) = 0 to be greater than a specified number ‘d’ are b2 − 4ac ≥ 0; f (d) > 0 & (− b/2a) > d.
(ii) Conditions for both roots of f (x) = 0 to lie on either side of the number ‘d’ (in other words the number ‘d’ lies between the roots of f (x) = 0) is f (d) < 0.
(iii) Conditions for exactly one root of f (x) = 0 to lie in the interval (d, e) i.e. d < x < e are b2 − 4ac > 0 & f (d). f (e) < 0.
(iv) Conditions that both roots of f (x) = 0 to be confined between the numbers p & q are (p < q). b2 − 4ac ≥ 0; f (p) > 0; f (q) > 0 & p < (− b/2a) < q.
Logarithmic Inequalities
(i) For a > 1 the inequality 0 < x < y & loga x < loga y are equivalent.
(ii) For 0 < a < 1 the inequality 0 < x < y & loga x > loga y are equivalent.
(iii) If a > 1 then loga x < p ⇒ 0 < x < ap
(iv) If a > 1 then loga x > p ⇒ x > ap
(v) If 0 < a < 1 then loga x < p ⇒ x > ap
(vi) If 0 < a < 1 then loga x > p ⇒ 0 < x < ap
|
172 videos|503 docs|154 tests
|
FAQs on Important Complex Numbers & Quadratic Equations Formulas for JEE and NEET
| 1. What are the different forms in which complex numbers can be represented? |  |
| 2. How can complex numbers be used to represent straight lines and circles? |  |
| 3. What is the cube root of unity and how is it related to complex numbers? |  |
| 4. How can complex numbers be used to find the nth roots of unity? |  |
| 5. How can algebraic operations be performed on complex numbers? |  |

















