Important Binomial Theorem Formulas for JEE and NEET
1. BINOMIAL THEOREM :
The formula by which any positive integral power of a binomial expression can be expanded in the form of a series is known as BINOMIAL THEOREM. If x, y ∈ R and n ∈ N, then;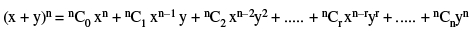

This theorem can be proved by Induction.
OBSERVATIONS :
(i) The number of terms in the expansion is (n + 1) i.e. one or more than the index .
(ii) The sum of the indices of x & y in each term is n
(iii) The binomial coefficients of the terms nC0, nC1 .... equidistant from the beginning and the end are equal.
2. IMPORTANT TERMS IN THE BINOMIAL EXPANSION ARE:
(i) General term
(ii) Middle term
(iii)Term independent of x &
(iv) Numerically greatest term
(i) The general term or the (r + 1)th term in the expansion of (x + y)n is given by; Tr+1 = nCr xn−r . yr
(ii) The middle term(s) is the expansion of (x + y)n is (are) :
(a) If n is even, there is only one middle term which is given by;
T(n+2)/2 = nCn/2 . xn/2 . yn/2
(b) If n is odd, there are two middle terms which are:
T(n+1)/2 & T[(n+1)/2]+1
(iii) Term independent of x contains no x ; Hence find the value of r for which the exponent of x is zero.
(iv) To find the Numerically greatest term is the expansion of (1 + x) n, n ∈ N find 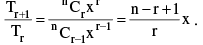 Put the absolute value of x & find the value of r Consistent with the inequality
Put the absolute value of x & find the value of r Consistent with the inequality 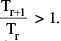
Note that the Numerically greatest term in the expansion of (1 − x)n, x > 0, n ∈ N is the same as the greatest term in (1 + x)n.
3. If 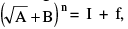 where I & n are positive integers, n being odd and 0 < f < 1, then (I + f). f = Kn where A − B2 = K > 0 &
where I & n are positive integers, n being odd and 0 < f < 1, then (I + f). f = Kn where A − B2 = K > 0 & 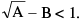
If n is an even integer, then (I + f) (1 − f) = Kn.
4. BINOMIAL COEFFICIENTS :
(i) C0 + C1 + C2 + ....... + Cn = 2n
(ii) C0 + C2 + C4 + ....... = C1 + C3 + C5 + ....... = 2n−1
(iii) 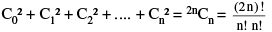
(iv)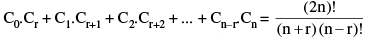
REMEMBER : (i) (2n)! = 2n . n! [1. 3. 5 ...... (2n − 1)]
5. BINOMIAL THEOREM FOR NEGATIVE OR FRACTIONAL INDICES
If n ∈ Q, then (1 + x)n = 
Note : (i) When the index n is a positive integer the number of terms in the expansion of (1 + x)n is finite i.e. (n + 1) & the coefficient of successive terms are:
nC0 , nC1 , nC2 , nC3 ..... nCn
(ii) When the index is other than a positive integer such as negative integer or fraction, the number of terms in the expansion of (1 + x)n is infinite and the symbol nCr cannot be used to denote the Coefficient of the general term.
(iii) Following expansion should be remembered (|x| < 1).
(a) (1 + x)−1 = 1 − x + x2 − x3 + x4 − .... ∞
(b) (1 − x)−1 = 1 + x + x2 + x3 + x4 + .... ∞
(c) (1 + x)−2 = 1 − 2x + 3x2 − 4x3 + .... ∞
(d) (1 − x)−2 = 1 + 2x + 3x2 + 4x3 + ..... ∞
(iv) The expansions in ascending powers of x are only valid if x is ‘small’. If x is large i.e. | x | > 1 then we may find it convinient to expand in powers of (1/x), which then will be small.
6. APPROXIMATIONS : (1 + x)n = 1 + nx + 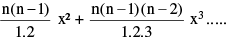
If x < 1, the terms of the above expansion go on decreasing and if x be very small, a stage may be reached when we may neglect the terms containing higher powers of x in the expansion. Thus, if x be so small that its squares and higher powers may be neglected then (1 + x)n = 1 + nx, approximately. This is an approximate value of (1 + x)n.
7. EXPONENTIAL SERIES :
(i) 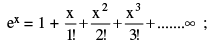 where x may be any real or complex & e =
where x may be any real or complex & e =
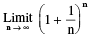
(ii) 
Note :
(a) 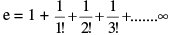
(b) e is an irrational number lying between 2.7 & 2.8. Its value correct upto 10 places of decimal is 2.7182818284.
(c) 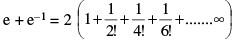
(d) 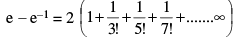
(e) Logarithms to the base ‘e’ are known as the Napierian system, so named after Napier, their inventor. They are also called Natural Logarithm.
8. LOGARITHMIC SERIES :
(i) 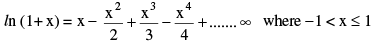
(ii) 
(iii) 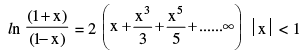
REMEMBER :
(a) 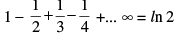
(b) eln x = x
(c) ln 2 = 0.693
(d) ln 10 = 2.303
|
75 videos|238 docs|91 tests
|
FAQs on Important Binomial Theorem Formulas for JEE and NEET
| 1. What is the Binomial Theorem? |  |
| 2. How is the Binomial Theorem used in mathematics? |  |
| 3. What is the general form of the Binomial Theorem? |  |
| 4. How do you calculate the binomial coefficient in the Binomial Theorem? |  |
| 5. Can the Binomial Theorem be used for negative exponents? |  |

|
Explore Courses for Commerce exam
|

|

















