Q1: At the current basic feasible solution (bfs) 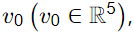 the simplex method yields the following form of a linear programming problem in standard form.
the simplex method yields the following form of a linear programming problem in standard form.
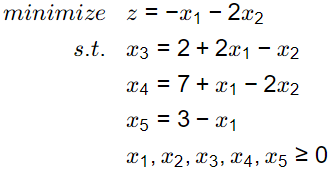 Here the objective function is written as a function of the non-basic variables. If the simplex method moves to the adjacent bfs
Here the objective function is written as a function of the non-basic variables. If the simplex method moves to the adjacent bfs 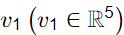 that best improves the objective function, which of the following represents the objective function at v1, assuming that the objective function is written in the same matter as above? [GATE ME 2024]
that best improves the objective function, which of the following represents the objective function at v1, assuming that the objective function is written in the same matter as above? [GATE ME 2024]
(a) z = −4 − 5x1 + 2x3
(b) z = −3 + x5 − 2x2
(c) z = −4 − 5x1 − 2x4
(d) z = −6 − 5x1 + 2x3
Ans: (a)
z = -x₁ - 2x₂ ...(A)
x₃ = 2 + 2x₁ - x₂ ...(i)
x₄ = 7 + x₁ - 2x₂ ...(ii)
x₅ = 3 - x ...(iii)
and x₁, x₂, x₃, x₄, x₅ ≥ 0
From eq. (i):
x₂ = 2 + 2x₁ - x₃
Putting this value in the objective function eq. (A):
z = -x₁ - 2(2 + 2x₁ - x₃)
z = -4 - 5x₁ + 2x₃
From equation (ii):
x₁ = x₄ + 2x₂ − 7
Substitute this value in equation (A):
z = − (x₄ + 2x₂ − 7) − 2x₂
= 7 − 4x₂ − x₄
From equation (iii):
x₁ = 3 − x₅
Substitute this value in equation (A):
z = − (3 − x₅) − 2x₂
= x₅ − 3 − 2x₂
(A) and (B) both are correct but question type is mcq so go for option (A).
Q1: Which one of the options given represents the feasible region of the linear programming model: [GATE ME 2023]
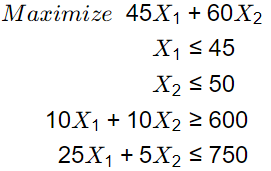
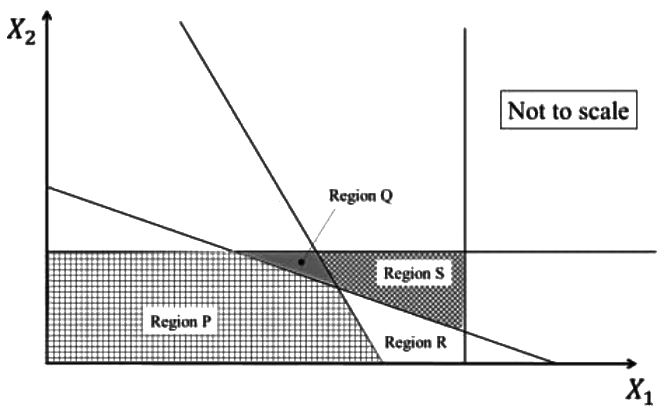 (a) Region P
(a) Region P
(b) Region Q
(c) Region R
(d) Region S
Ans: (b)
x₁ = 45 ... (i)
x₂ = 50 ... (ii)
10x₁ + 10x₂ = 600
or x₁ + x₂ = 60 ... (iii)
25x₁ + 5x₂ = 750
or 5x₁ + x₂ = 150 ... (iv)
By drawing the curve, we get 3 values of x₁ and x₂ as (10, 50), (20, 50), (22.5, 37.5).
So, Zmax = 45x₁ + 60x₂ for (10, 50)
Zmax = 45 × 10 + 60 × 50 = 4450
For (20, 50)
Zmax = 45 × 20 + 50 × 60 = 3900
For (22.5, 37.5)
Zmax = 45 × 22.5 + 60 × 37.5 = 3262.5
So, Zmax = 3900 for (x₁, x₂) = (20, 50)
Q1: A manufacturing unit produces two products P1 and P2. For each piece of P1 an P2, the table below provides quantities of materials M1, M2, and M3 required, and also the profit earned. The maximum quantity available per day for M1, M2 and M3 is also provided. The maximum possible profit per day is Rs __________. [GATE ME 2022 SET-2]
 (a) 5000
(a) 5000
(b) 4000
(c) 3000
(d) 6000
Ans: (b)
Let,
x₁ = Number of units of product P₁
x₂ = Number of units of product P₂
Max, Z = 150x₁ + 100x₂
Subject to:
2x₁ + 3x₂ ≤ 70
2x₁ + 3x₂ ≤ 50
2x₂ ≤ 40
x₁ ≥ 0, x₂ ≥ 0
Point B: Intersection of
2x₁ + 3x₂ ≤ 70
2x₂ ≤ 40
x₂ = 20, x₁ = 5
Point C: Intersection of
2x₁ + 3x₂ ≤ 70
2x₁ + x₂ ≤ 50
By solving 2x₂ = 20
⇒ x₂ = 10, x₁ = 20
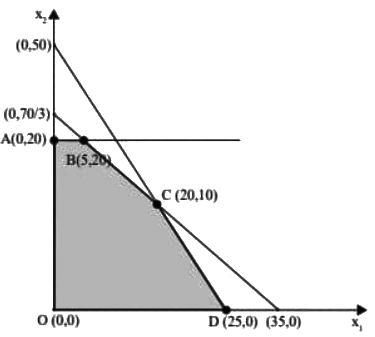
Zₘₐₓ = 150x₁ + 100x₂
Z|(A(0,20)) = 150(0) + 100(20) = 2000
Z|(B(5,20)) = 150(5) + 100(20) = 2750
Z|(C(20,10)) = 150(20) + 100(10) = 4000
Z|(D(25,0)) = 150(25) + 100(0) = 3750
⇒ x₁ = 20, x₂ = 10
Zₘₐₓ = 4000
Q2: In a linear programming problem, if a resource is not fully utilized, the shadow price of that resource is [GATE ME 2022 SET-1]
(a) positive
(b) negative
(c) zero
(d) infinity
Ans: (c)
In a Linear programming problem if a resource is not fully utilized. The shadow price or dual price of the particular resource is zero.
Q1: Two business owners Shveta and Ashok run their businesses in two different states. Each of them, independent of the other, produces two products A and B, sells them at Rs. 2,000 per kg and Rs, 3,000 per kg, respectively, and uses Linear Programming to determine the optimal quantity of A and B to maximize their respective daily revenue. Their constraints are as follows: i) for each business owner, the production process is such that the daily production of A has to be at least as much as B, and the upper limit for production of B is 10 kg per day, and ii) the respective state regulations restrict Shveta?s production of A to less than 20 kg per day and Ashok's production of A to less than 15 kg per day. The demand of both A and B in both the states is very high and everything produced is sold.
The absolute value of the difference in daily (optimal) revenue of Shveta and Ashok is ________ thousand Rupees (round off to 2 decimal places) [GATE ME 2020 SET-1]
Ans: 9.9 to 10.1
Maximum z = 2000x₁ + 3000x₂
A → x₁ units, x₁ ≥ x₂
B → x₂ units, x₂ ≥ 10
x₂ < 20
x₁ < 15
Shveta’s Profit = Rs. 70,000 at (20, 10)
Ashok’s Profit = Rs. 60,000 at (15, 10)
Difference = Rs. 10,000
Question for GATE Past Year Questions: Linear Programming
Try yourself:The manufacturer can make a maximum profit of Rs.
[2011]
Question for GATE Past Year Questions: Linear Programming
Try yourself:A company produces two types of toys : P and Q. Production time of Q is twice that of P and the company has a maximum of 2000 time units per day. The supply of raw material is just sufficient to produce 1500 toys (of any type) per day. Toy type Q requires an electric switch which is available @ 600 pieces per day only.The company makes a profit of Rs. 3 and Rs. 5 on type P and Q respectively. For maximizationof profits, the daily production quantities of P and Q toys should respectively be
[2004]
Explanation
Zmax = 3P +5Q
subject to
P+ 2Q ≤ 2000
P+Q ≤ 1500
Q ≤ 600
P,Q ≥ 0
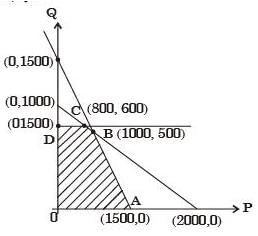
Feasible solution (O A B C D) Since At point A (1500,0) Z = 3 × 1500 + 5 × 0 = 4500
At Point B (1000, 500) Z = 3 × 1000 + 5 × 500 = 5500
At point C (800, 600) Z = 3 × 800 + 5 × 600 = 5400
At Point O (0, 600) Z = 3 × 0 + 5 × 600 = 3000
Hence Z in maximum at B (1000,500) P = 1000 units Q = 500 units
Report a problem
Question for GATE Past Year Questions: Linear Programming
Try yourself: Simplex method of solving linear programming problem uses
[2010]
Question for GATE Past Year Questions: Linear Programming
Try yourself:The dual for the LP in Q. 21 is
[2008]
Question for GATE Past Year Questions: Linear Programming
Try yourself:After introducing slack variables s and t, the initial basic feasible solution is represented by the table below (basic variables are s = 6 and t = 6, and the objective function value is 0).

After some simplex iterations, the following table is obtained

From this, one can conclude that
[2008]
Explanation
z = 4x + 6y
3x + 2y ≤ 6
2x + 3y ≤ 6
x, y > 0
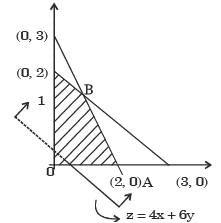
Feasible region (O–A–B–C–0) Since, Slope of objective function is equal to the slope of constraint Hence LPP has multiple optimal solution
At B (6/5, 6/5)
Z = 12
At C (0,2)
Z = 12
Report a problem
Question for GATE Past Year Questions: Linear Programming
Try yourself:For the standard transportation linear program with m sources and n destinations and total supply equaling total demand, an optimal solution (lowest cost) with the smallest number of non-zero xij values (amounts from source i to destination j) is desired. The best upper bound for this number is
[2008]
Explanation
In such an L .P.P, m × n variables are th ere an d m + n equations/constraints are there (satisfying the demand-supply requirements). But one constraint is removed as total supply equals total demand. The best upper bound xij values is (m + n � 1).
Report a problem
Question for GATE Past Year Questions: Linear Programming
Try yourself:For the linear programming problem:
Maximize z = 3x1 + 2x2
Subject to –2x1 + 3x2 < 9x1 – 5x2 > – 20x1, x2 > 0
The above problem has
[2016]
Explanation
Maximize Z= 3X1 + 2X2
Subject to
-2X1 + 3X2 ≤ 9
X1 - 5X2 ≥ 20
XP X2 ≥ 0

The LPP is unbounded.
Report a problem
Question for GATE Past Year Questions: Linear Programming
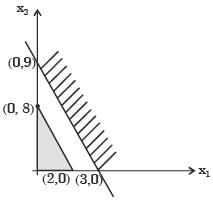
Try yourself:Maximize z = 15x1 + 20x2
Subject to 12x1 + 4x2 > 36
12x1 + 6x2 > 24 x1,
x2 > 0
The above linear programming problem has
Explanation
zmax = 16x1 + 20x2
12x1 + 4x2 ≥36
12x1 + 6x2 ≥24 x1
x2 ≥ 0
Report a problem
Question for GATE Past Year Questions: Linear Programming
Try yourself:A linear programming problem is shown below:
Maximise 3x + 7y
Subjeot to 3x + 7y < 10
4x + 6y < 8 x, y > 0
[2013]
Explanation
z = 3x + 7y Constraints 3x + 7y ≤ 10 4x + 6y < 8; x, y ≥ 0 Corresponding equations 3x + 7y = 10; 4x + 6y =8

A (0, 4/3) z = 9.23 B (2, 0) z = 6 Thus, exactly one optimal solution.
Hence, the correct option is (b).
Report a problem
Question for GATE Past Year Questions: Linear Programming
Try yourself:The manufacturer can make a maximum profit of Rs.
[2011]
Explanation
z = 2000 P1 + 3000 P2
Subjected to
3P1 +2P2 ≤ 90
P1 + 2P2 ≤ 100
P1, P2 ≥ 0

At point A (30, 0) Z = 30 × 2000 × 3000 × 0 = 6000
At point B (0, 45) Z = 2000× 0 + 3000 × 45 = 135000
Hence Maximum Profit
[Zmax = 135000]
Report a problem
Question for GATE Past Year Questions: Linear Programming
Try yourself:One unit of product P1 requires 3 kg of resource R1 and 1 kg resource R2. One unit of product P2 requires 2 kg of resource R1 and 2 kg of resource R2. The profits per unit by selling product P1 and P2 and Rs. 12000 and Rs 3000 respectively. The manufacturer has 90 kg of resource R1, and 100 kg of resource R2.
The unit worth of resource R2, i.e. dual price of resource R2 in Rs per kg is
[2011]
Explanation
Because second constraint is redundant in nature. Therefore, resource R2 has no effect on the feasible solution.
Report a problem
Question for GATE Past Year Questions: Linear Programming
Try yourself:Consider the following Linear Programming Problem (LPP):
Maximize z = 3x1 + 2x2,
Subject to x1 < 4 x2 < = 6
3x1 + 2x2 < 18
x1 > 0, x2 > 0
[2009]
Explanation
z= 3 × 1 + 2 × 2
x1 ≤ 4
x2 ≤ 6
3x1 + 2x2 ≤ 18
x1,x2 ≥ 0

Report a problem
Question for GATE Past Year Questions: Linear Programming
Try yourself:A firm is required to procure three items (P, Q, and R). The prices quoted for these items (in Rs.) by suppliers S1, S2 and S3 are given in table. The management policy requires that each item has to be supplied by only one supplier and one supplier supply only one item.The minimum total cost (in Rs.) of procurement to the firm is
[2006]
Question for GATE Past Year Questions: Linear Programming
Try yourself:Let Y1 and Y2 be the decision variables of the dual and v1 and v2 be the slack variables of the dual of the given linear programming problem.The optimum dual variables are
[2005]
Explanation
The optimal dual variables are V1 & V2 .
Report a problem
Question for GATE Past Year Questions: Linear Programming
Try yourself:If an additional constraint X1 + X2 < 5 is added, the optimal solution is
[2005]
Explanation
Max z = x1 + x2
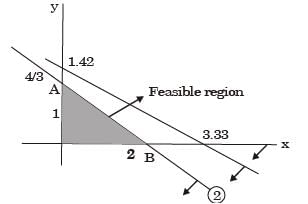
As feasibly region remains the same solution remains the same (4/3, 4/3).
Hence, the correct option is (b).
Report a problem
Question for GATE Past Year Questions: Linear Programming
Try yourself:A company has two factories S1, S2 and two warehouses D1, D2. The supplies from S1 and S2 are 50 and 40 units respectively. Warehouse D1 requires a minimum of 20 units and a maximum of 40 units. Warehouse D2 requires a minimum of 20 units and, over and above, it can take as much as can be supplied. A balanced transportation problem is to be formulated for the above situation. The number of supply points, the number of demand points, and the total supply (or total demand) in the balanced transportation problem respectively are
[2005]
Explanation

Total no of supply point
⇒ m + n – 1
⇒ 2 + 2 – 1
⇒ 3
Total no of Demand point = 4
(x11, x12, x21, x22)
Total supply = Total Demand Þ 90 units
Report a problem
Question for GATE Past Year Questions: Linear Programming
Try yourself:A component can be produced by any of the four processes, I, II, III and IV. Process I has fixed cost of Rs. 20 and variable cost of Rs. 3 per piece.Process II has a fixed cost of Rs. 50 and variable cost of Rs. 1 per piece. Process III has a fixed cost of Rs. 40.00 and variable cost of Rs. 2 per piece. Process IV has fixed cost of Rs. 10 and Variable cost Rs. 4 per piece. If company wishes to produce 100 pieces of the component, from economic point of view it should choose
[2005 : 2 Marks]
Explanation

Total cost = Fixed Cost (FC) + Number of piece (n) × Variable Cost per piece (VC) TC = FC + (n) x V.C
For I
TCI = 20+ (100) 3 = 320
For II
TCII = 50 + (100) 1 = 150
For III
TCIII = 40 + 100 (2) = 240
ForIV
TCIV = 10 + 100 (4) = 410
So from economical point of view, one should chose process II
Report a problem
Question for GATE Past Year Questions: Linear Programming
Try yourself:A manufacturer produces two types of products, 1 and 2, at production levels of x1 and x2 respectively. The profit is given is 2x1 + 5x2. The production constraints are:
x1 + 3x2 < 40
3x1 + x2 < 24
x1 + x2 < 10
x1 > 0 x2 > 0
The maximum profit which can meet the constraints is
[2003]
Explanation

Feasible Region (0– A – B – C– 0) At point (A) 0, 10) Z = 2 (0) + 5 (10) = 50
At point B (7,3) Z = 2(7) + 5(3) = 2y At point C (8, 0) Z = 2(16) + 5(0) = (16) 2
⇒32
Hence maximum profit is Zmax = 50
No correct option is given.
Report a problem
Question for GATE Past Year Questions: Linear Programming
Try yourself:If at the optimum in a linear programming problem, a dual variable corresponding to a particular primal constraint is zero, then it means that
[1996]
Question for GATE Past Year Questions: Linear Programming
Try yourself:In an assembly line for assembling toys, five workers are assigned tasks which take times of 10, 8, 6, 9 and 10 minutes respectively. The balance delay for line is
[1996]
Explanation
Assuming cycle time = 10 + 8 + 6 + 9 + 10 = 43
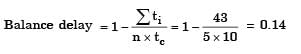 = 14%
= 14%
Report a problem
 the simplex method yields the following form of a linear programming problem in standard form.
the simplex method yields the following form of a linear programming problem in standard form. 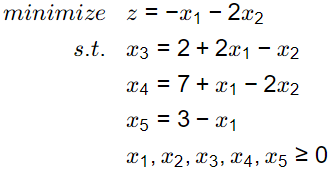 Here the objective function is written as a function of the non-basic variables. If the simplex method moves to the adjacent bfs
Here the objective function is written as a function of the non-basic variables. If the simplex method moves to the adjacent bfs 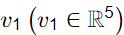 that best improves the objective function, which of the following represents the objective function at v1, assuming that the objective function is written in the same matter as above? [GATE ME 2024]
that best improves the objective function, which of the following represents the objective function at v1, assuming that the objective function is written in the same matter as above? [GATE ME 2024]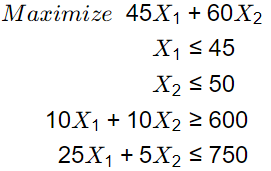
 (a) Region P
(a) Region P (a) 5000
(a) 5000



















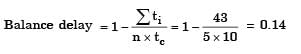 = 14%
= 14%














