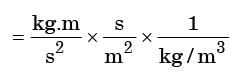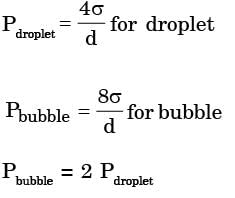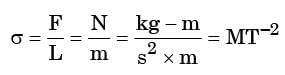GATE Past Year Questions: Fluid Properties | Fluid Mechanics for Mechanical Engineering PDF Download
Q1: A cube of side 100 mm is placed at the bottom of an empty container on one of its faces. The density of the material of the cube is 800 kg/m3. Liquid of density 1000 kg/m3 is now poured into the container. The minimum height to which the liquid needs to be poured into the container for the cube to just lift up is _____ mm. (2019 Set -1)
Ans: 80
Sol: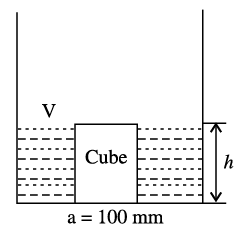
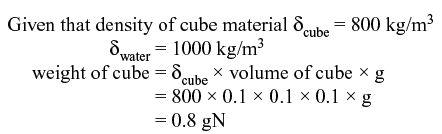
To just lift the cube
weight of cube = bouyamey force = weight of liquid displaced
= liquid × volume of liquid × g
= 1000 × 0.1 × 0.1 × h × g = 10 hg
where h = height of water pound By equating weight of cube = bouyamey force
0.8g = 10 hg
Q2: Two immiscible, incompressible, viscous fluids having same densities but different viscosities are contained between two infinite horizontal parallel plates, 2 m apart as shown below. The bottom place is fixed and the upper plate moves to the right with a constant velocity of 3 m/s. With the assumptions of Newtonian fluid, steady, and fully developed laminar flow with zero pressure gradient in all directions, the momentum equations simplify to 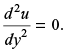
If the dynamic viscosity of the lower fluid, μ2, is twice that of fluid, μ1, then the velocity at the interface (round off to two decimal places) is ______ m/s. (2019 Set - 1)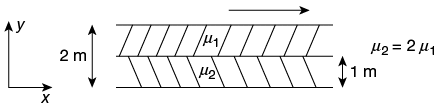 Ans: 1
Ans: 1
Sol: 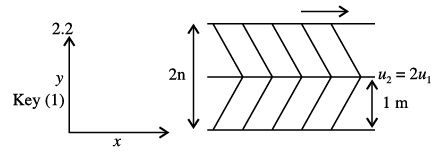
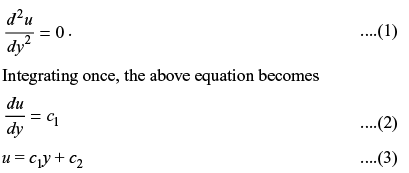
from equation (3) we can say that velocity is linearly varying so shear stress will be constant at the interface of two viscous fluids. i.e. shear stress at y = 1 m, from fixed plate is equal to shear stress at 1 m from moving plate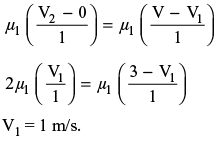
Q3: A solid block of 2.0 kg mass slides steadily at a velocity V along a vertical wall as shown in the figure below. A thin oil film of thickness h = 0.15 mm provides lubrication between the block and the wall. The surface area of the face of the block in contact with the oil film is 0.04 m2. The velocity distribution within the oil film gap is linear as shown in the figure. Take dynamic viscosity of oil as 7.10–3 Pa-s and acceleration due to gravity as 10 ms2. Neglect weight of the oil. The terminal velocity V(in m s) of the block is ______ (correct to one decimal place). (2018 Set - 1)
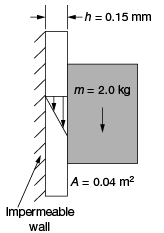
Ans: 10.714
Sol:
Mass m = 2 kg
Acceleration g = 10 m/s2
Height h = 15 mm
Terminal velocity V = ?
We know that terminal velocity is constant velocity, therefore net acceleration is zero.
Shear force due to oil film = weight of block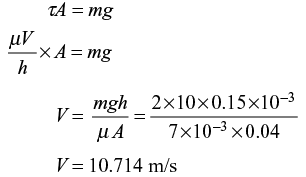
Hence, the correct answer is 10.714
Q4: A flat plate of width L = 1 m is pushed down with a velocity U = 0.01 m/s towards a wall resulting in the drainage of the fluid between the plate and the wall as shown in the figure. Assume two-dimensional incompressible flow and that the plate remains parallel to the wall. The average velocity, Uavg of the fluid (in m/s) draining out at the instant shown in the figure is _______ (correct to three decimal places). (2018- Set- 1)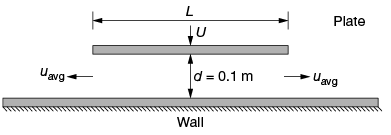
Ans: 0.05
Sol: Width of flat plate L = 1 m
Velocity of flat plate U = 0.01 m/s
Distance between flat plate and wall d = 0.1 m
If we assume the length of plate be Z
Rates of mass through plate = Rate of mass displaced between plates and wall.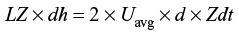
Where Uavg is the average velocity of the fluid (in m/s) draining out at the instant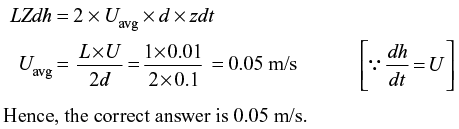
Q5: Consider fluid flow between two infinite horizontal plates which are parallel (the gap between them being 50 mm). The top plate is sliding parallel to the stationary bottom plate at a speed of 3 m/s. The flow between the plates is solely due to the motion of the top plate. The force per unit area (magnitude) required to maintain the bottom plate stationary is ______ N/m2.
Viscosity of the fluid µ = 0.44 kg/m-s and density ρ = 88 kg/m3. (2016 Set- 2)
Ans: 26.4
Sol: 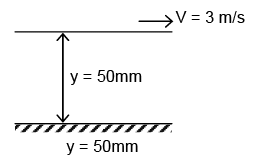
Viscosity of the fluid μ=0.44 kg/m⋅s
Density of fluid ρ=88 kg/m3
The force per unit area (magnitude) required to maintain the bottom plate stationary will be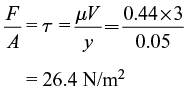
Hence, the correct answer is 26.4.
Q6: In a simple concentric shaft-bearing arrangement, the lubricant flows in the 2 mm gap between the shaft and the bearing. The flow may be assumed to be a plane couette flow with zero pressure gradients. The diameter of the shaft is 100 mm and its tangential speed is 10 m/s. The dynamic viscosity of the lubricant is 0.1 kg/m ∙ s. The frictional resisting force (in Newton) per 100 mm length of the bearing is _____ (2014 Set - 1)
Ans: 15.7
Sol: 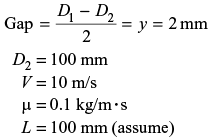
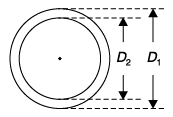
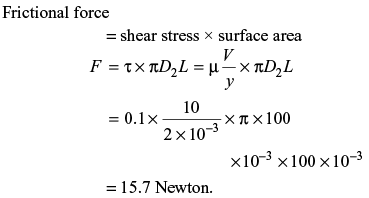
Q7: The difference in pressure (in N/m2) across an air bubble of diameter 0.001 m immersed in water (surface tension = 0.072 N/m) is _____ (2014 - Set -2)
Ans: 576
Sol: Difference in pressure across an air bubble
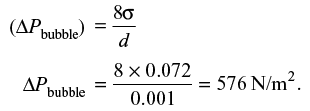
Q8: A lightly loaded full journal bearing has journal diameter of 50 mm, bush bore of 50.50 mm and bush length of 20 mm. If rotational speed of journal is 1200 rpm and average viscosity of liquid lubricant is 0.3 Pa-sec, the power loss (in Watt) will be (2010)
(a) 37
(b) 74
(c) 118
(d) 237
Ans: (a)
Sol:
D1 = 50.5 mm; D2 = 50 mm
L = 20 mm; N = 1200 rpm
μ = 0.3 Pa-sec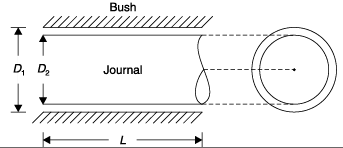
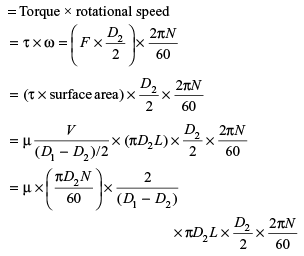
After putting values,
Power loss = 37 Watts
Hence, the correct option is (a)
[2001]
[1999]
[2016 Set-2]
[2006]
[1999]
[1996]
[1996]
[1995]
|
56 videos|146 docs|75 tests
|
FAQs on GATE Past Year Questions: Fluid Properties - Fluid Mechanics for Mechanical Engineering
| 1. What are the key properties of fluids? |  |
| 2. How does temperature affect the properties of fluids? |  |
| 3. What is the significance of viscosity in fluid properties? |  |
| 4. How does pressure impact the properties of fluids? |  |
| 5. Why is understanding fluid properties important in various engineering applications? |  |