GATE Past Year Questions: Principal Stress & Strain | Strength of Materials (SOM) - Mechanical Engineering PDF Download
Q1: The figure shows a thin cylinder pressure vessel constructed by welding plates together along a line that makes an angle α = 60º with the horizontal. The closed vessel has a wall thickness of 10 mm and diameter of 2m. When subjected to an internal pressure of 200kPa, the magnitude of the normal stress acting on the weld is ______ MPa (rounded off to 1 decimal place). (2024)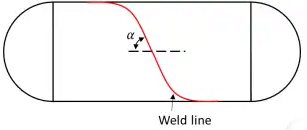 (a) 12.5
(a) 12.5
(b) 5.5
(c) 18.6
(d) 22.6
Ans: (a)
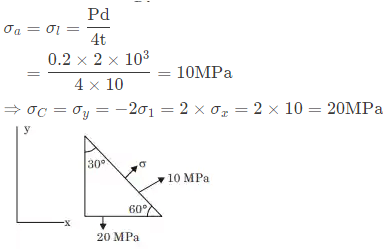
Sol: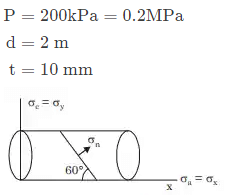
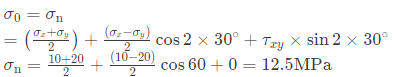
Q2: Ignoring the small elastic region, the true stress (σ) − true strain (ε) variation of a material beyond yielding follows the equation σ =400ε0.3 MPa. The engineering ultimate tensile strength value of this material is ________ MPa. (Rounded off to one decimal place) (2024)
(a) 145.6
(b) 325.6
(c) 206.6
(d) 125.2
Ans: (c)
Sol:

The true strain (εT) at the onset of necking equal to the strain hardening exponent i.e. at ultimate tensile point.
So, 𝜀T=n=0.3 at ultimate point
So, from equation (i)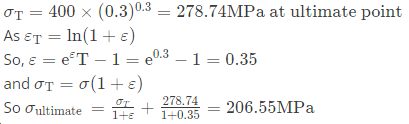
Q3: The principal stresses at a point P in a solid are 70 MPa, -70 MPa and 0. The yield stress of the material is 100 MPa. Which prediction(s) about material failure at P is/are CORRECT? (2024)
(a) Maximum normal stress theory predicts that the material fails
(b) Maximum shear stress theory predicts that the material fails
(c) Maximum normal stress theory predicts that the material does not fail
(d) Maximum shear stress theory predicts that the material does not fail
Ans: (b, c)
Sol: 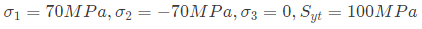
For maximum shear stress theory:
So material will fail As per maximum normal stress theory:
𝜎1 and sigma2 > sigmayt
then material will fail
Here 70 & -70 < 100
So material is safe.
Q4: A prismatic bar PQRST is subjected to axial loads as shown in the figure. The segments having maximum and minimum axial stresses, respectively, are (2024)

(a) QR and PQ
(b) ST and PQ
(c) QR and RS
(d) ST and RS
Ans: (d)
Sol: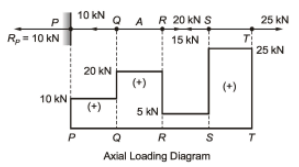
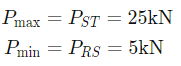
Hence, maximum and minimum axial stresses are in ST and RS portions because of prismatic bar.
Q5: The loading and unloading response of a metal is shown in the figure. The elastic and plastic strains corresponding to 200 MPa stress, respectively, are (2021 Set- 1)
(a) 0.01 and 0.01
(b) 0.02 and 0.01
(c) 0.01 and 0.02
(d) 0.02 and 0.02
Ans: (b)
Sol: Elastic strain : Which can be recovered = 0.03 - 0.01 = 0.02
Plastic strain : Permanent strain = 0.01
Q6: Uniaxial compression test data for a solid metal bar of length 1 m is shown in the figure. (2020 Set- 2)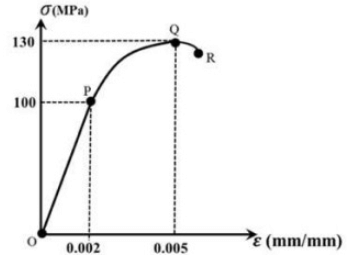
The bar material has a linear elastic response from O to P followed by a non-linear response. The point P represents the yield point of the material. The rod is pinned at both the ends. The minimum diameter of the bar so that it does not buckle under axial loading before reaching the yield point is _______ mm (round off to one decimal place).
(a) 16.56
(b) 56.94
(c) 78.25
(d) 68.42
Ans: (b)
Sol:
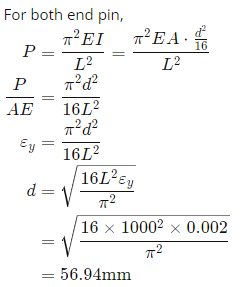
Q7: Bars of square and circular cross-section with 0.5 m length are made of a material with shear strength of 20 MPa. The square bar cross-section dimension is 4 cm x 4 cm and the cylindrical bar cross-section diameter is 4 cm. The specimens are loaded as shown in the figure. (2020 Set- I)

Which specimen(s) will fail due to the applied load as per maximum shear stress theory?
(a) Tensile and compressive load specimens
(b) Torsional load specimen
(c) Bending load specimen
(d) None of the specimens
Ans: (a)
Sol: 
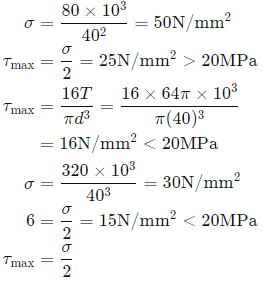
Q8: Consider a linear elastic rectangular thin sheet of metal, subjected to uniform uniaxial tensile stress of 100 MPa along the length direction. Assume plane stress conditions in the plane normal to the thickness. The Young's modulus E=200 MPa and Poisson's ratio v=0.3 are given. The principal strains in the plane of the sheet are (2019 Set -2)
(a) (0.35, -0.15)
(b) (0.5, 0.0)
(c) (0.5, -0.15)
(d) (0.5,-0.5)
Ans: (c)
Sol: 
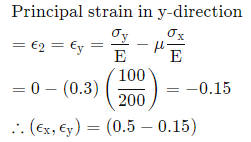
Q9: In a UTM experiment, a sample of length 100 mm, was loaded in tension until failure. The failure load was 40 kN. The displacement, measured using the cross-head motion, at failure, was 15 mm. The compliance of the UTM is constant and is given by 5 x 10-8 m/N. The strain at failure in the sample is _______%. (2019 Set -1)
(a) 8
(b) 16
(c) 13
(d) 6
Ans: (c)
Sol: 
Q10: A plane-strain compression (forging) of a block is shown in the figure. The strain in the z-direction is zero. The yield strength (Sy) in uniaxial tension/compression of the material of the block is 300 MPa and it follows the Tresca (maximum shear stress) criterion. Assume that the entire block has started yielding. At a point where σx = 40M Pa, (compressive) and τxy = 0, the stress component σy is (2019 Set - 1)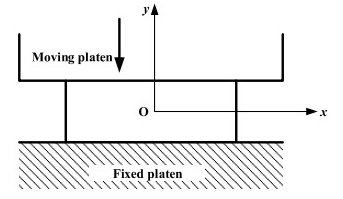
(a) 340 MPa (compressive)
(b) 340 MPa (tensile)
(c) 260 MPa (compressive)
(d) 260 MPa (tensile)
Ans: (a)
Sol: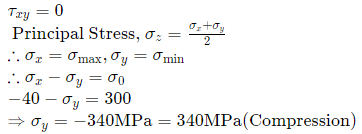
Q11: Consider the stress-strain curve for an ideal elastic-plastic strain hardening metal as shown in the figure. The metal was loaded in uniaxial tension starting from O. Upon loading, the stress-strain curve passes through initial yield point at P, and then strain hardens to point Q, where the loading was stopped. From point Q, the specimen was unloaded to point R, where the stress is zero. If the same specimen is reloaded in tension from point R, the value of stress at which the material yields again is _________ MPa. (2019 Set-1)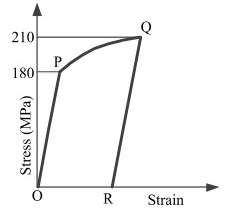 (a) 210
(a) 210
(b) 70
(c) 420
(d) 480
Ans: (a)
Sol: Yield strength will increase to 210 MPa due to strain hardening.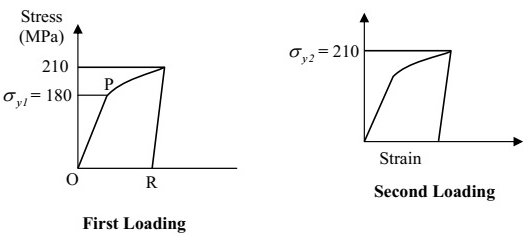
Q12: A solid cube of side 1 m is kept at a room temperature of 32ºC. The coefficient of linear thermal expansion of the cube material is 1 x 10-5/ºC and the bulk modulus is 200 GPa.If the cube is constrained all around and heated uniformly to 42ºC, then the magnitude of volumetric (mean) stress (in MPa) induced due to heating is____ (2019 Set-1)
(a) 20
(b)60
(c) 80
(d) 100
Ans: (b)
Sol: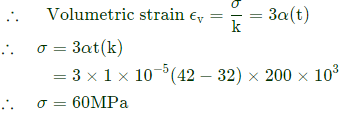
Q13: The State of stress at a point, for a body in place stress, is shown in the figure below. If the minimum principal stress is 10 kPa, then the normal stress σs (in kPa) is (2018)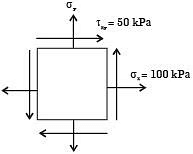 (a) 9.45
(a) 9.45
(b) 18.88
(c) 37.78
(d) 75.50
Ans: (c)
Sol:
σx = 100 k Pa, txy = 50 k Pa
Minimum principal stress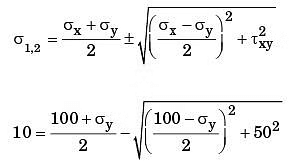
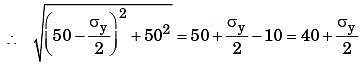 By squaring
By squaring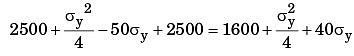
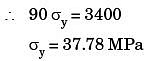
Q14: The state of stress at a point on an element is shown in figure (a). The same state of stress is shown in another coordinate system in figure (b). (2016)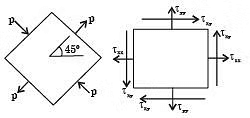 The components (txx, tyy, txy,) are given by
The components (txx, tyy, txy,) are given by
(a) 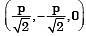
(b) (0, 0, p)
(c)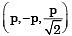
(d) 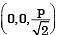
Ans: (b)
Sol: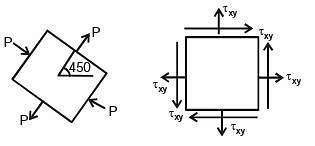
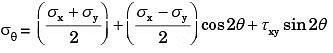 Here θ = - 45
Here θ = - 45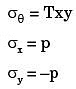
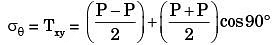 = 0
= 0
When θ = +45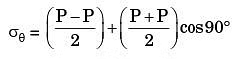
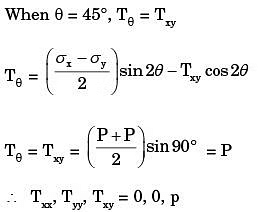
Q15: The principal stresses at a point inside a solid object are σ1 = 100 MPa, σ2 = 100 MPa and σ3 = 0 MPa. The yield strength of the material is 200 MPa. The factor of safety calculated using Tresca (maximum shear stress) theory is nT and the factor of safety calculated using Von Mises(maximum distortional energy) theory is nv. Which one of the following relations is TRUE? (2016)
(a) 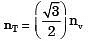
(b) 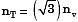
(c) nT = nv
(d) 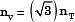
Ans: (c)
Sol:
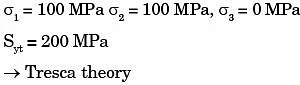

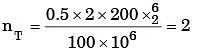 → Von mises theory
→ Von mises theory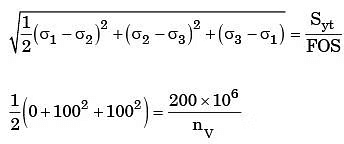
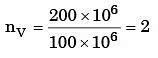 ∴ nT = nv
∴ nT = nv
Q16: The principal stresses at a point in a critical -section of a machine component are σ1 = 60 MPa, σ2 = 5 MPa and σ3 = - 40 MPa. For the material of the component, the tensile yield strength is σy = 200 MPa. According to the maximum shear stress theory, the factor of safety is (2016)
(a) 1.67
(b) 2.00
(c) 3.60
(d) 4.00
Ans: (b)
Sol:
σ1 = 60 MPa, σ2 = 5MPa σ3 = - 40 MPa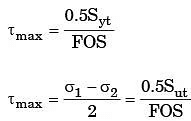
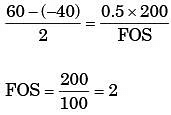
Q17: In a plane stress condition, the components of stress at a point are σx = 20 MPa, σy = 80 MPa and σxy = 40 MPa. The maximum shear stress (in MPa) at the point is
(a) 20
(b) 25
(c) 50
(d) 100
Ans: (c)
Sol: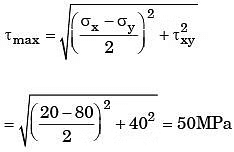
Q18: The homogenous state of stress for a metal part undergoing plastic deformation is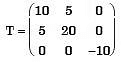 Where the stress component values are in MPa. Using Von Mises yield criterion, the value of estimated shear yield stress, in MPa is (2012)
Where the stress component values are in MPa. Using Von Mises yield criterion, the value of estimated shear yield stress, in MPa is (2012)
(a) 9.50
(b) 16.07
(c) 28.52
(d) 49.41
Ans: (b)
Sol: We know, σ11 = 10, σ22 = 20,
We know, σ11 = 10, σ22 = 20,
σ33 = -10;
σ12 = 5;
σ23 = σ13 = 0
∴ σeq = 27.839 MPa
Shear stress at yield, 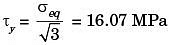
Q19: Match the following criteria of material failure, under biaxial stresses σ1 and σ2 and yield stress σy, with their corresponding graphic representations: (2011)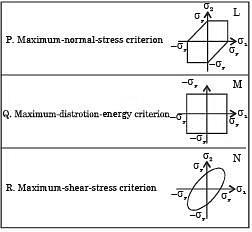
(a) P–M, Q–L, R–N
(b) P–M, Q–N, R–L
(c) P–N, Q–M, R–L
(d) Q–N, Q–L, R–M
Ans: (c)
Q20: The state of plane-stress at a point is given by σx =200 MPa, σy =100 MPa and τxy = 100 MPa. The maximum shear stress
(a) 111.8
(b) 150.1
(c) 180.3
(d) 223.6
Ans: (a)
Sol: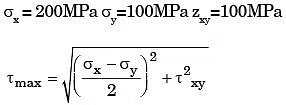
 = 111.80 MPa.
= 111.80 MPa.
Q21: If the principal stresses in a plane stress problem are σ1 = 100 MPa, σ2 = 40 MPa, the magnitude of the maximum shear stress (in MPa) will be (2009)
(a) 60
(b) 50
(c) 30
(d) 20
Ans: (c)
Sol:
Maximum shear stress,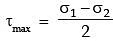

Q22: According to Von-Mises' distortion energy theory, the distortion energy under three dimensional stress state is represented by (2006)
(a) 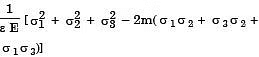
(b) 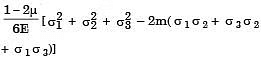
(c) 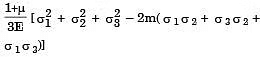
(d) 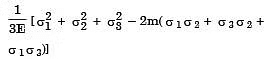
Ans: (c)
Sol: 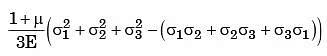
Q23: A shaft subjected to torsion experiences a pure shear stress x on the surface. The maximum principal stress on the surface which is at 45° to the axis will have a value (2003)
(a) τ cos 45°
(b) 2τ cos 45°
(c) τ cos2 45°
(d) 2τ sin 45° cos 45°
Ans: (d)
Sol: 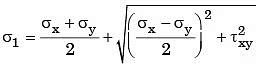
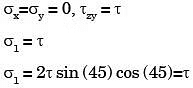
Q24: If the two principal strains at a point are 1000 x 10-6 and –600 × 10–6, then the maximum shear strain is (1996)
(a) 800 x 10-6
(b) 500 x 10-6
(c) 1600 x 10-6
(d) 200 x 10-6
Ans: (c)
Sol: 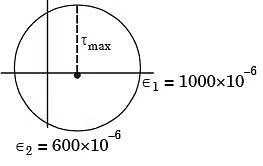
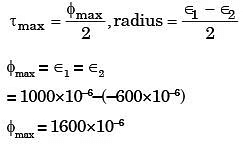
Q25: At a point in a stressed body the state of stress on two planes 45° apart is as shown below. Determine the two principal stresses in MPa.
(a) 8.242, 0.658
(b) 8.242, 0.758
(c) 9.234, 0.757
(d) 9.242, 0.758
Ans: (d)
Sol: 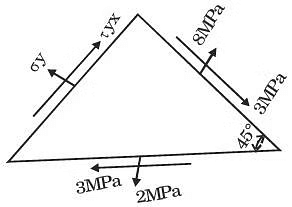
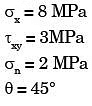
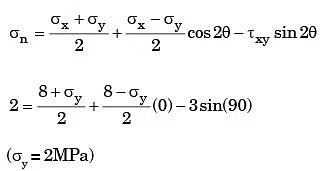
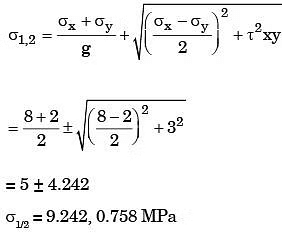
Q26: A large uniform plate containing a rivet hole is subjected to uniform uniaxial tension of 95 MPa. The maximum stress in the plate is (1992)
(a) 100 MPa
(b) 285 MPa
(c) 190 MPa
(d) Indetermine
Ans: (b)
Sol: 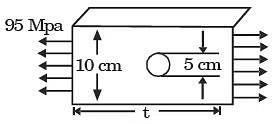
Q27: The three-dimensional state of stress at a point is given by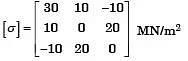 The shear stress on the x-face in y-direction at the same point is then equal to (1990)
The shear stress on the x-face in y-direction at the same point is then equal to (1990)
(a) zero MN/m2
(b) -10 MN/m2
(c) 10 MN/m2
(d) 20 MN/m2
Ans: (c)
Sol: 

Q28: An elastic body is subjected to a tensile stress X in a particular direction and a compressive stress Y in its perpendicular direction. X and Y are unequal in magnitude. On the plane of maximum shear stress in the body there will be (1989)
(a) no normal stress
(b) also the maximum normal stress
(c) the minimum normal stress
(d) both normal stress and shear stress
Ans: (c)
|
37 videos|39 docs|45 tests
|
FAQs on GATE Past Year Questions: Principal Stress & Strain - Strength of Materials (SOM) - Mechanical Engineering
| 1. What is the difference between principal stress and principal strain? |  |
| 2. How do you determine the principal stresses in a material? |  |
| 3. What is the significance of principal stresses in mechanical engineering? |  |
| 4. Can principal stresses be negative? |  |
| 5. How do principal strains affect the deformation behavior of materials? |  |

|
Explore Courses for Mechanical Engineering exam
|

|

















