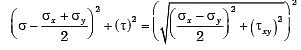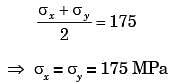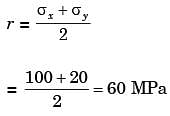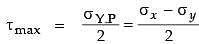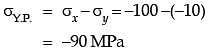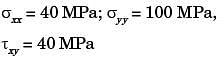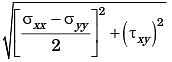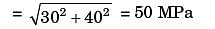GATE Past Year Questions: Mohr's Circle | Strength of Materials (SOM) - Mechanical Engineering PDF Download
Q1: Which of the plot(s) shown is/are valid Mohr's circle representations of a plane stress state in a material? (The center of each circle is indicated by O.) (2023)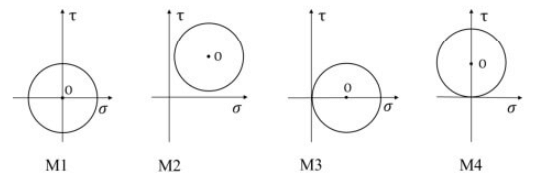
(a) M1
(b) M2
(c) M3
(d) M4
Ans: (a,c)
Sol: Mohr's circle is a graphical representation of plane stress and shear stress.
Mohr's circle is always symmetrical about the x-axis.
Q2: A linear elastic structure under plane stress condition is subjected to two sets of loading, I and II. The resulting states of stress at a point corresponding to these two loadings are as shown in the figure below. If these two sets of loading are applied simultaneously, then the net normal component of stress σxx is ________. (2022 Set - 2)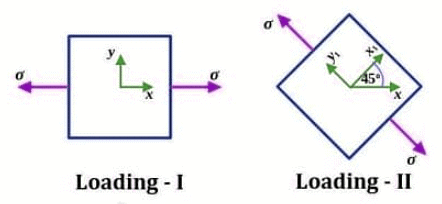
(a) 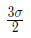
(b) 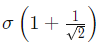
(c) 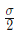
(d) 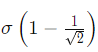
Ans: (a)
Sol: 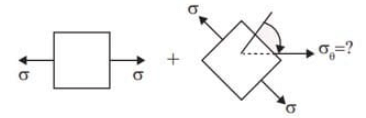

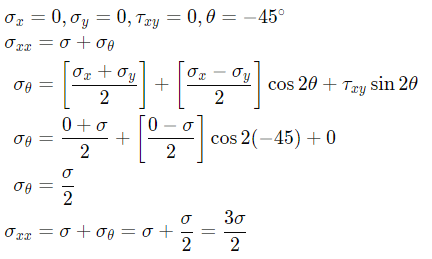
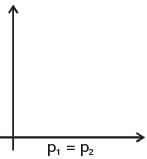
Q3: The stress state at a point in a material under plane stress condition is equi-biaxial tension with a magnitude of 10 MPa. If one unit on the σ−τ plane is 1 MPa, the Mohr's circle representation of the state-of-stress is given by (2020 Set -1)
(a) a circle with a radius equal to principal stress and its center at the origin of the σ−τ plane
(b) a point on the σ axis at a distance of 10 units from the origin
(c) a circle with a radius of 10 units on the σ-τ plane.
(d) a point on the τ axis at a distance of 10 units from the origin
Ans: (b)
Sol: 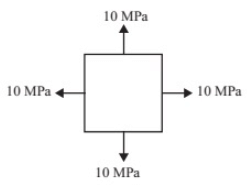

The given state of stress is represented by a point on σ−τ graph which is located on σ-axis at a distance of 10 units from origin.
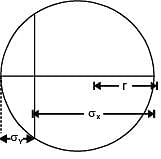
Q4: The state of stress at a point in a component is represented by a Mohr's circle of radius 100MPa centered at 200 MPa on the normal stress axis. On a plane passing through the same point, the normal stress is 260 MPa. The magnitude of the shear stress on the same plane at the same point is ______ MPa. (2019 Set -2)
(a) 48
(b) 63
(c) 96
(d) 80
Ans: (d)
Sol: 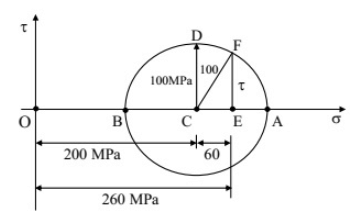

EF→Represents shear stress at the same point =EF=τ=80MPa
Q5: The state of stress at a point, for a body in plane stress, is shown in the figure below. If the minimum principal stress is 10 kPa, then the normal stress σy (in kPa) is (2018 Set - 1)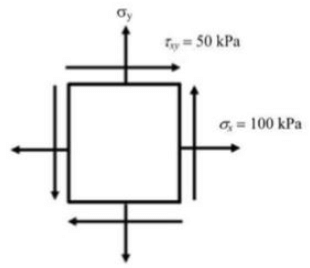
(a) 9.45
(b) 18.88
(c) 37.78
(d) 75.5
Ans: (c)
Sol: 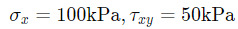
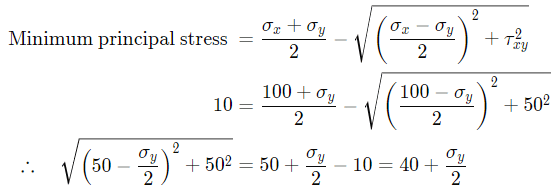
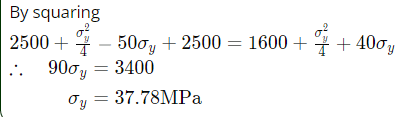
Q6: If σ1 and σ3 are the algebraically largest and smallest principal stresses respectively, the value of the maximum shear stress is
(a) 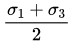
(b) 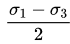
(c) 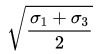
(d) 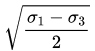
Ans: (b)
Sol:
Maximum shear stress is 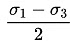
Q7: The state of stress at a point is 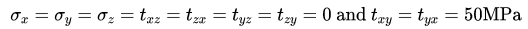
The maximum normal stress (in MPa) at that point is_____. (2017 Set -2)
(a) 49
(b) 50
(c) 55
(d) 60
Ans: (b)
Sol: Given state of stress condition indicates pure shear state of stress.
For pure shear state of stress,
Max. tensile stress = Max. comp. stress = Max. Shear stress = τXY =50MPa
Hence, Max. normal stress =50MPa
Q8: In a plane stress condition, the components of stress at a point are σx = 20 M Pa, σy = 80M Pa and τxy=40MPa . The maximum shear stress (in MPa) at the point is (2015 Set - 2)
(a) 20
(b) 25
(c) 50
(d) 100
Ans: (c)
Sol: 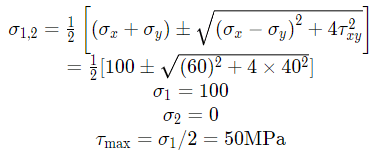
[2003]
The maximum and minimum principal stresses respectively from the Mohr's circle are
[2003]
The directions of maximum and minimum principal stresses at the point P from the Mohr's circle are
[2004]
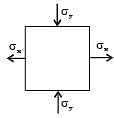
[2005]
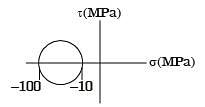
[2008]
[2012]
σxx = 40 MPa, σyy = 100 MPa and σxy =40 MPa
The radius of Mohr's circle representing the given state of stress in MPa is
|
37 videos|39 docs|45 tests
|
FAQs on GATE Past Year Questions: Mohr's Circle - Strength of Materials (SOM) - Mechanical Engineering
| 1. What is Mohr's Circle used for in mechanical engineering? |  |
| 2. How is Mohr's Circle constructed for a given stress state? |  |
| 3. What is the significance of Mohr's Circle in material analysis? |  |
| 4. How can Mohr's Circle be used to determine the principal stresses of a material? |  |
| 5. Can Mohr's Circle be used for strain analysis in addition to stress analysis? |  |

|
Explore Courses for Mechanical Engineering exam
|

|