All Courses
Get the App Signup / Login
Sign in Open App
Mechanical Engineering Exam  >  Mechanical Engineering Notes  >  Strength of Materials (SOM)  >  GATE Past Year Questions: Bending of Beams

GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering PDF Download

Q1: Which of the following beam(s) is/are statically indeterminate?    (2024)
(a) GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering
(b) GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering
(c) GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering
(d) GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering
Ans: (c,d)
Sol: Statically indeterminate structures are those structures that cannot be analyzed using statics or equations of equilibrium. In such cases, the number unknowns exceeds the number of equilibrium equation available. Checking each option: For option (A), Number of unknown=2 Number of equilibrium equation=2 For option (B), Number of unknown=2 Number of equilibrium equation=2 For option (C), Number of unknown=3 Number of equilibrium equation=2 For option (D), Number of unknown=3 Number of equilibrium equation=3 So, (C) is statically indeterminate structures. Note: Official answer key has been given as option (C) and (D), which can be challenged by students.

Statically indeterminate structures are those structures that cannot be analyzed using statics or equations of equilibrium. In such cases, the number unknowns exceeds the number of equilibrium equation available.

Checking each option:

For option (A),
Number of unknown=2
Number of equilibrium equation=2

For option (B),
Number of unknown=2
Number of equilibrium equation=2

For option (C),
Number of unknown=3
Number of equilibrium equation=2

For option (D),
Number of unknown=3
Number of equilibrium equation=3

So, (C) is statically indeterminate structures. Note: Official answer key has been given as option (C) and (D), which can be challenged by students.

Q2: The effective stiffness of a cantilever beam of length L and flexural rigidity EI subjected to a transverse tip load W is     (2023)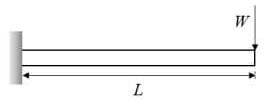
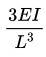
GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering

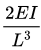
(a) GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering
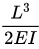
(b) GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering
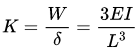
(c) GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering
(d) GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering
Ans: (a)
Sol: GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering

Q3: A cantilever beam with a uniform flexural rigidity 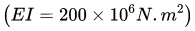GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering is loaded with a concentrated force at its free end. The area of the bending moment diagram corresponding to the full length of the beam is 10000 N.m2. The magnitude of the slope of the beam at its free end is ____________micro radian (round off to the nearest integer).     (2021 Set - 2)
(a) 42
(b) 50
(c) 65
(d) 84
Ans: (b)
Sol: 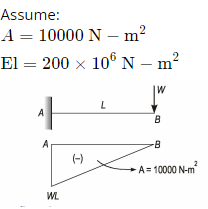GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering
GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering

Q4: A plane frame PQR (fixed at P and free at R) is shown in the figure. Both members (PQ and QR) have length, L, and flexural rigidity, EI. Neglecting the effect of axial stress and transverse shear, the horizontal deflection at free end, R, is     (2021 Set - 2)

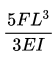
GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering

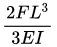
(a) GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering
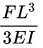
(b) GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering
(c) GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering
(d) GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering
Ans: (b)
Sol: 
GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering

GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering

Q5: An overhanging beam PQR is subjected to uniformly distributed load 20 kN/m as shown in the figure.     (2021 Set - 1)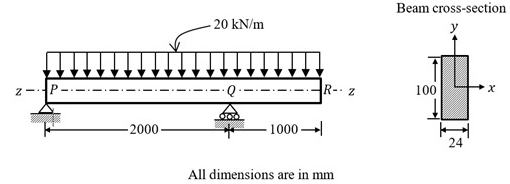
GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering

The maximum bending stress developed in the beam is ________MPa (round off to one decimal place).
(a) 125
(b) 250
(c) 325
(d) 450
Ans: (b)
Sol: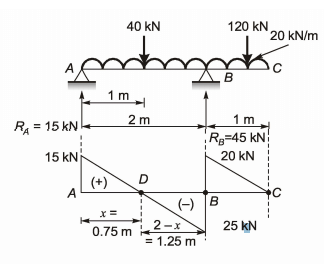 
GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering

GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering

GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering

GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering

GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering

Q6: A cantilever beam of length, L, and flexural rigidity, EI, is subjected to an end moment, M, as shown in the figure. The deflection of the beam at x = L/2 is     (2021 Set -1)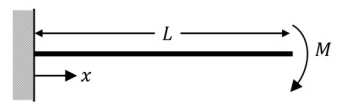
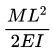
GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering
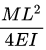
(a) GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering
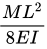
(b) GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering
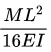
(c) GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering
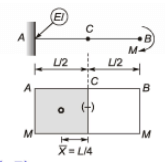
(d) GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering
Ans: (c)
Sol:  GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering
GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering

Q7: A cantilever of length l, and flexural rigidity EI, stiffened by a spring of stiffness k, is loaded by transverse force P, as shown

GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering
The transverse deflection under the load is      (2020 Set - 2)
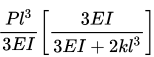
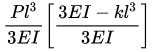
(a) GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering
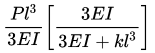
(b) GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering
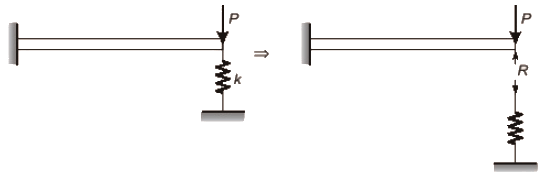
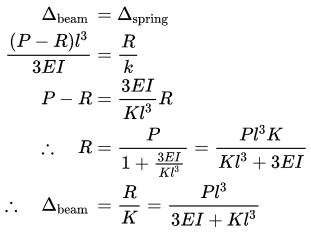
(c) GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering
(d) GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering
Ans: (d)
Sol: 
GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering
GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering

Q8:  A horizontal cantilever beam of circular cross-section, length 1.0 m and flexural rigidity EI= 200 N.m2 is subjected to an applied moment MA= 1.0 N⋅m at the free end as shown in the figure. The magnitude of the vertical deflection of the free end is _______mm (round off to one decimal place).    (2019 Set -2)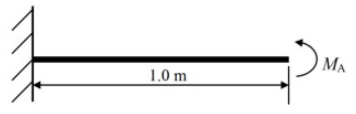
GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering
(a) 1.2
(b) 5.3
(c) 8.2
(d) 2.5
Ans: (d)
Sol: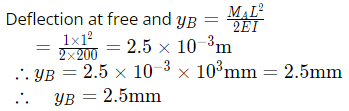
GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering

Q9: A prismatic, straight, elastic, cantilever beam is subjected to a linearly distributed transverse load as shown below. If the beam length is L, Young's modulus E, and area moment of inertia I, the magnitude of the maximum deflection is     (2019 Set -2)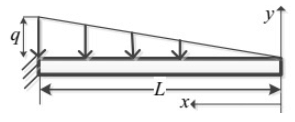
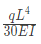
GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering

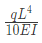
(a) GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering
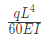
(b) GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering
(c) GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering
(d) GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering
Ans: (b)
Sol: Double Integration method:
Let x be distance from the free end

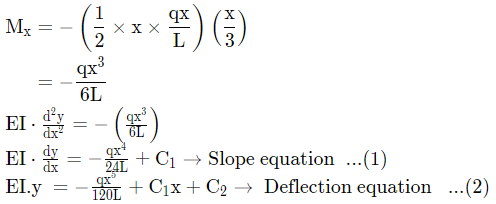
GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering
GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering

Q10: Consider a prismatic straight beam of length L=πm, pinned at the two ends as shown in the figure. The beam has a square cross-section of side p=6 mm. The Young's modulus E= 200 GPa, and the coefficient of thermal expansion α=3×10-6K-1. The minimum temperature rise required to cause Euler buckling of the beam is ________ K.    (2019 Set - 1)
GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering(a) 0
(b) 0.5
(c) 1
(d) 2
Ans: (c)
Sol: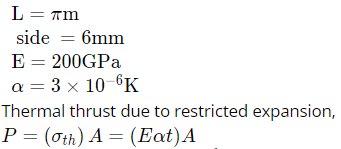
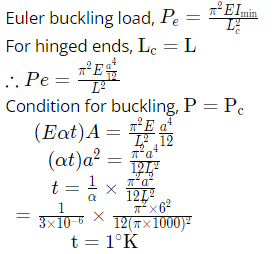
GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering
GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering

Q11: Consider an elastic straight beam of length L=10πm, with square cross-section of side a=5 mm, and Young's modulus E=200 GPa. This straight beam was bent in such a way that the two ends meet, to form a circle of mean radius R. Assuming that Euler-Bernoulli beam theory is applicable to this bending problem, the maximum tensile bending stress in the bent beam is __________ MPa.    (2019 Set-1)
GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering
(a) 100
(b) 200
(c) 50
(d)150
Ans: (a)
Sol: 
L = 10π m
a = 5 mm
E = 200 GPa
Length of wire: L = πD = 2πR
10π = 2πR
R = 5 m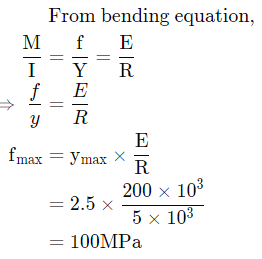
GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering

Q12: The minimum axial compressive load, P, required to initiate buckling for a pinned-pinned slender column with bending stiffness EI and length L is    (2018 Set -2)
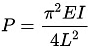
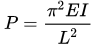
(a) GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering
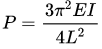
(b) GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering
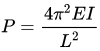
(c) GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering
(d) GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering
Ans: (b)
Sol:
For both ends hinged buckling load,
GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering

Q13: A steel column of rectangular section (15 mm x 10 mm) and length 1.5 m is simply supported at both ends. Assuming modulus of elasticity, E = 200 GPa for steel, the critical axial load (in kN) is ____ (correct to two decimal places). 
(a) 2.25
(b) 1.09
(c) 2.04
(d) 2.68
Ans: (b)
Sol:
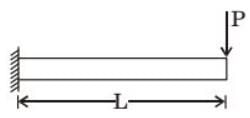
GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering

Question for GATE Past Year Questions: Bending of Beams
Try yourself:A tapered cantilever beam of constant thickness is loaded as shown in the sketch below. The bending stress will be
GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering
GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering

[1988]

View Solution

Question for GATE Past Year Questions: Bending of Beams
Try yourself:Which one of the following diagrams shows correctly the distribution of transverse shear stress across the depth h of a rectangular beam subjected to varying bending moment along its length?
View Solution

Question for GATE Past Year Questions: Bending of Beams
Try yourself:The second moment of a circular area about the diameter is given by (D is the diameter)
View Solution

Question for GATE Past Year Questions: Bending of Beams
Try yourself:The beams, one having square cross-section and another circular cross-section, are subjected to the same amount of bending moment. If the cross sectional area as well as the material of both the beams are the same then

[2003]

View Solution

Question for GATE Past Year Questions: Bending of Beams
Try yourself:A cantilever beam has the square cross section of 10 mm × 10 mm. It carries a transverse load of 10 N. Considering only the bottom fibres of the beam, the correct representation of the longitudinal variation of the bending stress is
GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering

[2005]

View Solution

Question for GATE Past Year Questions: Bending of Beams
Try yourself:A machine frame shown in the figure below is subjected to a horizontal force of 600 N parallel to z-direction.​
GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering
The normal and shear stresses in MPa at point P are respectively

[2007]

View Solution

Question for GATE Past Year Questions: Bending of Beams
Try yourself:The maximum principal stress in MPa and the orientation of the corresponding principal plane in degrees are respectively.

[2007]

View Solution

Question for GATE Past Year Questions: Bending of Beams
Try yourself:A massless beam has a loading pattern as shown in the figure. The beam is of rectangular crosssection with a width of 30 mm and height of 100 mm.​The maximum bending moment occurs at
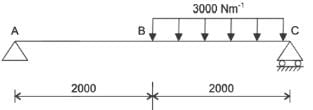
GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering

[2010]

View Solution

Question for GATE Past Year Questions: Bending of Beams
Try yourself:A massless beam has a loading pattern as shown in the figure. The beam is of rectangular cross-section with a width of 30mm and height of 100mm.
GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering

The maximum magnitude of bending stress (in MPa) is given by [2010]
View Solution

Question for GATE Past Year Questions: Bending of Beams
Try yourself:A triangular-shaped cantilever beam of uniformthickness is shown in the figure. The Young's modulus of the material of the beam is E. A concentrated load P is applied at the free end of the beam.
GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering
The area moment of inertia about the neutral axis of a cross-section at a distance x measured from the free end is

[2011]

View Solution

Question for GATE Past Year Questions: Bending of Beams
Try yourself:The maximum deflection of the beam is

[2011]

View Solution

Question for GATE Past Year Questions: Bending of Beams
Try yourself:Consider a simply supported beam of length, 50h, wM             

[2014]

View Solution

Question for GATE Past Year Questions: Bending of Beams
Try yourself: The value of moment of inertia of the section shown in the figure about the axis-XX is
GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering

[2015]

View Solution

Question for GATE Past Year Questions: Bending of Beams
Try yourself:A beam of length L is carrying a uniformly distributed load w per unit length. The flexural rigidity of the beam is EI. The reaction at the simple support at the right end is
GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering

[2016]

View Solution

Question for GATE Past Year Questions: Bending of Beams
Try yourself:Consider a beam with circular cross-section of diameter d. The ratio of the second moment of area about the neutral axis to the section modulus of the area is

[2017]

View Solution

Question for GATE Past Year Questions: Bending of Beams
Try yourself:The transverse shear stress acting in a beam of rectangular cross-section, subjected to a transverse shear load, is

[2008]

View Solution

Question for GATE Past Year Questions: Bending of Beams
Try yourself:An axial residual compressive stress due to a manufacturing process is present on the outer surface of a rotating shaft subjected to bending.Under a given bending load, the fatigue life of the shaft in the presence of the residual compressive stress is

[2008]

View Solution

Question for GATE Past Year Questions: Bending of Beams
Try yourself:A solid circular shaft of diameter 100 mm is subjected to an axial stress of 50 MPa. It is further subjected to a torque of 10 kNm. The maximum principal stress experienced on the shaft is closest to

[2008]

View Solution

The document GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering is a part of the Mechanical Engineering Course Strength of Materials (SOM).
All you need of Mechanical Engineering at this link: Mechanical Engineering
37 videos|39 docs|45 tests
Join Course for Free

Top Courses for Mechanical Engineering

FAQs on GATE Past Year Questions: Bending of Beams - Strength of Materials (SOM) - Mechanical Engineering

1. What is the formula for calculating the bending stress in a beam?
Ans. The formula for calculating bending stress in a beam is given by σ = M*c/I, where σ is the bending stress, M is the bending moment, c is the distance from the neutral axis to the outermost fiber, and I is the moment of inertia.
2. How do you determine the maximum deflection of a beam under a certain load?
Ans. The maximum deflection of a beam under a certain load can be determined using the formula δ = (5*P*L^3)/(384*E*I), where δ is the maximum deflection, P is the applied load, L is the length of the beam, E is the modulus of elasticity, and I is the moment of inertia.
3. What are the different types of beams based on their support conditions?
Ans. Beams can be classified into different types based on their support conditions, such as simply supported beams, cantilever beams, fixed beams, and continuous beams.
4. How does the material properties of a beam affect its bending behavior?
Ans. The material properties of a beam, such as modulus of elasticity and yield strength, play a significant role in determining its bending behavior. Beams with higher modulus of elasticity and yield strength will exhibit less deflection and higher resistance to bending stresses.
5. What is the significance of the neutral axis in the bending of beams?
Ans. The neutral axis is an imaginary line within a beam where there is no change in length during bending. It is a critical component in calculating bending stresses and deflections in beams.
Related Exams
About this Document
4.89/5 Rating
Oct 29, 2024 Last updated
Document Description: GATE Past Year Questions: Bending of Beams for Mechanical Engineering 2024 is part of Strength of Materials (SOM) preparation. The notes and questions for GATE Past Year Questions: Bending of Beams have been prepared according to the Mechanical Engineering exam syllabus. Information about GATE Past Year Questions: Bending of Beams covers topics like and GATE Past Year Questions: Bending of Beams Example, for Mechanical Engineering 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for GATE Past Year Questions: Bending of Beams.
Introduction of GATE Past Year Questions: Bending of Beams in English is available as part of our Strength of Materials (SOM) for Mechanical Engineering & GATE Past Year Questions: Bending of Beams in Hindi for Strength of Materials (SOM) course. Download more important topics related with notes, lectures and mock test series for Mechanical Engineering Exam by signing up for free. Mechanical Engineering: GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering
Description
Full syllabus notes, lecture & questions for GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering - Mechanical Engineering | Plus excerises question with solution to help you revise complete syllabus for Strength of Materials (SOM) | Best notes, free PDF download
Information about GATE Past Year Questions: Bending of Beams
In this doc you can find the meaning of GATE Past Year Questions: Bending of Beams defined & explained in the simplest way possible. Besides explaining types of GATE Past Year Questions: Bending of Beams theory, EduRev gives you an ample number of questions to practice GATE Past Year Questions: Bending of Beams tests, examples and also practice Mechanical Engineering tests
37 videos|39 docs|45 tests
Join Course for Free
Download as PDF
Explore Courses for Mechanical Engineering exam

Top Courses for Mechanical Engineering

Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
10M+ students study on EduRev
Related Searches

Extra Questions

,

Semester Notes

,

Important questions

,

practice quizzes

,

MCQs

,

video lectures

,

past year papers

,

pdf

,

Objective type Questions

,

Previous Year Questions with Solutions

,

Summary

,

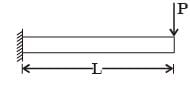
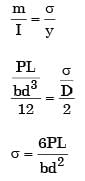
GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering

,

study material

,

shortcuts and tricks

,

GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering

,

Sample Paper

,

Free

,

ppt

,

Exam

,

mock tests for examination

,

GATE Past Year Questions: Bending of Beams | Strength of Materials (SOM) - Mechanical Engineering

,

Viva Questions

;
Additional Information about GATE Past Year Questions: Bending of Beams for Mechanical Engineering Preparation

GATE Past Year Questions: Bending of Beams Free PDF Download

The GATE Past Year Questions: Bending of Beams is an invaluable resource that delves deep into the core of the Mechanical Engineering exam. These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective. With the help of these notes, you can grasp complex subjects quickly, revise important points easily, and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner, allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material, or toppers' notes, this PDF has got you covered. Download the GATE Past Year Questions: Bending of Beams now and kickstart your journey towards success in the Mechanical Engineering exam.

Importance of GATE Past Year Questions: Bending of Beams

The importance of GATE Past Year Questions: Bending of Beams cannot be overstated, especially for Mechanical Engineering aspirants. This document holds the key to success in the Mechanical Engineering exam. It offers a detailed understanding of the concept, providing invaluable insights into the topic. By knowing the concepts well in advance, students can plan their preparation effectively. Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.

GATE Past Year Questions: Bending of Beams Notes

GATE Past Year Questions: Bending of Beams Notes offer in-depth insights into the specific topic to help you master it with ease. This comprehensive document covers all aspects related to GATE Past Year Questions: Bending of Beams. It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation. Practice papers and question papers enable you to assess your progress effectively. Additionally, the paper analysis provides valuable tips for tackling the exam strategically. Access to Toppers' notes gives you an edge in understanding complex concepts. Whether you're a beginner or aiming for advanced proficiency, GATE Past Year Questions: Bending of Beams Notes on EduRev are your ultimate resource for success.

GATE Past Year Questions: Bending of Beams Mechanical Engineering

The "GATE Past Year Questions: Bending of Beams Mechanical Engineering Questions" guide is a valuable resource for all aspiring students preparing for the Mechanical Engineering exam. It focuses on providing a wide range of practice questions to help students gauge their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation. The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level. Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.

Study GATE Past Year Questions: Bending of Beams on the App

Students of Mechanical Engineering can study GATE Past Year Questions: Bending of Beams alongwith tests & analysis from the EduRev app, which will help them while preparing for their exam. Apart from the GATE Past Year Questions: Bending of Beams, students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc. The EduRev App will make your learning easier as you can access it from anywhere you want. The content of GATE Past Year Questions: Bending of Beams is prepared as per the latest Mechanical Engineering syllabus.
© EduRev
Education Revolution
Follow Us
Signup to see your scores go up
within 7 days!
Takes less than 10 seconds to signup