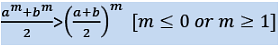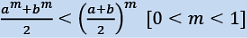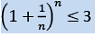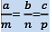CAT Exam > CAT Notes > Quantitative Aptitude (Quant) > Important Formulae: Inequalities
Important Formulas for CAT Inequalities
If a > b and c > 0,
⇒ a + c > b + c
⇒ a - c > b - c
⇒ ac > bc
⇒ a/c > b/c
If a, b ≥ 0, then an > bn and 1/an < 1/bn, where n is positive.
a < b and x > 0, then 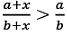
a > b and x > 0, then 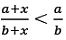
Modular Inequalities
|x- y| = |y - x|
|x. y| = |x| . |y|
|x+ y| < |x| + |y|
|x+ y| > |x| - |y|
Quadratic Inequalities
(x – a) (x – b) > 0 {a < b}
⇒ (x < a) U (x > b)
(x – a) (x – b) < 0 {a > b}
⇒ a < x < b
For any set of positive numbers: AM≥GM≥HM
⇒ (a1+a2+ ….+an)/n ≥(a1.a2. …..an)1/n
If a and b are positive quantities, then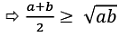
If a,b,c,d are positive quantities, then
⇒ 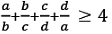
⇒ a4 + b4 + c4 + d4 ≥ 4abcd
If a,b,c …. k are n positive quantities and m is a natural number, then
EduRev's Tip:


- For any positive integer n, 2 ≤

- ambncp……..will be greatest when

- If a > b and both are natural numbers, then
⇒ ab < ba {Except 32 > 23 & 42 = 24} - (n!)2 ≥ nn
- If the sum of two or more positive quantities is constant, their product is greatest when they are equal and if their product is constant then their sum is the least when the numbers are equal.
⇒ If x + y = k, then xy is greatest when x = y
⇒ If xy = k, then x + y is least when x = y
The document Important Formulas for CAT Inequalities is a part of the CAT Course Quantitative Aptitude (Quant).
All you need of CAT at this link: CAT
|
191 videos|131 docs|110 tests
|
FAQs on Important Formulas for CAT Inequalities
| 1. What are some important properties of inequalities? |  |
Ans. Some important properties of inequalities are:
- Multiplying or dividing both sides of an inequality by a positive number does not change the inequality.
- Multiplying or dividing both sides of an inequality by a negative number reverses the inequality.
- Adding or subtracting the same number to both sides of an inequality does not change the inequality.
- If two inequalities are combined with "and," both inequalities must be true for the combined inequality to be true.
- If two inequalities are combined with "or," at least one of the inequalities must be true for the combined inequality to be true.
| 2. How do you solve an inequality with absolute values? |  |
Ans. To solve an inequality with absolute values, you can follow these steps:
1. Set up two separate inequalities, one with the positive value of the absolute value and one with the negative value.
2. Solve each inequality separately to find the range of values that satisfy them.
3. Combine the solutions of both inequalities to determine the final solution.
| 3. What is the difference between a strict inequality and a non-strict inequality? |  |
Ans. In mathematics, a strict inequality is denoted by "<" or ">" and indicates that the two compared values are not equal. For example, "x < 5" means that x is less than 5, but not equal to 5. On the other hand, a non-strict inequality is denoted by "≤" or "≥" and includes the possibility of equality. For example, "x ≤ 5" means that x can be equal to 5 as well.
| 4. How can you represent an inequality graphically? |  |
Ans. An inequality can be represented graphically on a number line or a coordinate plane. For a simple linear inequality, you can plot the inequality as a shaded region on a number line. If the inequality involves two variables, it can be graphed as a shaded region in the coordinate plane. The boundary line separates the region of solutions from the region that does not satisfy the inequality.
| 5. What are some common mistakes to avoid when solving inequalities? |  |
Ans. Some common mistakes to avoid when solving inequalities include:
- Forgetting to reverse the inequality sign when multiplying or dividing by a negative number.
- Incorrectly applying the distributive property while simplifying expressions.
- Not considering the possibility of the variable being equal to a certain value when solving non-strict inequalities.
- Misinterpreting the direction of the inequality symbol when combining or manipulating inequalities.
- Using the wrong inequality symbol (e.g., using "<" instead of "≤") when the inequality includes the possibility of equality.

|
Explore Courses for CAT exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
Related Searches