Practice Doc: CAT 2020 For LRDI (Slot - 3) | Additional Study Material for CAT PDF Download
Instruction
The Hi-Lo game is a four-player game played in six rounds. In every round, each player chooses to bid Hi or Lo. The bids are made simultaneously. If all four bid Hi, then all four lose 1 point each. If three players bid Hi and one bids Lo, then the players bidding Hi gain 1 point each and the player bidding Lo loses 3 points. If two players bid Hi and two bid Lo, then the players bidding Hi gain 2 points each and the players bidding Lo lose 2 points each. If one player bids Hi and three bid Lo, then the player bidding Hi gains 3 points and the players bidding Lo lose 1 point each. If all four bid Lo, then all four gain 1 point each.
Four players Arun, Bankim, Charu, and Dipak played the Hi-Lo game. The following facts are known about their game:
1. At the end of three rounds, Arun had scored 6 points, Dipak had scored 2 points, Bankim and Charu had scored -2 points each.
2. At the end of six rounds, Arun had scored 7 points, Bankim and Dipak had scored -1 point each, and Charu had scored -5 points.
3. Dipak’s score in the third round was less than his score in the first round but was more than his score in the second round.
4. In exactly two out of the six rounds, Arun was the only player who bid Hi.
Q.1. What were the bids by Arun, Bankim, Charu and Dipak, respectively in the first round?
(a) Hi, Lo, Lo, Lo
(b) Lo, Lo, Lo, Hi
(c) Hi, Hi, Lo, Lo
(d) Hi, Lo, Lo, Hi
Ans: d
Solution: From the given information, we can see that the points scored by the players in a round has the following possibilities:
HHHH: (-1, -1, -1, -1)
HHHL: (1, 1, 1, -3)
HHLL: (2, 2, -2, -2)
HLLL: (3, -1, -1, -1)
LLLL: (1, 1, 1, 1)
Also, the total points scored by the four players in a round can only be -4 or 0 or 4.
From (1), the total points scored by the four players combined in the first three rounds is 6 + 2 - 2 - 2 = 4.
Hence, in the first three rounds, the total points scored by the four players must be either (-4, 4, 4) OR (0, 0, 4), in any order.
Also, from (1), in the first three rounds, Arun scored 6 points. And from (2), Arun scored 7 points at the end of round 6. Hence, in the 4th , 5th and 6th rounds, he must have scored 1 point.
From (4), Arun scored 3 points in exactly 2 rounds.
These two rounds cannot both be among 4th , 5th and 6th rounds because he scored a net of only 1 point in these three rounds combined.
Hence, Arun must have scored 3 points in one round among 1st , 2nd and 3 rd rounds. If Arun scored 3 points in the first three rounds, then in that round, the total points scored by the four players combined must be 0 (in the case of HLLL).
Hence, the total points scored by the four players in the first three rounds must be (0, 0, 4). Among the first three rounds, in one round, the three players must have scored (3, -1, -1, -1), with Arun scoring 3 points.
Since in another round, the four players scored a total of 4 points, they must have bid LLLL (as it is the only case in which they can score 4 points in total). They must have scored (1, 1, 1, 1).
In the round that the players scored (3, - 1, - 1, - 1), Dipak must have scored - 1 points (since Arun scored 3 points).
In the round that the players scored (1, 1, 1, 1), Dipak must have scored 1 point.
In the round that the players scored (2, 2, - 2, - 2), Dipak must have scored 2 points (since the total points that Dipak scored in the first three rounds is 2).
From (3), Dipak must have scored 2 points in the first round, - 1 points in the second round and 1 point in the third round.
From this, we can fill the points for the first three rounds, as shown below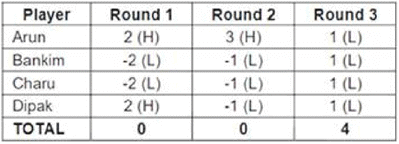
(Note that with this information, the first question of the set can be answered)
In the next three rounds, from (1) and (2), Arun must have scored 1 point, Bankim must have scored 1 point, Charu must have scored - 3 points and Dipak must have scored - 3 points.
The total points scored by the four players are - 4. This is possible if the total points scored by the four players in the three rounds are (0, 0, - 4) OR (4, - 4, - 4) in any order.
However, we know that Arun must have scored 3 points in one of these three rounds (from (4)). Hence, the total points scored by the players in this round must be 0.
Hence, the four players must have scored (0, 0, - 4) points in these three rounds. In one round the points scored by the players must be (3, - 1, - 1, - 1), with Arun scoring 3 points.
In the round in which the total points scored by the four players is 4, they must have scored ( - 1, - 1, - 1, - 1)
Since Bankim scored a total of 1 point in these three rounds, and he scored - 1 point and - 1 point in the two rounds mentioned above, he must have scored 3 points in the other third.
Hence, in the remaining round, the four players must have scored (3, - 1, - 1, - 1), with Bankim scoring 3 points.
However, with the given information, we cannot deduce the round number corresponding to the above rounds.
Hence, we get the following table: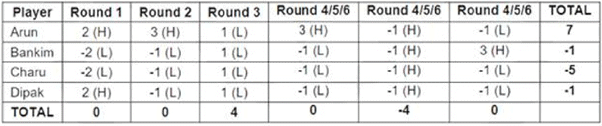
The bids by Arun, Bankim, Charu, Dipak in the first round were Hi, Lo, Lo, Hi.
Q.2. In how many rounds did Arun bid Hi?
Ans: 4
Solution: From the given information, we can see that the points scored by the players in a round has the following possibilities:
HHHH: (-1, -1, -1, -1)
HHHL: (1, 1, 1, -3)
HHLL: (2, 2, -2, -2)
HLLL: (3, -1, -1, -1)
LLLL: (1, 1, 1, 1)
Also, the total points scored by the four players in a round can only be -4 or 0 or 4.
From (1), the total points scored by the four players combined in the first three rounds is 6 + 2 - 2 - 2 = 4.
Hence, in the first three rounds, the total points scored by the four players must be either (-4, 4, 4) OR (0, 0, 4), in any order.
Also, from (1), in the first three rounds, Arun scored 6 points. And from (2), Arun scored 7 points at the end of round 6. Hence, in the 4th , 5th and 6th rounds, he must have scored 1 point.
From (4), Arun scored 3 points in exactly 2 rounds.
These two rounds cannot both be among 4th , 5th and 6th rounds because he scored a net of only 1 point in these three rounds combined.
Hence, Arun must have scored 3 points in one round among 1st , 2nd and 3 rd rounds. If Arun scored 3 points in the first three rounds, then in that round, the total points scored by the four players combined must be 0 (in the case of HLLL).
Hence, the total points scored by the four players in the first three rounds must be (0, 0, 4). Among the first three rounds, in one round, the three players must have scored (3, -1, -1, -1), with Arun scoring 3 points.
Since in another round, the four players scored a total of 4 points, they must have bid LLLL (as it is the only case in which they can score 4 points in total). They must have scored (1, 1, 1, 1).
In the round that the players scored (3, - 1, - 1, - 1), Dipak must have scored - 1 points (since Arun scored 3 points).
In the round that the players scored (1, 1, 1, 1), Dipak must have scored 1 point.
In the round that the players scored (2, 2, - 2, - 2), Dipak must have scored 2 points (since the total points that Dipak scored in the first three rounds is 2).
From (3), Dipak must have scored 2 points in the first round, - 1 points in the second round and 1 point in the third round.
From this, we can fill the points for the first three rounds, as shown below
(Note that with this information, the first question of the set can be answered)
In the next three rounds, from (1) and (2), Arun must have scored 1 point, Bankim must have scored 1 point, Charu must have scored - 3 points and Dipak must have scored - 3 points.
The total points scored by the four players are - 4. This is possible if the total points scored by the four players in the three rounds are (0, 0, - 4) OR (4, - 4, - 4) in any order.
However, we know that Arun must have scored 3 points in one of these three rounds (from (4)). Hence, the total points scored by the players in this round must be 0.
Hence, the four players must have scored (0, 0, - 4) points in these three rounds. In one round the points scored by the players must be (3, - 1, - 1, - 1), with Arun scoring 3 points.
In the round in which the total points scored by the four players is 4, they must have scored ( - 1, - 1, - 1, - 1)
Since Bankim scored a total of 1 point in these three rounds, and he scored - 1 point and - 1 point in the two rounds mentioned above, he must have scored 3 points in the other third.
Hence, in the remaining round, the four players must have scored (3, - 1, - 1, - 1), with Bankim scoring 3 points.
However, with the given information, we cannot deduce the round number corresponding to the above rounds.
Hence, we get the following table:
Arun bid Hi in 4 rounds
Q.3. In how many rounds did Bankim bid Lo?
Ans: 4
Solution: From the given information, we can see that the points scored by the players in a round has the following possibilities:
HHHH: (-1, -1, -1, -1)
HHHL: (1, 1, 1, -3)
HHLL: (2, 2, -2, -2)
HLLL: (3, -1, -1, -1)
LLLL: (1, 1, 1, 1)
Also, the total points scored by the four players in a round can only be -4 or 0 or 4.
From (1), the total points scored by the four players combined in the first three rounds is 6 + 2 - 2 - 2 = 4.
Hence, in the first three rounds, the total points scored by the four players must be either (-4, 4, 4) OR (0, 0, 4), in any order.
Also, from (1), in the first three rounds, Arun scored 6 points. And from (2), Arun scored 7 points at the end of round 6. Hence, in the 4th , 5th and 6th rounds, he must have scored 1 point.
From (4), Arun scored 3 points in exactly 2 rounds.
These two rounds cannot both be among 4th , 5th and 6th rounds because he scored a net of only 1 point in these three rounds combined.
Hence, Arun must have scored 3 points in one round among 1st , 2nd and 3 rd rounds. If Arun scored 3 points in the first three rounds, then in that round, the total points scored by the four players combined must be 0 (in the case of HLLL).
Hence, the total points scored by the four players in the first three rounds must be (0, 0, 4). Among the first three rounds, in one round, the three players must have scored (3, -1, -1, -1), with Arun scoring 3 points.
Since in another round, the four players scored a total of 4 points, they must have bid LLLL (as it is the only case in which they can score 4 points in total). They must have scored (1, 1, 1, 1).
In the round that the players scored (3, - 1, - 1, - 1), Dipak must have scored - 1 points (since Arun scored 3 points).
In the round that the players scored (1, 1, 1, 1), Dipak must have scored 1 point.
In the round that the players scored (2, 2, - 2, - 2), Dipak must have scored 2 points (since the total points that Dipak scored in the first three rounds is 2).
From (3), Dipak must have scored 2 points in the first round, - 1 points in the second round and 1 point in the third round.
From this, we can fill the points for the first three rounds, as shown below
(Note that with this information, the first question of the set can be answered)
In the next three rounds, from (1) and (2), Arun must have scored 1 point, Bankim must have scored 1 point, Charu must have scored - 3 points and Dipak must have scored - 3 points.
The total points scored by the four players are - 4. This is possible if the total points scored by the four players in the three rounds are (0, 0, - 4) OR (4, - 4, - 4) in any order.
However, we know that Arun must have scored 3 points in one of these three rounds (from (4)). Hence, the total points scored by the players in this round must be 0.
Hence, the four players must have scored (0, 0, - 4) points in these three rounds. In one round the points scored by the players must be (3, - 1, - 1, - 1), with Arun scoring 3 points.
In the round in which the total points scored by the four players is 4, they must have scored ( - 1, - 1, - 1, - 1)
Since Bankim scored a total of 1 point in these three rounds, and he scored - 1 point and - 1 point in the two rounds mentioned above, he must have scored 3 points in the other third.
Hence, in the remaining round, the four players must have scored (3, - 1, - 1, - 1), with Bankim scoring 3 points.
However, with the given information, we cannot deduce the round number corresponding to the above rounds.
Hence, we get the following table:
Bankim bid Lo in 4 rounds
Q.4. In how many rounds did all four players make identical bids?
Ans: 2
Solution: From the given information, we can see that the points scored by the players in a round has the following possibilities:
HHHH: (-1, -1, -1, -1)
HHHL: (1, 1, 1, -3)
HHLL: (2, 2, -2, -2)
HLLL: (3, -1, -1, -1)
LLLL: (1, 1, 1, 1)
Also, the total points scored by the four players in a round can only be -4 or 0 or 4.
From (1), the total points scored by the four players combined in the first three rounds is 6 + 2 - 2 - 2 = 4.
Hence, in the first three rounds, the total points scored by the four players must be either (-4, 4, 4) OR (0, 0, 4), in any order.
Also, from (1), in the first three rounds, Arun scored 6 points. And from (2), Arun scored 7 points at the end of round 6. Hence, in the 4th , 5th and 6th rounds, he must have scored 1 point.
From (4), Arun scored 3 points in exactly 2 rounds.
These two rounds cannot both be among 4th , 5th and 6th rounds because he scored a net of only 1 point in these three rounds combined.
Hence, Arun must have scored 3 points in one round among 1st , 2nd and 3 rd rounds. If Arun scored 3 points in the first three rounds, then in that round, the total points scored by the four players combined must be 0 (in the case of HLLL).
Hence, the total points scored by the four players in the first three rounds must be (0, 0, 4). Among the first three rounds, in one round, the three players must have scored (3, -1, -1, -1), with Arun scoring 3 points.
Since in another round, the four players scored a total of 4 points, they must have bid LLLL (as it is the only case in which they can score 4 points in total). They must have scored (1, 1, 1, 1).
In the round that the players scored (3, - 1, - 1, - 1), Dipak must have scored - 1 points (since Arun scored 3 points).
In the round that the players scored (1, 1, 1, 1), Dipak must have scored 1 point.
In the round that the players scored (2, 2, - 2, - 2), Dipak must have scored 2 points (since the total points that Dipak scored in the first three rounds is 2).
From (3), Dipak must have scored 2 points in the first round, - 1 points in the second round and 1 point in the third round.
From this, we can fill the points for the first three rounds, as shown below
(Note that with this information, the first question of the set can be answered)
In the next three rounds, from (1) and (2), Arun must have scored 1 point, Bankim must have scored 1 point, Charu must have scored - 3 points and Dipak must have scored - 3 points.
The total points scored by the four players are - 4. This is possible if the total points scored by the four players in the three rounds are (0, 0, - 4) OR (4, - 4, - 4) in any order.
However, we know that Arun must have scored 3 points in one of these three rounds (from (4)). Hence, the total points scored by the players in this round must be 0.
Hence, the four players must have scored (0, 0, - 4) points in these three rounds. In one round the points scored by the players must be (3, - 1, - 1, - 1), with Arun scoring 3 points.
In the round in which the total points scored by the four players is 4, they must have scored ( - 1, - 1, - 1, - 1)
Since Bankim scored a total of 1 point in these three rounds, and he scored - 1 point and - 1 point in the two rounds mentioned above, he must have scored 3 points in the other third.
Hence, in the remaining round, the four players must have scored (3, - 1, - 1, - 1), with Bankim scoring 3 points.
However, with the given information, we cannot deduce the round number corresponding to the above rounds.
Hence, we get the following table:
All four players made identical bids in 2 rounds
Q.5. In how many rounds did Dipak gain exactly 1 point?
Ans: 1
Solution: From the given information, we can see that the points scored by the players in a round has the following possibilities:
HHHH: (-1, -1, -1, -1)
HHHL: (1, 1, 1, -3)
HHLL: (2, 2, -2, -2)
HLLL: (3, -1, -1, -1)
LLLL: (1, 1, 1, 1)
Also, the total points scored by the four players in a round can only be -4 or 0 or 4.
From (1), the total points scored by the four players combined in the first three rounds is 6 + 2 - 2 - 2 = 4.
Hence, in the first three rounds, the total points scored by the four players must be either (-4, 4, 4) OR (0, 0, 4), in any order.
Also, from (1), in the first three rounds, Arun scored 6 points. And from (2), Arun scored 7 points at the end of round 6. Hence, in the 4th , 5th and 6th rounds, he must have scored 1 point.
From (4), Arun scored 3 points in exactly 2 rounds.
These two rounds cannot both be among 4th , 5th and 6th rounds because he scored a net of only 1 point in these three rounds combined.
Hence, Arun must have scored 3 points in one round among 1st , 2nd and 3 rd rounds. If Arun scored 3 points in the first three rounds, then in that round, the total points scored by the four players combined must be 0 (in the case of HLLL).
Hence, the total points scored by the four players in the first three rounds must be (0, 0, 4). Among the first three rounds, in one round, the three players must have scored (3, -1, -1, -1), with Arun scoring 3 points.
Since in another round, the four players scored a total of 4 points, they must have bid LLLL (as it is the only case in which they can score 4 points in total). They must have scored (1, 1, 1, 1).
In the round that the players scored (3, - 1, - 1, - 1), Dipak must have scored - 1 points (since Arun scored 3 points).
In the round that the players scored (1, 1, 1, 1), Dipak must have scored 1 point.
In the round that the players scored (2, 2, - 2, - 2), Dipak must have scored 2 points (since the total points that Dipak scored in the first three rounds is 2).
From (3), Dipak must have scored 2 points in the first round, - 1 points in the second round and 1 point in the third round.
From this, we can fill the points for the first three rounds, as shown below
(Note that with this information, the first question of the set can be answered)
In the next three rounds, from (1) and (2), Arun must have scored 1 point, Bankim must have scored 1 point, Charu must have scored - 3 points and Dipak must have scored - 3 points.
The total points scored by the four players are - 4. This is possible if the total points scored by the four players in the three rounds are (0, 0, - 4) OR (4, - 4, - 4) in any order.
However, we know that Arun must have scored 3 points in one of these three rounds (from (4)). Hence, the total points scored by the players in this round must be 0.
Hence, the four players must have scored (0, 0, - 4) points in these three rounds. In one round the points scored by the players must be (3, - 1, - 1, - 1), with Arun scoring 3 points.
In the round in which the total points scored by the four players is 4, they must have scored ( - 1, - 1, - 1, - 1)
Since Bankim scored a total of 1 point in these three rounds, and he scored - 1 point and - 1 point in the two rounds mentioned above, he must have scored 3 points in the other third.
Hence, in the remaining round, the four players must have scored (3, - 1, - 1, - 1), with Bankim scoring 3 points.
However, with the given information, we cannot deduce the round number corresponding to the above rounds.
Hence, we get the following table:
Dipak gained exactly 1 point in 1 round
Q.6. In which of the following rounds, was Arun DEFINITELY the only player to bid Hi?
(a) First
(b) Fourth
(c) Third
(d) Second
Ans: d
Solution: From the given information, we can see that the points scored by the players in a round has the following possibilities:
HHHH: (-1, -1, -1, -1)
HHHL: (1, 1, 1, -3)
HHLL: (2, 2, -2, -2)
HLLL: (3, -1, -1, -1)
LLLL: (1, 1, 1, 1)
Also, the total points scored by the four players in a round can only be -4 or 0 or 4.
From (1), the total points scored by the four players combined in the first three rounds is 6 + 2 - 2 - 2 = 4.
Hence, in the first three rounds, the total points scored by the four players must be either (-4, 4, 4) OR (0, 0, 4), in any order.
Also, from (1), in the first three rounds, Arun scored 6 points. And from (2), Arun scored 7 points at the end of round 6. Hence, in the 4th , 5th and 6th rounds, he must have scored 1 point.
From (4), Arun scored 3 points in exactly 2 rounds.
These two rounds cannot both be among 4th , 5th and 6th rounds because he scored a net of only 1 point in these three rounds combined.
Hence, Arun must have scored 3 points in one round among 1st , 2nd and 3 rd rounds. If Arun scored 3 points in the first three rounds, then in that round, the total points scored by the four players combined must be 0 (in the case of HLLL).
Hence, the total points scored by the four players in the first three rounds must be (0, 0, 4). Among the first three rounds, in one round, the three players must have scored (3, -1, -1, -1), with Arun scoring 3 points.
Since in another round, the four players scored a total of 4 points, they must have bid LLLL (as it is the only case in which they can score 4 points in total). They must have scored (1, 1, 1, 1).
In the round that the players scored (3, - 1, - 1, - 1), Dipak must have scored - 1 points (since Arun scored 3 points).
In the round that the players scored (1, 1, 1, 1), Dipak must have scored 1 point.
In the round that the players scored (2, 2, - 2, - 2), Dipak must have scored 2 points (since the total points that Dipak scored in the first three rounds is 2).
From (3), Dipak must have scored 2 points in the first round, - 1 points in the second round and 1 point in the third round.
From this, we can fill the points for the first three rounds, as shown below
(Note that with this information, the first question of the set can be answered)
In the next three rounds, from (1) and (2), Arun must have scored 1 point, Bankim must have scored 1 point, Charu must have scored - 3 points and Dipak must have scored - 3 points.
The total points scored by the four players are - 4. This is possible if the total points scored by the four players in the three rounds are (0, 0, - 4) OR (4, - 4, - 4) in any order.
However, we know that Arun must have scored 3 points in one of these three rounds (from (4)). Hence, the total points scored by the players in this round must be 0.
Hence, the four players must have scored (0, 0, - 4) points in these three rounds. In one round the points scored by the players must be (3, - 1, - 1, - 1), with Arun scoring 3 points.
In the round in which the total points scored by the four players is 4, they must have scored ( - 1, - 1, - 1, - 1)
Since Bankim scored a total of 1 point in these three rounds, and he scored - 1 point and - 1 point in the two rounds mentioned above, he must have scored 3 points in the other third.
Hence, in the remaining round, the four players must have scored (3, - 1, - 1, - 1), with Bankim scoring 3 points.
However, with the given information, we cannot deduce the round number corresponding to the above rounds.
Hence, we get the following table:
In the second round, Arun was the only player to bid Hi.
Instruction
A survey of 600 schools in India was conducted to gather information about their online teaching learning processes (OTLP). The following four facilities were studied.
F1: Own software for OTLP
F2: Trained teachers for OTLP
F3: Training materials for OTLP
F4: All students having Laptops
The following observations were summarized from the survey.
1. 80 schools did not have any of the four facilities – F1, F2, F3, F4.
2. 40 schools had all four facilities.
3. The number of schools with only F1, only F2, only F3, and only F4 was 25, 30, 26 and 20 respectively.
4. The number of schools with exactly three of the facilities was the same irrespective of which three were considered.
5. 313 schools had F2.
6. 26 schools had only F2 and F3 (but neither F1 nor F4).
7. Among the schools having F4, 24 had only F3, and 45 had only F2.
8. 162 schools had both F1 and F2.
9. The number of schools having F1 was the same as the number of schools having F4.
Q.7. What was the total number of schools having exactly three of the four facilities?
(a) 200
(b) 50
(c) 80
(d) 64
Ans: a
Solution: The given information can be represented in the following Venn diagram.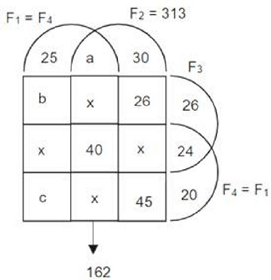
Given,
F2 = (a + x + 40 + x) + (30 + 26 + x + 45) = 313.
It is also given that F1 and F2 = a + x + 40 + x = 162.
Hence, 30 + 26 + x + 45 = 313 -162 = 151
Hence, x = 151 - (30 + 26 + 45) = 50
The number of schools that have exactly three facilities = 4x = 200
Q.8. What was the number of schools having facilities F2 and F4?
(a) 185
(b) 45
(c) 95
(d) 85
Ans: a
Solution: The number of schools having facilities F2 and F4 = 40 + x + 45 + x = 185
Q.9. What was the number of schools having only facilities F1 and F3?
Ans: 42
Solution: Only F1 and F3 = b
Given F1 = F4
25 + b + x + c + a + x + 40 + x
= 24+ 20 + x + 45 + 40 + x + x + c
Hence, a + b = 64
It is given that a + x + 40 + x = 162.
As x = 50, a = 22
Hence, only F1 and F3 = b = 64 - 22 = 42.
Q.10. What was the number of schools having only facilities F1 and F4?
Ans: 20
Solution: Only F1 and F4 = c
Exactly 1 + Exactly 2 + Exactly 3 + Exactly 4 = 600 - 80 = 520
(25 + 30 + 26 + 20) + Exactly 2 + 200 + 40 = 520
Hence, Exactly 2 = 179 = a + 24 + b + c + 26 + 45
As a = 22 and b = 42, c = only F1 and F4 = 20.
Instruction
Sixteen patients in a hospital must undergo a blood test for a disease. It is known that exactly one of them has the disease. The hospital has only eight testing kits and has decided to pool blood samples of patients into eight vials for the tests. The patients are numbered 1 through 16, and the vials are labelled A, B, C, D, E, F, G, and H. The following table shows the vials into which each patient’s blood sample is distributed.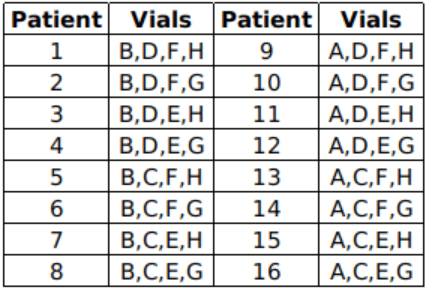
If a patient has the disease, then each vial containing his/her blood sample will test positive. If a vial tests positive, one of the patients whose blood samples were mixed in the vial has the disease. If a vial tests negative, then none of the patients whose blood samples were mixed in the vial has the disease.
Q.11. Suppose vial C tests positive and vials A, E and H test negative. Which patient has the disease?
(a) Patient 14
(b) Patient 2
(c) Patient 6
(d) Patient 8
Ans: c
Solution: If vial C tests positive vials A, E and H test negative. If vial C tests positive following patients can have disease.
Patient No. 5, 6, 7, 8, 13, 14, 15 & 16
If vials A, E & H test negative ⇒ following patients can't have disease
Patients who can’t have disease are:
Patient No. 5, 7, 8, 13, 14, 15 & 16 ⇒ Patient 6 must have disease
Q.12. Suppose vial A tests positive and vials D and G test negative. Which of the following vials should we test next to identify the patient with the disease?
(a) Vial E
(b) Vial H
(c) Vial C
(d) Vial B
Ans: a
Solution: If vial a tests positive, then following patients can have disease.
Patient No. 9,10,11,12,13,14,15,16 → (1)
Vials D \& G test negative
⇒ Following patients, can't have disease patients
No : -1, 2, 3, 4, 6, 8, 9,10,11,12,14, \&16 → (2)
From both 1 \&2, we ca say that patient No .13 or patient No. 15 can have disease.
Now we have eliminate or find out who among patient 13 or patient 15 has disease. So we should test vials E or F
Q.13. Which of the following combinations of test results is NOT possible?
(a) Vials A and G positive, vials D and E negative
(b) Vials B and D positive, vials F and H negative
(c) Vial B positive, vials C, F and H negative
(d) Vials A and E positive, vials C and D negative
Ans: d
Solution: If vials C & D test negative, that means none of the patients through 16 have diseases. But its given in the questions, that exactly one of the patients has disease. This is not possible
Q.14. Suppose one of the lab assistants accidentally mixed two patients' blood samples before they were distributed to the vials. Which of the following correctly represents the set of all possible numbers of positive test results out of the eight vials?
(a) {4,5}
(b) {5,6,7,8}
(c) {4,5,6,7,8}
(d) {4,5,6,7}
Ans: c
Solution: (i) Let’s assume one of the patients, patient 1 or patient 16 has disease and that patients blood is mixed with other them all 8 vials will test positive. Þ 8 has to be one of the answers.
(ii) If patient 2 and patients 16’s blood is mixed of one of them has disease then 7 of the 8 vials will test positive. So 7 has to be there in the option.
(iii) Let’s assume patient 1 has disease, if his blood is not mixed, then 4 vials will definitely show positive. So 4 also has to be there in answer. So the answer must definitely contain 4, 7 and 8
Instruction
XYZ organization got into the business of delivering groceries to home at the beginning of the last month. They have a two-day delivery promise. However, their deliveries are unreliable. An order booked on a particular day may be delivered the next day or the day after. If the order is not delivered at the end of two days, then the order is declared as lost at the end of the second day. XYZ then does not deliver the order, but informs the customer, marks the order as lost, returns the payment and pays a penalty for non-delivery.
The following table provides details about the operations of XYZ for a week of the last month. The first column gives the date, the second gives the cumulative number of orders that were booked up to and including that day. The third column represents the number of orders delivered on that day. The last column gives the cumulative number of orders that were lost up to and including that day.
It is known that the numbers of orders that were booked on the 11th, 12th, and 13th of the last month that took two days to deliver were 4, 6, and 8 respectively.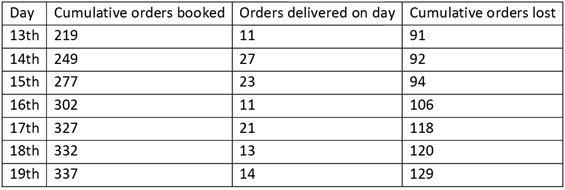
Q.15. Among the following days, the largest fraction of orders booked on which day was lost?
(a) 14th
(b) 13th
(c) 15th
(d) 16th
Ans: c
Solution: 14th day ⇒ 30 Booked ⇒ 12 loss ⇒ 12/30
13th day ⇒ 31 Booked ⇒ 2 loss = 2/31
16th day ⇒ 25 Booked ⇒ 2 loss ⇒ 2/25
15th day ⇒ 28 Booked ⇒ 12 loss ⇒ 12/28
The highest value is 12/28, on the 15th day.
Q.16. On which of the following days was the number of orders booked the highest?
(a) 13th
(b) 15th
(c) 12th
(d) 14th
Ans: a
Solution: Highest order Booked on 13th day.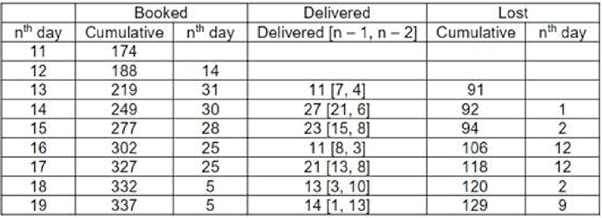
Q.17. The delivery ratio for a given day is defined as the ratio of the number of orders booked on that day which are delivered on the next day to the number of orders booked on that day which are delivered on the second day after booking. On which of the following days, was the delivery ratio the highest?
(a) 13th
(b) 16th
(c) 14th
(d) 15th
Ans: c
Solution: Delivery ratio = Next day / day after
a. 13th day ⇒ 21/8
b. 15th day ⇒ 8/8
c. 14th day ⇒ 15/3
d. 16th day ⇒ 13/10
The highest ratio is 15/3, on 14th day
Q.18. The average time taken to deliver orders booked on a particular day is computed as follows. Let the number of orders delivered the next day be x and the number of orders delivered the day after be y. Then the average time to deliver order is (x+2y)/(x+y). On which of the following days was the average time taken to deliver orders booked the least?
(a) 14th
(b) 16th
(c) 15th
(d) 13th
Ans: a
Solution:
The least is on the 14th day.
Instruction
A farmer had a rectangular land containing 205 trees. He distributed that land among his four daughters – Abha, Bina, Chitra and Dipti by dividing the land into twelve plots along three rows (X,Y,Z) and four Columns (1,2,3,4) as shown in the figure below:
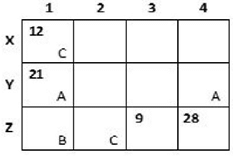
The plots in rows X, Y, Z contained mango, teak and pine trees respectively. Each plot had trees in non-zero multiples of 3 or 4 and none of the plots had the same number of trees. Each daughter got an even number of plots. In the figure, the number mentioned in top left corner of a plot is the number of trees in that plot, while the letter in the bottom right corner is the first letter of the name of the daughter who got that plot (For example, Abha got the plot in row Y and column 1 containing 21 trees). Some information in the figure got erased, but the following is known:
1. Abha got 20 trees more than Chitra but 6 trees less than Dipti.
2. The largest number of trees in a plot was 32, but it was not with Abha.
3. The number of teak trees in Column 3 was double of that in Column 2 but was half of that in Column 4.
4. Both Abha and Bina got a higher number of plots than Dipti.
5. Only Bina, Chitra and Dipti got corner plots.
6. Dipti got two adjoining plots in the same row.
7. Bina was the only one who got a plot in each row and each column.
8. Chitra and Dipti did not get plots which were adjacent to each other (either in row / column / diagonal).
9. The number of mango trees was double the number of teak trees.
Q.19. How many mango trees were there in total?
(a) 84
(b) 98
(c) 49
(d) 126
Ans: b
Solution: Let each plot in the grid be represented by its row label and column label. For example, (X, 2) represents the plot in row X and column 2.
From (8), Chitra and Dipti did not get plots which were adjacent to each other.
From the figure, we can see that Chitra has the plot (X, 1). Hence, Dipti cannot have the plots (X, 2) and (Y, 2).
Also, Chitra ha s the plot (Z, 2). Hence, Dipti cannot have the plots (Z, 3) and (Y, 3). From (6), Dipti has two adjoining plots in the same row. Hence, the only possibility for Dipti to have such plots is if she has the plots (X, 3) and (X, 4).
It is given that each daughter got an even number of plots. Also, from (4), Abha and Bina had a higher number of plots than Dipti.
Since Dipti already has 2 plots, Abha and Bina must have at least 4 plots each. Chitra already has 2 plots. Hence, Abha and Bina cannot have a higher n umber of plots. Hence, the number of plots that Abha, Bina, Chitra and Dipti must be 4, 4, 2 and 2, respectively.
We already know the positions of all the plots of Chitra and Dipti. Hence, the remaining plots must belong to Abha or Bina. From (5), the corner plot, (Z, 4) must belong to Bina. From (7), Bina got a plot in each row. In the first row, Chitra got (X, 1) and Dipti got (X, 3) and (X, 4). Hence, Bina must have gotten (X, 2). Bina has a total of 4 plots and we know the positions of three plots.
For Bina to have a plot in each row and each column, she must still have plot(s) in row Y and column 3. Since she can have only one more plot, she must have a plot at the intersection of this row and column.
Hence, Bina must have gotten the plot (Y, 3). A should have the remaining two plots, i.e., (Y, 2) and (Z, 3). Let the number of trees in (Y, 2) be a. From (3), the number of trees in (Y, 3) must be 2a and the number of trees in (Y, 4) must be 4a.
From (2), 4a cannot be more than 32 and since (Y, 4) is owned by Abha, it cannot be 32. Hence, a can be at most 7.
Also, a should be a multiple of 3 or 4. Hence, the possible values for a are 3, 4 and 6. However, a cannot be 3, since 4a will be 12 and (X, 1) has 12 trees (each plot has distinct number of trees).
Also, a cannot be 6, since 2a will be 12. Hence, a must be 4. The number of trees in (Y, 2), (Y, 3) and (Y, 4) must be 4, 8 and 16. The total number of trees in row Y is 21 + 4 + 8 + 16 = 49. From (9), the total number of trees in row X = 49 x 2 = 98 . The number of trees in row Z = 205 - 49 - 98 = 58. The total number of trees in the plots that Abha got is 21 + 4 + 16 + 9 = 50 (adding the trees in (Y, 1), (Y, 2), (Y, 4) and (Z, 3).
From (1), Chitra must have 30 trees and Dipti must have 56 trees. Since Chitra has 30 trees, and Chitra has 12 trees in (X, 1), there must be 18 trees in (Z, 2) (the only other plot that Chitra got).
The number of trees in (Z, 2), (Z, 3) and (Z, 4) are 18, 9 and 28 respectively. Since there must be 58 trees in row Z, the number of trees in (Z, 1) must be 3. The number of trees with Bina must be 205 - 50 - 56 - 30 = 69. Bina has 3 trees in (Z, 1), 8 trees in (Y, 3) and 28 trees in (Z, 4). In the last plot that Bina owns, i.e., in (X, 2), there must be 69 - 3 - 8 - 28 = 30 trees. In row X, in the plots that Dipti owns, (X, 3) and (X, 4), there must be a total of 56 trees. Since the maximum possible number of trees in only 32, the maximum possible number of trees in these two plots can be if they have 32 trees in one plot and 24 trees in the other plot (since 30 and 28 trees are already present in other plots). Hence, the plots (X, 3) and (X, 4) must have 32 and 24 trees in any order. The following table provides the distribution of plots and trees
The total number of mango trees are 98
Q.20. Which of the following is the correct sequence of trees received by Abha, Bina, Chitra and Dipti in that order?
(a) 50, 69, 30, 56
(b) 54, 57, 34, 60
(c) 44, 87, 24, 50
(d) 60, 39, 40, 66
Ans: a
Solution: Let each plot in the grid be represented by its row label and column label. For example, (X, 2) represents the plot in row X and column 2.
From (8), Chitra and Dipti did not get plots which were adjacent to each other.
From the figure, we can see that Chitra has the plot (X, 1). Hence, Dipti cannot have the plots (X, 2) and (Y, 2).
Also, Chitra ha s the plot (Z, 2). Hence, Dipti cannot have the plots (Z, 3) and (Y, 3). From (6), Dipti has two adjoining plots in the same row. Hence, the only possibility for Dipti to have such plots is if she has the plots (X, 3) and (X, 4).
It is given that each daughter got an even number of plots. Also, from (4), Abha and Bina had a higher number of plots than Dipti.
Since Dipti already has 2 plots, Abha and Bina must have at least 4 plots each. Chitra already has 2 plots. Hence, Abha and Bina cannot have a higher n umber of plots. Hence, the number of plots that Abha, Bina, Chitra and Dipti must be 4, 4, 2 and 2, respectively.
We already know the positions of all the plots of Chitra and Dipti. Hence, the remaining plots must belong to Abha or Bina. From (5), the corner plot, (Z, 4) must belong to Bina. From (7), Bina got a plot in each row. In the first row, Chitra got (X, 1) and Dipti got (X, 3) and (X, 4). Hence, Bina must have gotten (X, 2). Bina has a total of 4 plots and we know the positions of three plots.
For Bina to have a plot in each row and each column, she must still have plot(s) in row Y and column 3. Since she can have only one more plot, she must have a plot at the intersection of this row and column.
Hence, Bina must have gotten the plot (Y, 3). A should have the remaining two plots, i.e., (Y, 2) and (Z, 3). Let the number of trees in (Y, 2) be a. From (3), the number of trees in (Y, 3) must be 2a and the number of trees in (Y, 4) must be 4a.
From (2), 4a cannot be more than 32 and since (Y, 4) is owned by Abha, it cannot be 32. Hence, a can be at most 7.
Also, a should be a multiple of 3 or 4. Hence, the possible values for a are 3, 4 and 6. However, a cannot be 3, since 4a will be 12 and (X, 1) has 12 trees (each plot has distinct number of trees).
Also, a cannot be 6, since 2a will be 12. Hence, a must be 4. The number of trees in (Y, 2), (Y, 3) and (Y, 4) must be 4, 8 and 16. The total number of trees in row Y is 21 + 4 + 8 + 16 = 49. From (9), the total number of trees in row X = 49 x 2 = 98 . The number of trees in row Z = 205 - 49 - 98 = 58. The total number of trees in the plots that Abha got is 21 + 4 + 16 + 9 = 50 (adding the trees in (Y, 1), (Y, 2), (Y, 4) and (Z, 3).
From (1), Chitra must have 30 trees and Dipti must have 56 trees. Since Chitra has 30 trees, and Chitra has 12 trees in (X, 1), there must be 18 trees in (Z, 2) (the only other plot that Chitra got).
The number of trees in (Z, 2), (Z, 3) and (Z, 4) are 18, 9 and 28 respectively. Since there must be 58 trees in row Z, the number of trees in (Z, 1) must be 3. The number of trees with Bina must be 205 - 50 - 56 - 30 = 69. Bina has 3 trees in (Z, 1), 8 trees in (Y, 3) and 28 trees in (Z, 4). In the last plot that Bina owns, i.e., in (X, 2), there must be 69 - 3 - 8 - 28 = 30 trees. In row X, in the plots that Dipti owns, (X, 3) and (X, 4), there must be a total of 56 trees. Since the maximum possible number of trees in only 32, the maximum possible number of trees in these two plots can be if they have 32 trees in one plot and 24 trees in the other plot (since 30 and 28 trees are already present in other plots). Hence, the plots (X, 3) and (X, 4) must have 32 and 24 trees in any order. The following table provides the distribution of plots and trees
The correct sequence of trees received by Abha, Bina, Chitra and Dipti are 50, 69, 30, 56.
Q.21. How many pine trees did Chitra receive?
(a) 21
(b) 30
(c) 18
(d) 15
Ans: c
Solution: Let each plot in the grid be represented by its row label and column label. For example, (X, 2) represents the plot in row X and column 2.
From (8), Chitra and Dipti did not get plots which were adjacent to each other.
From the figure, we can see that Chitra has the plot (X, 1). Hence, Dipti cannot have the plots (X, 2) and (Y, 2).
Also, Chitra ha s the plot (Z, 2). Hence, Dipti cannot have the plots (Z, 3) and (Y, 3). From (6), Dipti has two adjoining plots in the same row. Hence, the only possibility for Dipti to have such plots is if she has the plots (X, 3) and (X, 4).
It is given that each daughter got an even number of plots. Also, from (4), Abha and Bina had a higher number of plots than Dipti.
Since Dipti already has 2 plots, Abha and Bina must have at least 4 plots each. Chitra already has 2 plots. Hence, Abha and Bina cannot have a higher n umber of plots. Hence, the number of plots that Abha, Bina, Chitra and Dipti must be 4, 4, 2 and 2, respectively.
We already know the positions of all the plots of Chitra and Dipti. Hence, the remaining plots must belong to Abha or Bina. From (5), the corner plot, (Z, 4) must belong to Bina. From (7), Bina got a plot in each row. In the first row, Chitra got (X, 1) and Dipti got (X, 3) and (X, 4). Hence, Bina must have gotten (X, 2). Bina has a total of 4 plots and we know the positions of three plots.
For Bina to have a plot in each row and each column, she must still have plot(s) in row Y and column 3. Since she can have only one more plot, she must have a plot at the intersection of this row and column.
Hence, Bina must have gotten the plot (Y, 3). A should have the remaining two plots, i.e., (Y, 2) and (Z, 3). Let the number of trees in (Y, 2) be a. From (3), the number of trees in (Y, 3) must be 2a and the number of trees in (Y, 4) must be 4a.
From (2), 4a cannot be more than 32 and since (Y, 4) is owned by Abha, it cannot be 32. Hence, a can be at most 7.
Also, a should be a multiple of 3 or 4. Hence, the possible values for a are 3, 4 and 6. However, a cannot be 3, since 4a will be 12 and (X, 1) has 12 trees (each plot has distinct number of trees).
Also, a cannot be 6, since 2a will be 12. Hence, a must be 4. The number of trees in (Y, 2), (Y, 3) and (Y, 4) must be 4, 8 and 16. The total number of trees in row Y is 21 + 4 + 8 + 16 = 49. From (9), the total number of trees in row X = 49 x 2 = 98 . The number of trees in row Z = 205 - 49 - 98 = 58. The total number of trees in the plots that Abha got is 21 + 4 + 16 + 9 = 50 (adding the trees in (Y, 1), (Y, 2), (Y, 4) and (Z, 3).
From (1), Chitra must have 30 trees and Dipti must have 56 trees. Since Chitra has 30 trees, and Chitra has 12 trees in (X, 1), there must be 18 trees in (Z, 2) (the only other plot that Chitra got).
The number of trees in (Z, 2), (Z, 3) and (Z, 4) are 18, 9 and 28 respectively. Since there must be 58 trees in row Z, the number of trees in (Z, 1) must be 3. The number of trees with Bina must be 205 - 50 - 56 - 30 = 69. Bina has 3 trees in (Z, 1), 8 trees in (Y, 3) and 28 trees in (Z, 4). In the last plot that Bina owns, i.e., in (X, 2), there must be 69 - 3 - 8 - 28 = 30 trees. In row X, in the plots that Dipti owns, (X, 3) and (X, 4), there must be a total of 56 trees. Since the maximum possible number of trees in only 32, the maximum possible number of trees in these two plots can be if they have 32 trees in one plot and 24 trees in the other plot (since 30 and 28 trees are already present in other plots). Hence, the plots (X, 3) and (X, 4) must have 32 and 24 trees in any order. The following table provides the distribution of plots and trees
The number of pine trees received by Chitra = 18
Q.22. Who got the plot with the smallest number of trees and how many trees did that plot have?
(a) Dipti, 6 trees
(b) Bina, 4 trees
(c) Abha, 4 trees
(d) Bina, 3 trees
Ans: d
Solution: Let each plot in the grid be represented by its row label and column label. For example, (X, 2) represents the plot in row X and column 2.
From (8), Chitra and Dipti did not get plots which were adjacent to each other.
From the figure, we can see that Chitra has the plot (X, 1). Hence, Dipti cannot have the plots (X, 2) and (Y, 2).
Also, Chitra ha s the plot (Z, 2). Hence, Dipti cannot have the plots (Z, 3) and (Y, 3). From (6), Dipti has two adjoining plots in the same row. Hence, the only possibility for Dipti to have such plots is if she has the plots (X, 3) and (X, 4).
It is given that each daughter got an even number of plots. Also, from (4), Abha and Bina had a higher number of plots than Dipti.
Since Dipti already has 2 plots, Abha and Bina must have at least 4 plots each. Chitra already has 2 plots. Hence, Abha and Bina cannot have a higher n umber of plots. Hence, the number of plots that Abha, Bina, Chitra and Dipti must be 4, 4, 2 and 2, respectively.
We already know the positions of all the plots of Chitra and Dipti. Hence, the remaining plots must belong to Abha or Bina. From (5), the corner plot, (Z, 4) must belong to Bina. From (7), Bina got a plot in each row. In the first row, Chitra got (X, 1) and Dipti got (X, 3) and (X, 4). Hence, Bina must have gotten (X, 2). Bina has a total of 4 plots and we know the positions of three plots.
For Bina to have a plot in each row and each column, she must still have plot(s) in row Y and column 3. Since she can have only one more plot, she must have a plot at the intersection of this row and column.
Hence, Bina must have gotten the plot (Y, 3). A should have the remaining two plots, i.e., (Y, 2) and (Z, 3). Let the number of trees in (Y, 2) be a. From (3), the number of trees in (Y, 3) must be 2a and the number of trees in (Y, 4) must be 4a.
From (2), 4a cannot be more than 32 and since (Y, 4) is owned by Abha, it cannot be 32. Hence, a can be at most 7.
Also, a should be a multiple of 3 or 4. Hence, the possible values for a are 3, 4 and 6. However, a cannot be 3, since 4a will be 12 and (X, 1) has 12 trees (each plot has distinct number of trees).
Also, a cannot be 6, since 2a will be 12. Hence, a must be 4. The number of trees in (Y, 2), (Y, 3) and (Y, 4) must be 4, 8 and 16. The total number of trees in row Y is 21 + 4 + 8 + 16 = 49. From (9), the total number of trees in row X = 49 x 2 = 98 . The number of trees in row Z = 205 - 49 - 98 = 58. The total number of trees in the plots that Abha got is 21 + 4 + 16 + 9 = 50 (adding the trees in (Y, 1), (Y, 2), (Y, 4) and (Z, 3).
From (1), Chitra must have 30 trees and Dipti must have 56 trees. Since Chitra has 30 trees, and Chitra has 12 trees in (X, 1), there must be 18 trees in (Z, 2) (the only other plot that Chitra got).
The number of trees in (Z, 2), (Z, 3) and (Z, 4) are 18, 9 and 28 respectively. Since there must be 58 trees in row Z, the number of trees in (Z, 1) must be 3. The number of trees with Bina must be 205 - 50 - 56 - 30 = 69. Bina has 3 trees in (Z, 1), 8 trees in (Y, 3) and 28 trees in (Z, 4). In the last plot that Bina owns, i.e., in (X, 2), there must be 69 - 3 - 8 - 28 = 30 trees. In row X, in the plots that Dipti owns, (X, 3) and (X, 4), there must be a total of 56 trees. Since the maximum possible number of trees in only 32, the maximum possible number of trees in these two plots can be if they have 32 trees in one plot and 24 trees in the other plot (since 30 and 28 trees are already present in other plots). Hence, the plots (X, 3) and (X, 4) must have 32 and 24 trees in any order. The following table provides the distribution of plots and trees
Bina got the plot with the smallest number of trees, which had 3 trees
Q.23. Which of the following statements is NOT true?
(a) Dipti got 56 mango trees.
(b) Bina got 32 pine trees.
(c) Chitra got 12 mango trees.
(d) Abha got 41 teak trees.
Ans: b
Solution: Let each plot in the grid be represented by its row label and column label. For example, (X, 2) represents the plot in row X and column 2.
From (8), Chitra and Dipti did not get plots which were adjacent to each other.
From the figure, we can see that Chitra has the plot (X, 1). Hence, Dipti cannot have the plots (X, 2) and (Y, 2).
Also, Chitra ha s the plot (Z, 2). Hence, Dipti cannot have the plots (Z, 3) and (Y, 3). From (6), Dipti has two adjoining plots in the same row. Hence, the only possibility for Dipti to have such plots is if she has the plots (X, 3) and (X, 4).
It is given that each daughter got an even number of plots. Also, from (4), Abha and Bina had a higher number of plots than Dipti.
Since Dipti already has 2 plots, Abha and Bina must have at least 4 plots each. Chitra already has 2 plots. Hence, Abha and Bina cannot have a higher n umber of plots. Hence, the number of plots that Abha, Bina, Chitra and Dipti must be 4, 4, 2 and 2, respectively.
We already know the positions of all the plots of Chitra and Dipti. Hence, the remaining plots must belong to Abha or Bina. From (5), the corner plot, (Z, 4) must belong to Bina. From (7), Bina got a plot in each row. In the first row, Chitra got (X, 1) and Dipti got (X, 3) and (X, 4). Hence, Bina must have gotten (X, 2). Bina has a total of 4 plots and we know the positions of three plots.
For Bina to have a plot in each row and each column, she must still have plot(s) in row Y and column 3. Since she can have only one more plot, she must have a plot at the intersection of this row and column.
Hence, Bina must have gotten the plot (Y, 3). A should have the remaining two plots, i.e., (Y, 2) and (Z, 3). Let the number of trees in (Y, 2) be a. From (3), the number of trees in (Y, 3) must be 2a and the number of trees in (Y, 4) must be 4a.
From (2), 4a cannot be more than 32 and since (Y, 4) is owned by Abha, it cannot be 32. Hence, a can be at most 7.
Also, a should be a multiple of 3 or 4. Hence, the possible values for a are 3, 4 and 6. However, a cannot be 3, since 4a will be 12 and (X, 1) has 12 trees (each plot has distinct number of trees).
Also, a cannot be 6, since 2a will be 12. Hence, a must be 4. The number of trees in (Y, 2), (Y, 3) and (Y, 4) must be 4, 8 and 16. The total number of trees in row Y is 21 + 4 + 8 + 16 = 49. From (9), the total number of trees in row X = 49 x 2 = 98 . The number of trees in row Z = 205 - 49 - 98 = 58. The total number of trees in the plots that Abha got is 21 + 4 + 16 + 9 = 50 (adding the trees in (Y, 1), (Y, 2), (Y, 4) and (Z, 3).
From (1), Chitra must have 30 trees and Dipti must have 56 trees. Since Chitra has 30 trees, and Chitra has 12 trees in (X, 1), there must be 18 trees in (Z, 2) (the only other plot that Chitra got).
The number of trees in (Z, 2), (Z, 3) and (Z, 4) are 18, 9 and 28 respectively. Since there must be 58 trees in row Z, the number of trees in (Z, 1) must be 3. The number of trees with Bina must be 205 - 50 - 56 - 30 = 69. Bina has 3 trees in (Z, 1), 8 trees in (Y, 3) and 28 trees in (Z, 4). In the last plot that Bina owns, i.e., in (X, 2), there must be 69 - 3 - 8 - 28 = 30 trees. In row X, in the plots that Dipti owns, (X, 3) and (X, 4), there must be a total of 56 trees. Since the maximum possible number of trees in only 32, the maximum possible number of trees in these two plots can be if they have 32 trees in one plot and 24 trees in the other plot (since 30 and 28 trees are already present in other plots). Hence, the plots (X, 3) and (X, 4) must have 32 and 24 trees in any order. The following table provides the distribution of plots and trees
Bina did not 32 pine trees. She got 31 pine trees
Q.24. Which column had the highest number of trees?
(a) 2
(b) 3
(c) Cannot be determined
(d) 4
Ans: d
Solution: Let each plot in the grid be represented by its row label and column label. For example, (X, 2) represents the plot in row X and column 2.
From (8), Chitra and Dipti did not get plots which were adjacent to each other.
From the figure, we can see that Chitra has the plot (X, 1). Hence, Dipti cannot have the plots (X, 2) and (Y, 2).
Also, Chitra ha s the plot (Z, 2). Hence, Dipti cannot have the plots (Z, 3) and (Y, 3). From (6), Dipti has two adjoining plots in the same row. Hence, the only possibility for Dipti to have such plots is if she has the plots (X, 3) and (X, 4).
It is given that each daughter got an even number of plots. Also, from (4), Abha and Bina had a higher number of plots than Dipti.
Since Dipti already has 2 plots, Abha and Bina must have at least 4 plots each. Chitra already has 2 plots. Hence, Abha and Bina cannot have a higher n umber of plots. Hence, the number of plots that Abha, Bina, Chitra and Dipti must be 4, 4, 2 and 2, respectively.
We already know the positions of all the plots of Chitra and Dipti. Hence, the remaining plots must belong to Abha or Bina. From (5), the corner plot, (Z, 4) must belong to Bina. From (7), Bina got a plot in each row. In the first row, Chitra got (X, 1) and Dipti got (X, 3) and (X, 4). Hence, Bina must have gotten (X, 2). Bina has a total of 4 plots and we know the positions of three plots.
For Bina to have a plot in each row and each column, she must still have plot(s) in row Y and column 3. Since she can have only one more plot, she must have a plot at the intersection of this row and column.
Hence, Bina must have gotten the plot (Y, 3). A should have the remaining two plots, i.e., (Y, 2) and (Z, 3). Let the number of trees in (Y, 2) be a. From (3), the number of trees in (Y, 3) must be 2a and the number of trees in (Y, 4) must be 4a.
From (2), 4a cannot be more than 32 and since (Y, 4) is owned by Abha, it cannot be 32. Hence, a can be at most 7.
Also, a should be a multiple of 3 or 4. Hence, the possible values for a are 3, 4 and 6. However, a cannot be 3, since 4a will be 12 and (X, 1) has 12 trees (each plot has distinct number of trees).
Also, a cannot be 6, since 2a will be 12. Hence, a must be 4. The number of trees in (Y, 2), (Y, 3) and (Y, 4) must be 4, 8 and 16. The total number of trees in row Y is 21 + 4 + 8 + 16 = 49. From (9), the total number of trees in row X = 49 x 2 = 98 . The number of trees in row Z = 205 - 49 - 98 = 58. The total number of trees in the plots that Abha got is 21 + 4 + 16 + 9 = 50 (adding the trees in (Y, 1), (Y, 2), (Y, 4) and (Z, 3).
From (1), Chitra must have 30 trees and Dipti must have 56 trees. Since Chitra has 30 trees, and Chitra has 12 trees in (X, 1), there must be 18 trees in (Z, 2) (the only other plot that Chitra got).
The number of trees in (Z, 2), (Z, 3) and (Z, 4) are 18, 9 and 28 respectively. Since there must be 58 trees in row Z, the number of trees in (Z, 1) must be 3. The number of trees with Bina must be 205 - 50 - 56 - 30 = 69. Bina has 3 trees in (Z, 1), 8 trees in (Y, 3) and 28 trees in (Z, 4). In the last plot that Bina owns, i.e., in (X, 2), there must be 69 - 3 - 8 - 28 = 30 trees. In row X, in the plots that Dipti owns, (X, 3) and (X, 4), there must be a total of 56 trees. Since the maximum possible number of trees in only 32, the maximum possible number of trees in these two plots can be if they have 32 trees in one plot and 24 trees in the other plot (since 30 and 28 trees are already present in other plots). Hence, the plots (X, 3) and (X, 4) must have 32 and 24 trees in any order. The following table provides the distribution of plots and trees
Column 4 has the highest number of trees
|
5 videos|385 docs|204 tests
|




















