Class 10 Exam > Class 10 Notes > Mathematics (Maths) Class 10 > RD Sharma Solutions: Pair of Linear Equations in Two Variables - 1
Pair of Linear Equations in Two Variables - 1 RD Sharma Solutions | Mathematics (Maths) Class 10 PDF Download
Exercise 3.1
Q.1. Akhila went to a fair in her village. She wanted to enjoy rides on the Giant Wheel and play Hoopla (a game in which you throw a rig on the items kept in the stall, and if the ring covers any object completely you get it). The number of times she played Hoopla is half the number of rides she had on the Giant Wheel. Each ride costs Rs 3, and a game of Hoopla costs Rs 4. If she spent Rs 20 in the fair, represent this situation algebraically and graphically. Sol: The pair of equations formed is:
Solution.
The pair of equations formed is:
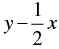
i.e., x - 2y = 0 ....(1)
3x + 4y = 20 ....(2)
Let us represent these equations graphically. For this, we need at least two solutions for each equation. We give these solutions in Table
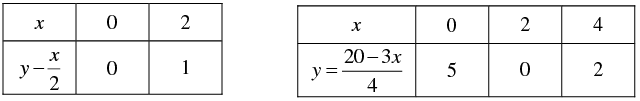
Recall from Class IX that there are infinitely many solutions of each linear equation. So each of you choose any two values, which may not be the ones we have chosen. Can you guess why we have chosen x =O in the first equation and in the second equation? When one of the variables is zero, the equation reduces to a linear equation is one variable, which can be solved easily. For instance, putting x =O in Equation (2), we get 4y = 20 i.e.,
y = 5. Similarly, putting y =O in Equation (2), we get 3x = 20 ..,
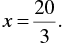 But as
But as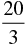 is not an integer, it will not be easy to plot exactly on the graph paper. So, we choose y = 2 which gives x = 4, an integral value.
is not an integer, it will not be easy to plot exactly on the graph paper. So, we choose y = 2 which gives x = 4, an integral value.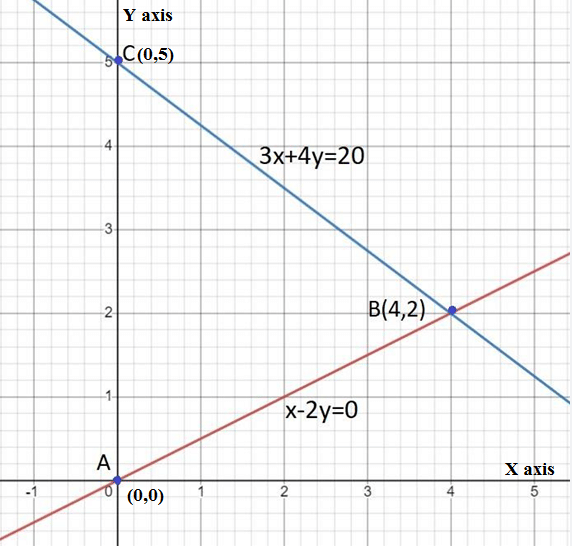 Plot the points A (O, O) , B (2,1) and P (O,5), Q (4,12), corresponding to the draw the lines AB and PQ, representing the equations x - 2 y = O and 3x + 4y= 20, as shown in figure In fig., observe that the two lines representing the two equations are intersecting at the point (4,2),
Plot the points A (O, O) , B (2,1) and P (O,5), Q (4,12), corresponding to the draw the lines AB and PQ, representing the equations x - 2 y = O and 3x + 4y= 20, as shown in figure In fig., observe that the two lines representing the two equations are intersecting at the point (4,2),Q.2. Aftab tells his daughter, “Seven years ago, I was seven times as old as you were then. Also, three years from now, I shall be three times as old as you will be.” Isn't this interesting? Represent this situation algebraically and graphically.
Sol: Let the present age of Aftab and his daughter be x and y respectively. Seven years ago.
Age of Ahab = x - 7
Age of his daughter y - 7
According to the given condition.
(x - 7) = 7(y - 7)
⇒ x - 7 = 7y - 49
⇒ x - 7y = -42
Three years hence
Age of Aftab = x + 3
Age of his daughter = y + 3
According to the given condition,
(x + 3) = 3 (y + 3)
⇒ x+3 = 3y +9
⇒ x - 3y = 6
Thus, the given condition can be algebraically represented as
x - 7y = - 42
x - 3y = 6
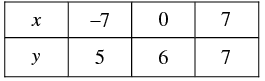
x - 7y = - 42 ⇒ x = -42 + 7y
Three solutions of this equation can be written in a table as follows:
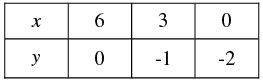
x - 3y = 6 ⇒ x = 6+3y
Three solutions of this equation can be written in a table as follows:
The graphical representation is as follows:
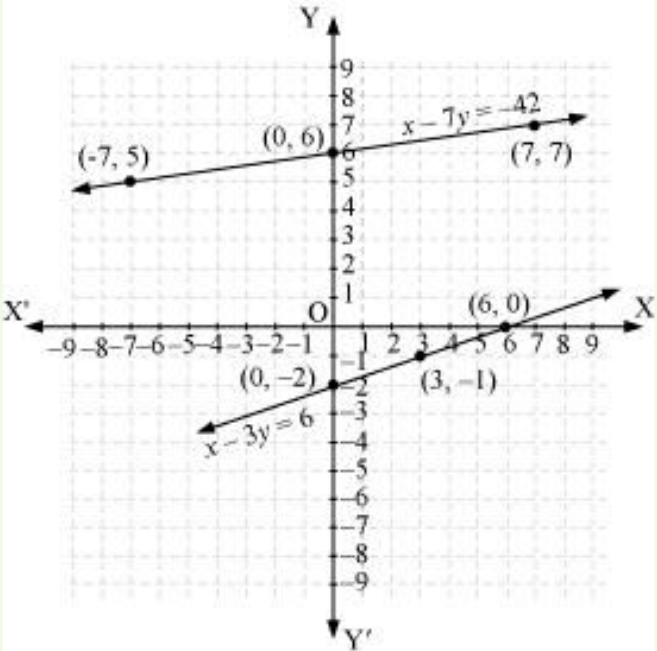 Concept insight In order to represent a given situation mathematically, first see what we need to find out in the problem. Here. Aftab and his daughter's present age needs to be found so, that the ages will be represented by variables z and y. The problem talks about their ages seven years ago and three years from now. Here, the words ’seven years ago’ mean we have to subtract 7 from their present ages. and ‘three years from now’ or three years hence means we have to add 3 to their present ages. Remember in order to represent the algebraic equations graphically the solution set of equations must be taken as whole numbers only for accuracy. The graph of the two linear equations will be represented by a straight line.
Concept insight In order to represent a given situation mathematically, first see what we need to find out in the problem. Here. Aftab and his daughter's present age needs to be found so, that the ages will be represented by variables z and y. The problem talks about their ages seven years ago and three years from now. Here, the words ’seven years ago’ mean we have to subtract 7 from their present ages. and ‘three years from now’ or three years hence means we have to add 3 to their present ages. Remember in order to represent the algebraic equations graphically the solution set of equations must be taken as whole numbers only for accuracy. The graph of the two linear equations will be represented by a straight line.Q.3. The path of a train A is given by the equation 3x + 4y - 12 = 0 and the path of another train B is given by the equation 6x + 8y - 48 = 0. Represent this situation graphically.
Sol:
The paths of two trains are given by the following pair of linear equations.
3x + 4 y -12 = 0 ...(1)
6x + 8 y - 48 = 0 ... (2)
To represent the above pair of linear equations graphically. We need two points on the line representing each equation. That is, we find two solutions of each equation as given below:
We have,
3x + 4 y -12 = 0
Putting y = 0, we get
3x + 4 x 0 - 12 = 0
⇒ 3x = 12
⇒
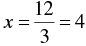
Putting x = 0, we get
3 x 0 + 4 y -12 = 0
⇒ 4y = 12
⇒
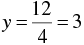
Thus, two solutions of equation 3x + 4y - 12 = 0 are ( 0, 3) and ( 4, 0 )
We have,
6x + 8y -48 = 0
Putting x = 0, we get
6 x 0 + 8 y - 48 = 0
⇒ 8y = 48
⇒
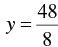
⇒ y = 6
Putting y = 0, we get
6x + 8 x 0 = 48 = 0
⇒ 6x = 48
⇒
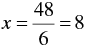
Thus, two solutions of equation 6 x + 8y - 48= 0 are ( 0, 6 ) and (8, 0 )
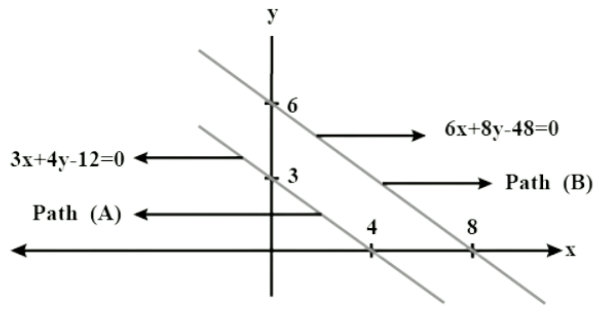 Clearly, two lines intersect at ( -1, 2 )Hence, x = -1,y = 2 is the solution of the given system of equations.
Clearly, two lines intersect at ( -1, 2 )Hence, x = -1,y = 2 is the solution of the given system of equations.Q.4. Gloria is walking along the path joining (— 2, 3) and (2, — 2), while Suresh is walking along the path joining (0, 5) and (4, 0). Represent this situation graphically.
Sol:
It is given that Gloria is walking along the path Joining (-2,3) and (2, -2), while Suresh is walking along the path joining (0,5) and (4,0).
 We observe that the lines are parallel and they do not intersect anywhere.
We observe that the lines are parallel and they do not intersect anywhere.Q.5. On comparing the ratios
 and without drawing them, find out whether the lines representing the following pairs of linear equations intersect at a point, are parallel or coincide:
and without drawing them, find out whether the lines representing the following pairs of linear equations intersect at a point, are parallel or coincide:(i) 5x- 4y + 8 = 0
7x + 6y - 9 = 0
(ii) 9x + 3y + 12 = 0
18x + 6y + 24 = 0
(iii) 6x - 3y + 10 = 0
2x - y + 9 = 0
Sol:
We have,
5x - 4 y + 8 = 0
7 x + 6 y - 9 = 0
Here,
a1 = 5, b1 = -4, c1 = 8
a2 = 7, b2 = 6, c2 = -9
We have,
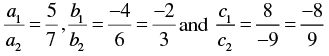
∴
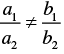
∴ Two lines are intersecting with each other at a point.
We have,
9 x + 3 y +12 = 0
18 + 6 y + 24 = 0
Here,
a1 = 9, b1 = 3, c1 = 12
a2 = 18, b2 = 6, c2 = 24
Now,
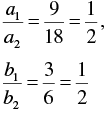
And
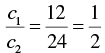
∴

∴ Both the lines coincide.
We have,
6 x - 3 y +10 = 0
2 x - y + 9 = 0
Here,
a1 = 6, b1 = -3, c1 = 10
a2 = 2, b2 = -1, c2 = 9
Now,
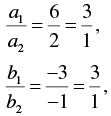
And
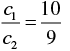
∴
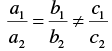
∴ The lines are parallel
Q.6. Given the linear equation 2x + 3y - 8 = 0, write another linear equation in two variables such that the geometrical representation of the pair so formed is:
(i) intersecting lines
(ii) parallel lines
(iii) coincident lines.
Sol:
We have,
2x + 3 y - 8 = 0
Let another equation of the line is
4x + 9 y - 4 = 0
Here,
a1 = 2, b1 = 3, c1 = -8
a2 = 4, b2 = 9, c2 = -4
Now,
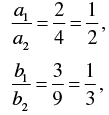
And
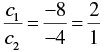
∴
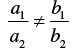
∴ 2x + 3 y - 8 = 0 and 4 x + 9 y - 4 = 0 intersect each other at one point.
Hence, required equation of line is 4 x + 9y - 4 = 0
We have,
2x + 3y -8 = 0
Let another equation of line is:
4x +6y -4 = 0
Here,
a1 = 2, b1 = 3, c1 = -8
a2 = 4, b2 = 6, c2 = -4
Now,
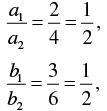
And
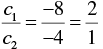
∴
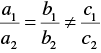
∴ Lines are parallel to each other.
Hence, the required equation of the line is 4 x + 6y - 4 = 0.
Q.7. The cost of 2kg of apples and 1 kg of grapes on a day was found to be Rs 160. After a month, the cost of 4kg of apples and 2kg of grapes is Rs 300. Represent the situation algebraically and geometrically.
Sol:
Let the cost of 1 kg of apples and 1 kg of grapes be Rs x and Rs y.
The given conditions can be algebraically represented as:
2 x + y = 160 and 4 x + 2 y = 300
2x + y = 160 ⇒ y = 160 - 2x
Three solutions of this equation can be written in a table as follows:
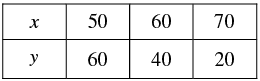
4x + 2y = 300 ⇒ y =
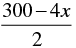
Three solutions of this equation can be written in a table as follows:

The graphical representation is as follows:
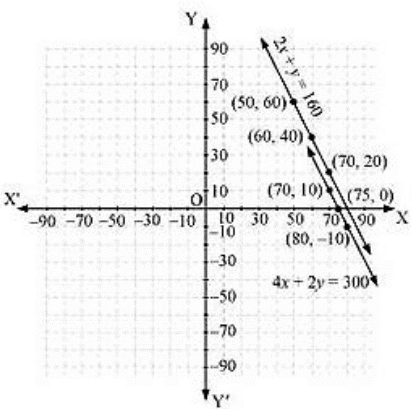 Concept insight: The cost of apples and grapes needs to be found so the cost of 1 kg apples and 1kg grapes will be taken as the variables from the given condition of collective cost of apples and grapes, a pair of linear equations in two variables will be obtained. Then In order to represent the obtained equations graphically, take the values of variables as whole numbers only. Since these values are Large so take the suitable scale.
Concept insight: The cost of apples and grapes needs to be found so the cost of 1 kg apples and 1kg grapes will be taken as the variables from the given condition of collective cost of apples and grapes, a pair of linear equations in two variables will be obtained. Then In order to represent the obtained equations graphically, take the values of variables as whole numbers only. Since these values are Large so take the suitable scale.
The document Pair of Linear Equations in Two Variables - 1 RD Sharma Solutions | Mathematics (Maths) Class 10 is a part of the Class 10 Course Mathematics (Maths) Class 10.
All you need of Class 10 at this link: Class 10
|
127 videos|584 docs|79 tests
|
FAQs on Pair of Linear Equations in Two Variables - 1 RD Sharma Solutions - Mathematics (Maths) Class 10
| 1. What are the methods to solve a pair of linear equations in two variables? |  |
Ans. There are three main methods to solve a pair of linear equations in two variables: the Graphical Method, the Substitution Method, and the Elimination Method. The Graphical Method involves plotting the equations on a graph to find the intersection point, which represents the solution. The Substitution Method entails solving one equation for one variable and substituting that value into the other equation. The Elimination Method involves adding or subtracting the equations to eliminate one variable, making it easier to solve for the other.
| 2. How do you check if a solution is correct for a pair of linear equations? |  |
Ans. To check if a solution is correct, substitute the values of the variables obtained from the solution back into both original equations. If both equations hold true (i.e., both sides of the equation are equal), then the solution is correct. If either equation does not hold true, then the solution is incorrect.
| 3. Can a pair of linear equations have no solution? |  |
Ans. Yes, a pair of linear equations can have no solution. This occurs when the lines represented by the equations are parallel, meaning they have the same slope but different y-intercepts. In such cases, the lines never intersect, indicating that there is no point (solution) that satisfies both equations simultaneously.
| 4. What is the graphical representation of a pair of linear equations? |  |
Ans. The graphical representation of a pair of linear equations is depicted as two lines on a coordinate plane. The point where the two lines intersect represents the solution to the equations. If the lines are parallel, they will never intersect, indicating no solution. If the lines overlap, they represent the same equation, resulting in infinitely many solutions.
| 5. How can we determine if a pair of linear equations has infinitely many solutions? |  |
Ans. A pair of linear equations has infinitely many solutions if they represent the same line on a graph. This occurs when the equations are equivalent, meaning that one can be derived from the other by multiplying or dividing by a non-zero constant. In such cases, every point on the line is a solution to both equations.
Related Searches





















