Pair of Linear Equations in Two Variables - 2 RD Sharma Solutions | Mathematics (Maths) Class 10 PDF Download
Exercise 3.2
Solve the following systems of equations graphically:
Q.1. x +y = 3
2x + 5y = 12
Sol:
We have
x + y = 3
2x + 5y = 12
Now, x +y = 3
When y = 0, we have
x = 3
When x = 0, we have
y = 3
Thus, we have the following table giving points on the line x +y = 3

Now,
2 + 5 y = 12
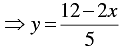
When x = 1, we have
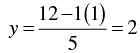
When x = -4, we have
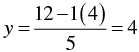
Thus, we have the following table giving points on the line 2 x + 5y = 12

Thus, we have the following table giving points on the line 2 x + 5y = 12
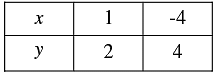
Graph of the equation x +y = 3 and 2 x + 5y = 12 :
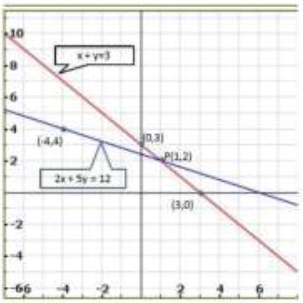
Clearly, two lines intersect at P (1, 2 ) .
Hence, x = 1,y = 2 is the solution of the given system of equations.
Q.2. x - 2 y = 5
2x + 3y = 10
Sol: We have
x - 2 y = 5
2 x + 3 y = 10
Now,
x - 2 y = 5
⇒ x = 5 + 2 y
When y = 0, we have
x = 5 + 2 x 0 = 5
When y = -2, we have
x = 5+ 2 x (-2) = 1
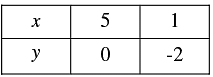
Thus, we have the following table giving points on the line x - 2y = 5
Now,
2x + 3y = 10
⇒ 2x = 10 - 3y
⇒
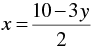
When y = 0, we have
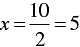
When y = 0, we have
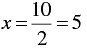
When y = 2, we have
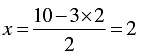
Thus, we have the following table giving points on the line 2x + 3y = 10
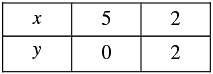
Graph of the equation x - 2 y = 5 and 2x + 3 y = 10 :
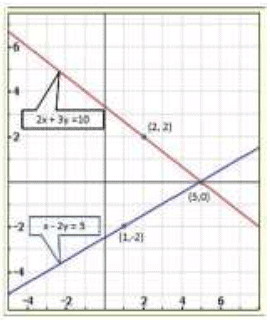
Clearly, two lines intersect at (5,0).
Hence, x = 5,y = 0 is the solution of the given system of equations.
Q.3. 3x + y + 1 = 0
2x - 3 y + 8 = 0
Sol:
We have,
3x + y +1 = 0
2x - 3 y + 8 = 0
Now,
3x + y + 1 = 0
⇒ y = - 1 - 3x
When x = 0, we have
y = -1
When x = - 1, we have
y = -1 - 3 x ( -1) = 2
Thus, we have the following table giving points on the line 3x + y + 1 = 0
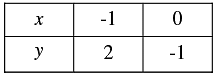
Now,
2 x - 3 y + 8 = 0
⇒ 2 x = 3 y - 8
⇒
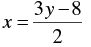
When y = 0, we have
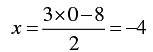
When y = 2, we have
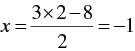
Thus, we have the following table giving points on the line 2 x - 3y + 8 = 0

Graph of the equation are:
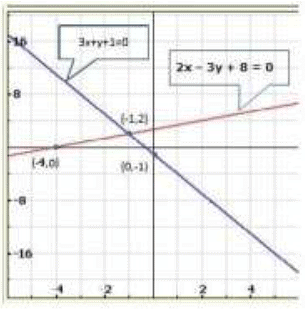
Clearly, two lines intersect at ( - 1, 2).
Hence, x = -1,y = 2 is the solution of the given system of equations.
Q.4. 2x + y - 3 = 0
2x - 3 y - 7 = 0
Sol:
We have
2x + y - 3 = 0
2x - 3 y - 7 = 0
Now,
2x + y - 3 = 0
⇒ y = 3 - 2x
When x = 0, we have
y = 3
When x = 1,we have
y =1
Thus, we have the following table giving points on the line 2x + y - 3 = 0

Now,
2x - 3y - 7 = 0
⇒ 3y = 2 x - 7
⇒
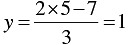
When x = 5, we have
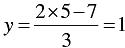
When x = 2, we have
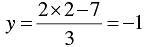
Thus, we have the following table giving points on the line 2 x - 3y - 7 = 0
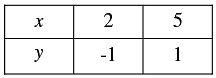
Graph of the given equation are
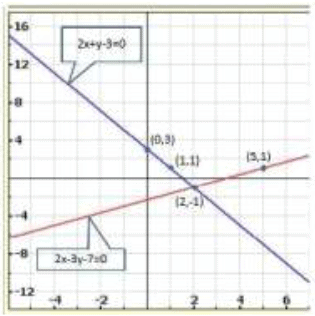
Clearly, two lines intersect at ( 2, -1).
Hence, x = 2,y = -1 is the solution of the given system of equations.
Q.5. x + y = 6
x - y = 2
Sol:
We have,
x + y = 6
x - y = 2
Now,
x + y = 6
⇒ y = 6 - x
When x = 2, we have
y = 4
When x = 3, we have
y = 3
Thus, we have the following table giving points on the line x +y = 6

Now,
x - y = 2
⇒ y = x - 2
When x = 0, we have
y = -2
When x = 2, we have
y = 0
Thus, we have the following table giving points on the line x -y = 6
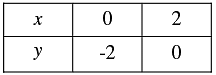
Graph of the given equation are
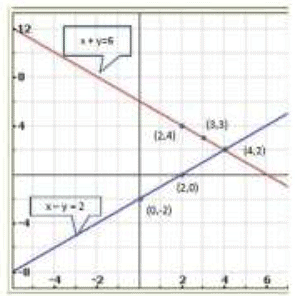
Clearly, two lines intersect at (4,2).
Hence, x = 4,y = 2 is the solution of the given system of equations.
Q.6. x - 2 y = 6
3x - 6 y = 0
Sol:
We have.
x - 2 y = 6
3x - 6 y = 0
Now,
x - 2 y = 6
⇒ x = 6 + 2 y
When y = -2, we have
x = 6 + 2x - 2 = 2
When y = -3, we have
x = 6 + 2x - 3 = 0
Thus, we have the following table giving points on the line x - 2 y = 6

Now,
3x - 6 y = 0
⇒ 3x = 6 y
⇒ x = 2 y
When y = 0, we have
x = 0
When y = 1, we have
x = 2
Thus, we have the following table giving points on the line 3x - 6y = 0
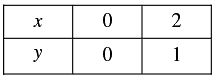
Graph of the given equation are
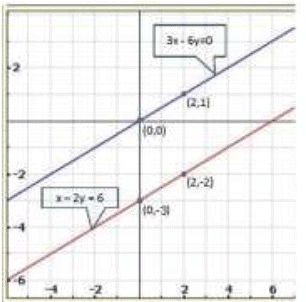
Clearly, two lines are parallel to each other. So, the two lines have no common point Hence, the given system of equations has no solution.
Q.7. x + y = 4
2 x - 3 y = 3
Sol:
We have.
x + y = 4
2x - 3 y = 3
Now,
x + y = 4
⇒ x = 4 - y
When y = 0, we have
x = 4
When y = 2, we have
x = 2
Thus, we have the following table giving points on the line x + y = 4

Now,
2 x - 3 y = 3
⇒ 2 x = 3 y + 3
⇒
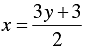
When y = 1, we have
x = 3
When y = -1, we have
x = 0
Thus, we have the following table giving points on the line 2 x - 3y = 3

Graph of the given equation are
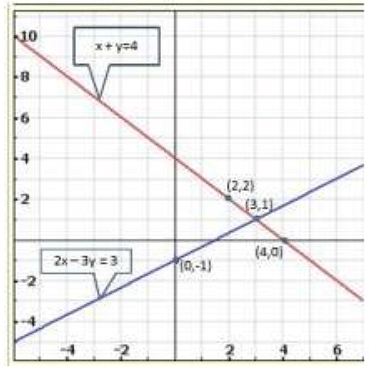
Clearly, two lines intersect at (3, 1).
Hence, x = 3,y = 1 is the solution of the given system of equations.
Q.8. 2 x + 3 y = 4
x - y + 3 = 0
Sol:
We have,
2x + 3 y = 4
x - y + 3 = 0
Now,
2 x + 3y = 4
⇒ 2x = 4 - 3y
⇒
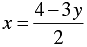
When y = 0, we have
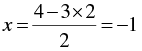
When y = 2, we have
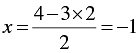
Thus, we have the following table giving points on the line 2 x + 3y = 4

Now,
x - y + 3 = 0
⇒ x = y - 3
When y = 3, we have
x = 0
When y = 4, we have
x = 1
Thus, we have the following table giving points on the line x - y + 3 = 0

Graph of the given equation are
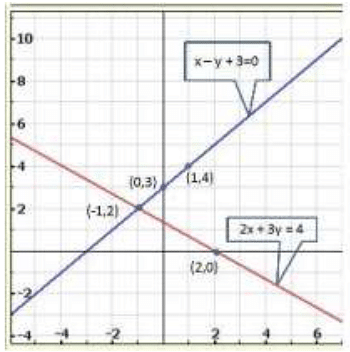
Clearly, two lines intersect at ( -1,2).
Hence, x = -1,y = 2 is the solution of the given system of equations.
Q.9. 2x - 3 y + 13 = 0
3x - 2 y + 12 = 0
Sol:
We have,
2x - 3 y +13 = 0
3x - 2 y +12 = 0
Now,
2 x - 3 y +13 = 0
⇒ 2x = 3y -13
⇒
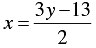
When y = 1, we have
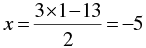
When y = 3, we have
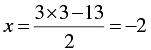
Thus, we have the following table giving points on the line 2 x - 3y + 13 = 0

Now,
3x - 2 y + 12 = 0
⇒ 3x = 2y - 12
⇒
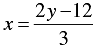
When y = 0, we have
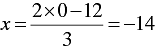
When y = 3, we have
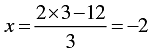
Thus, we have the following table giving points on the line 3 y - 2y + 12 = 0

Graph of the given equations are:
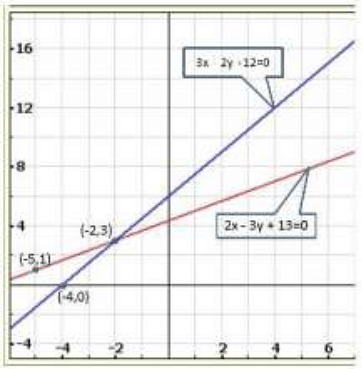
Clearly, two lines intersect at (-2, 3)
Hence, x = -2,y = 3 is the solution of the given system of equations.
Q.10. 2x + 3y + 5 = 0
3x + 2 y - 12 = 0
Sol:
We have,
2 x + 3 y + 5 = 0
3x + 2 y - 12 = 0
Now,
2 x + 3 y + 5 = 0
⇒ 2 x = -3 y - 5
=
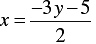
When y = 1, we have
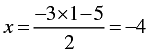
When y = 1, we have
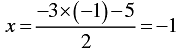
Thus, we have the following table giving points on the line 2 x + 3y + 5 = 0

Now,
3x - 2 y -12 = 0
⇒ 3x = 2y +12
⇒
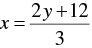
When y = 0, we have
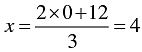
When y = 3, we have
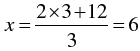
Thus we have the following table giving points on the line 3x - 2y - 12 = 0

Graph of the given equations are:
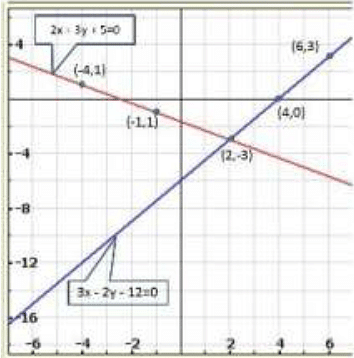
Clearly, two lines intersect at ( 2, -3) .
Hence, x = 2,y = -3 is the solution of the given system of equations.
Show graphically that each one of the following systems of equations has infinitely many solutions:
Q.11. 2 x + 3 y = 6
4x + 6 y = 12
Sol.
We have,
2 x + 3 y = 6
4x + 6 y = 12
Now,
2 x + 3 y = 6
⇒ 2 x = 6 - 3 y
⇒
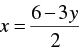
When y = 0, we have
x = 3
When y = 2, we have
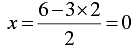
Thus, we have the following table giving points on the line 2x + 3y = 6
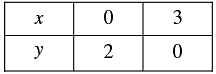
Now,
4 x + 6 y = 12
⇒ 4x = 12 - 6y
⇒
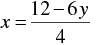
When y = 0, we have
x = 3
When y = 2, we have
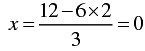
Thus, we have the following table giving points on the line 4 x + 6y = 12
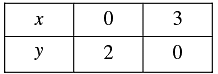
Graph of the given equations:
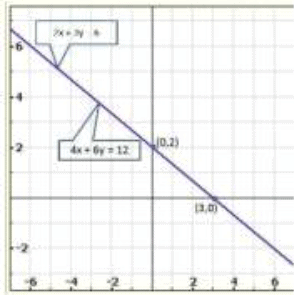
Thus, the graphs of the two equations are coincident.
Hence, the system of equations has infinitely many solutions.
Q.12. x - 2 y = 5
3x - 6 y = 15
Sol:
We have,
x - 2 y = 5
3x - 6 y = 15
Now,
x - 2 y = 5
⇒ x = 2 y + 5
When y = -1, we have
x = 2 (-1) + 5 = 3
When y = 0, we have
x = 2 x 0 + 5 = 5
Thus, we have the following table giving points on the line x - 2 y = 5

Now,
3x - 6 y = 15
⇒ 3x = 15 + 6y
⇒
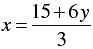
When y = -2, we have
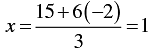
When y = -3, we have
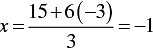
Thus, we have the following table giving points on the line 3x - 6y = 15

Graph of the given equations:
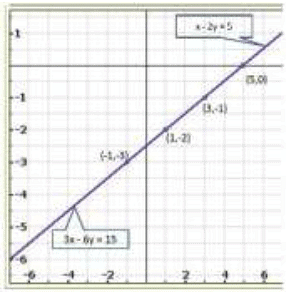
Q.13. 3x + y = 8
6 x + 2 y = 16
Sol.
We have,
3x + y = 8
6 x + 2 y = 16
Now,
3x + y = 8
⇒ y = 8 - 3x
When x = 2, we have
y = 8, -3x 2 = 2
When x = 3, we have
y = 8, -3x 3 = -1
Thus we have the following table giving points on the line 3 x + y = 8

Now,
6x + 2 y = 16
⇒ 2y = 16 - 6x
⇒
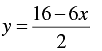
When x = 1, we have
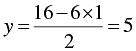
When x = 3, we have
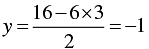
Thus we have the following table giving points on the line 6 x + 2y = 16

Graph of the given equations:
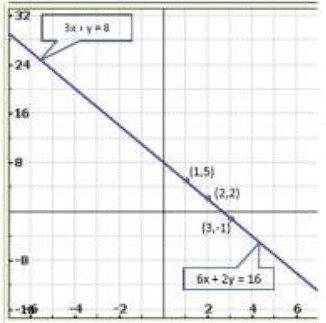
Thus, the graphs of the two equations are coincident.
Hence, the system of equations has infinitely many solutions,
Q.14. x + 2 y +11 = 0
3x + 6 y + 33 = 0
Sol:
We have,
x + 2 y +11 = 0
3x + 6 y + 33 = 0
Now,
x - 2 y +11 = 0
⇒ x = 2 y -11
When y = 5, we have
x = 2 x 5 - 11 = -1
When x = 4, we have
x = 2 x 4 -11 = - 3
Thus we have the following table giving points on the line x - 2y + 11 = 0

Now,
3x - 6 y + 33 = 0
⇒ 3x = 6 y - 33
⇒
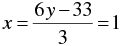
When y = 6, we have
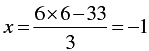
When y = 5, we have
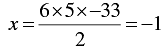
Thus we have the following table giving points on the line 3x + 6y + 33 = 0

Graph of the given equations:
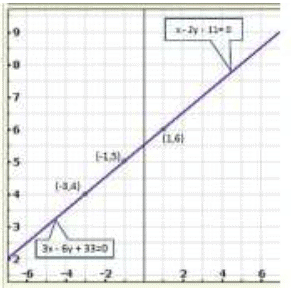
Thus, the graphs of the two equations are coincident,
Hence, the system of equations has infinitely many solutions,
Show graphically that each one of the following systems of equations is in-consistent (i.e., has no solution)
Q.15. 3x - 5 y = 20
6x -10 y = -40
Sol:
We have,
3x - 5 y = 20
6 x -10 y = -40
Now
⇒ 3x - 5 y = 20
⇒
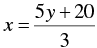
When y = -1, we have
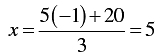
When y = -4, we have
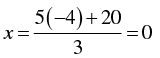
Thus we have the following table giving points on the line 3x - 5y = 20
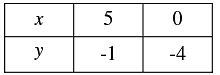
Now
6 x -10 y = -40
⇒ 6 x = -40 +10 y
⇒
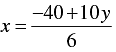
When y = 4, we have
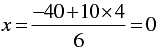
When y = 1, we have
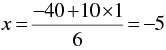
Thus we have the following table giving points on the line 6 x - 10y = -40


Graph of the given equations:
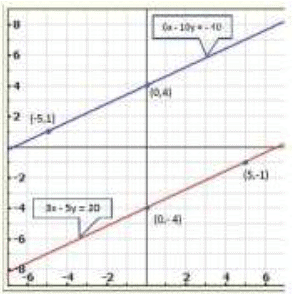
Clearly, there is no common point between these two lines
Hence, given system of equations is in-consistent.
Q.16. x - 2 y = 6
3x - 6 y = 0
Sol:
We have
x - 2 y = 6
3x - 6 y = 0
Now,
x - 2 y = 6
⇒ x = 6 + 2 y
When y = 0, we have
x = 6 + 2 x 0 = 6
When y = -2, we have
x = 6 + 2 x(-2) = 2
Thus, we have the following table giving points on the line x - 2 y = 6

Now,
3x - 6 y = 0
⇒ 3x = 6 y
⇒
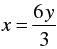
⇒ x = 2y
When y = 0, we have
x = 2 x 0 = 0
When y = 1, we have
x = 2 x 1 = 2
Thus, we have the following table giving points on the line 3x - 6y = 0

Graph of the given equations:
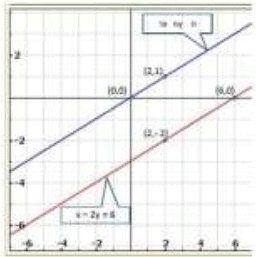
We find the lines represented by equations x - 2 y = 6 and 3 x - 6 y = 0are parallel. So, the two lines have no common point.
Hence, the given system of equations is in-consistent.
Q.17. 2 y - x = 9
6y - 3x = 21
Sol:
We have
2 y - x = 9
6 y - 3x = 21
Now,
2 y - x = 9
⇒ 2 y - 9 = x
⇒ x = 2 y - 9
When y = 3, we have
X = 2 X 3 - 9 = -3
When y = 4, we have
x = 2 x 4 - 9 = -1
Thus, we have the following table giving points on the line 2 x - x = 9

Now,
6 y - 3x = 21
⇒ 6y - 21 = 3x
⇒ 3x = 6y - 21
⇒
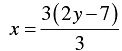
⇒ x = 2 y - 7
When y = 2, we have
x = 2 X 2 - 7 = -3
When y = 3, we have
x = 2 x 3 - 7 = -1
Thus, we have the following table giving points on the line 6 y - 3x = 21.

Graph of the given equations:
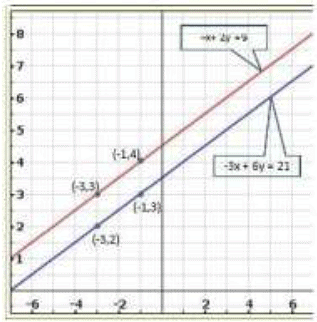
We find the lines represented by equations 2 y -x=9 and 6 y - 3x= 21 are parallel. So, the two lines have no common point.
Hence, the given system of equations is in-consistent.
Q.18. 3x - 4 y-1 = 0
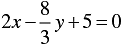
Sol.
We have
3x - 4 y-1 = 0
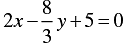
Now,
3x - 4 y-1 = 0
⇒ 3x = 1 + 4 y
⇒
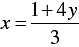
When y = 2, we have
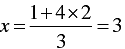
When y = -1, we have
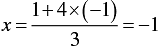
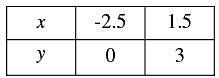
Thus, we have the following table giving points on the line 3x - 4y - 1 = 0.
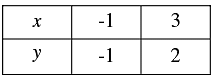
Now,
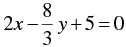
⇒
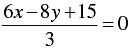
⇒ 6x - 8y + 15 = 0
⇒ 6 x = 8 y -15
⇒
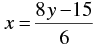
When y = 0, we have
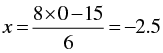
When y = 3, we have
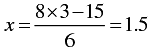
Thus, we have the following table giving points on the line
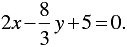
Graph of the given equations:
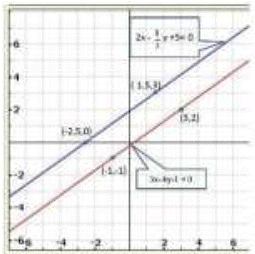
We find the lines represented by equations 3x - 4 y -1 = 0 and
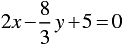 are parallel. So, the two lines have no common point.
are parallel. So, the two lines have no common point.Hence, the given system of equations is in-consistent.
Q.19. Determine graphically the vertices of the triangle, the equations of whose sides are given below:
2 y - x = 8
5 y - x = 14
(i) y - 2x = 1
y = x
y = 0
(ii) 3x + 3 y = 10
Sol:
We have
2 y - x = 8
5 y - x = 14
y - 2 x = 1
Now,
2 y - x = 8
⇒ 2 y = 8 = x
⇒ x = 2 y - 8
When y = 2, we have
x = 2 x 2 - 8 = -4
When y = 4, we have
x = 2 x 4 - 8 = 0
Thus, we have the following table giving points on the line 2 y - x = 8.
Now,
5 y - x = 14
⇒ 5y -14 = x
⇒ x = 5y -14
When y = 2, we have
x = 5 x 2-14 = 1
When y = 3, we have
x = 5 x 3-14 = 1
Thus, we have the following table giving points on the line 5 y - x = 14.
We have
y - 2 x = 1
⇒ y -1 = 2 x
⇒ 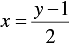
When y = 3, we have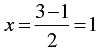
When y = -1, we have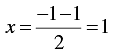
Thus, we have the following table giving points on the line y - 2x = 1.
Graph of the given equations: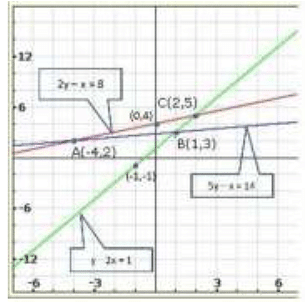
From the graph of the lines represented by the given equations, we observe that the lines taken in pairs intersect each other at points A (-4,2), B (1,3) and C (2,5)
Hence, the vertices of the triangle are A (-4,2), B (1,3) and C (2,5).
The given system of equations is y = x
y = 0
3x + 3 y = 10
We have, y = x
When x = 1,we have
y = 1
When x = -2,we have
y = -2
Thus, we have the following table points on the line y = x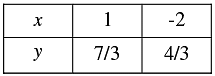
Graph of the given equation:
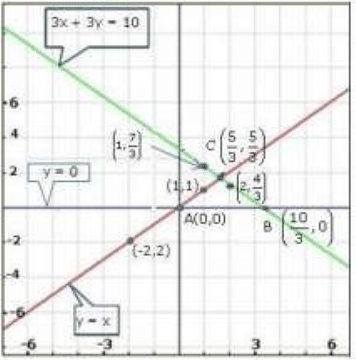
From the graph of the lines represented by the given equations, we observe that the lines
taken in pairs intersect each other at points A ( 0, 0 ), 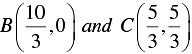
Hence, the required vertices of the triangle are A ( 0, 0 ), 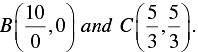
Q.20. Determine, graphically whether the system of equations x - 2y = 2, 4x - 2y = 5 is consistent or in-consistent.
Sol:
We have
x - 2 y = 2
4x - 2 y = 5
Now
x - 2 y = 2
⇒ x = 2 + 2 y
When y = 0, we have
x = 2 + 2 x 0 = 2
When y = -1, we have
x = 2 + 2 x(-1) = 0
Thus, we have the following table giving points on the line x - 2 y = 2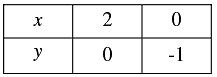
Now,
4 x - 2 y = 5
⇒ 4 x = 5 + 2 y
⇒ 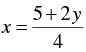
When y = 0, we have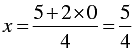
When y = 1, we have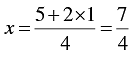
Thus, we have the following table giving points on the line 4 x - 2y = 5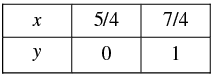
Graph of the given equations: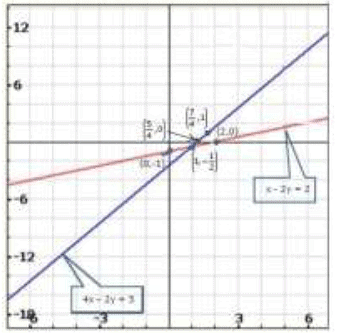
Clearly, the two lines intersect at (i!).
Hence, the system of equations is consistent.
Q.21. Determine, by drawing graphs, whether the following system of linear equations has a unique solution or not:
(i) 2x - 3y = 6, x + y = 1
(ii) 2y = 4x - 6, 2x = y + 3
Sol:
We have
2 x - 3 y = 6
x + y = 1
Now
2 x - 3 y = 6
⇒ 2 x = 6 + 3 y
When y = 0, we have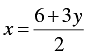
When y = -2, we have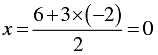
Thus, we have the following table giving points on the line 2 x - 3y= 6
Now,
x + y = 1
⇒ x = 1 - y
When y = 1, we have
x = 1-1 = 0
When y = 0, we have
x = 1- 0 = 1
Thus, we have the following table giving points on the line x + y = 1
Graph of the given equations: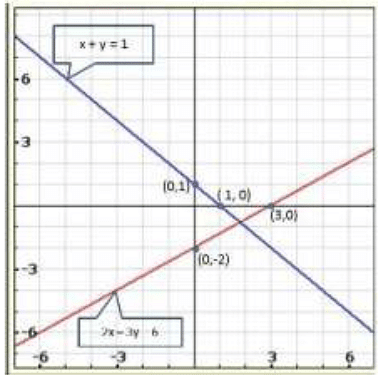
We have,
2 y = 4 x - 6
2x = y + 3
Now,
2 y = 4 x - 6
⇒ 2 y + 6 = 4 x
⇒ 4x = 2 y + 6
⇒ 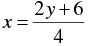
When y = -1, we have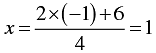
When y = 5, we have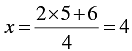
Thus, we have the following table giving points on the line 2 y = 4x - 6
Now,
2 x = y + 3
⇒ 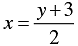
When y = 1, we have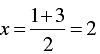
When y = 3, we have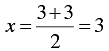
Thus, we have the following table giving points on the line 2 x =y +3
Graph of the given equations: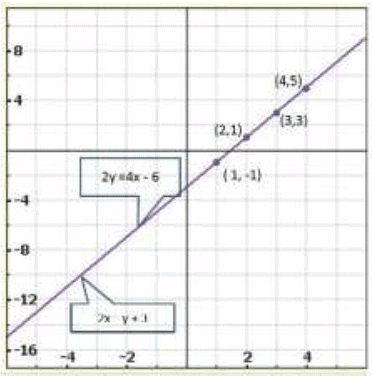
We find the graphs of the two equations are coincident,
∴ Hence, the system of equations has infinity many solutions
Q.22. Solve graphically each of the following systems of linear equations. Also find the coordinates of the points where the lines meet axis of y.
(i) 2x - 5 y + 4 = 0
2x+ y-8 = 0
(ii) 3x + 2 y = 12
5 x - 2 y = 4
(iii) 2 x + y -11 = 0
x - y-1 = 0
(iv) x + 2y - 7 = 0
2x - y - 4 = 0
(v) 3x + y - 5 = 0
2 x - y - 5 = 0
(vi) 2 x - y - 5 = 0
x - y - 3 = 0
Sol:
We have
2x - 5 y + 4 = 0
2x + y - 8 = 0
Now,
2 x - 5 y + 4 = 0
⇒ 2 x = 5 y - 4
⇒ 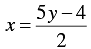
When y = 2, we have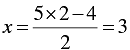
When y = 4, we have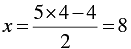
Thus, we have the following table giving points on the line 2 x - 5y + 4 = 0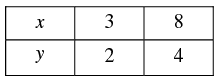
Now,
2 x + y - 8 = 0
⇒ 2 x = 8 - y
⇒ 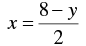
When y = 4, we have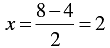
When y = 2, we have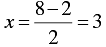
Thus, we have the following table giving points on the line 2 x - 5y + 4 = 0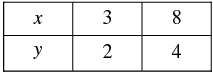
Graph of the given equations: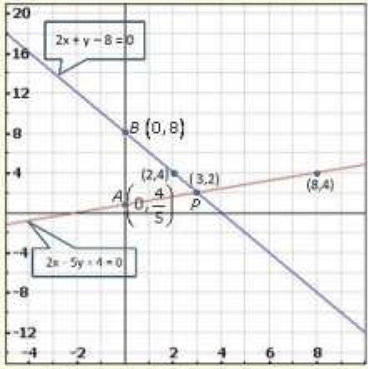
Clearly, two intersect at P (3,2).
Hence, x = 2, y = 3 is the solution of the given system of equations.
We also observe that the lines represented by 2X - 5y + 4 = 0 and 2x + y - 8 = 0 meet y - axis at 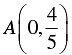 and B (0,8) respectively.
and B (0,8) respectively.
We have,
3x + 2y = 12
5 x - 2 y = 4
Now,
3x + 2 y = 12
⇒ 3x = 12 - 2 y
⇒ 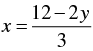
When y = 3, we have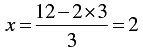
When y = -3, we have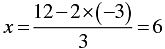
Thus, we have the following table giving points on the line 3x + 2y = 12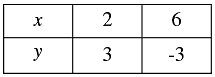
Now,
5x - 2 y = 4
⇒ 5x = 4 + 2 y
⇒ 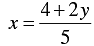
When y = 3, we have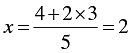
When y = -7, we have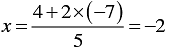
Thus, we have the following table giving points on the line 5x - 2y = 4
Graph of the given equation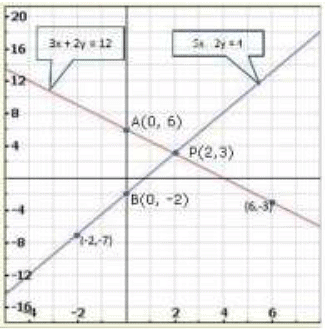
Clearly, two intersect at p (2,3).
Hence, x = 2, y = 3 is the solution of the given system of equations.
We also observe that the lines represented by 3x + 2y = 12 and 5x - 2y = 4 meet y-axis at A (0,6) and B (0, -2) respectively.
We have,
2 x + y -11 = 0
x - y-1 = 0
Now,
2 x + y -11 = 0
⇒ y = 11 - 2 x
When x = 4, we have
y = 11 - 2 x 4 = 3
When x = 5, we have
y = 11 - 2 x 5 = 1
Thus, we have the following table giving points on the line 2x + y -11 = 0
Now,
x - y -1 = 0
⇒ x -1 = y
⇒ y = x -1
When x = 2, we have
y = 2-1 = 1
When x = 3, we have
y = 3 -1 = 2
Thus, we have the following table giving points on the line x - y -1 = 0
Graph of the given equation
We have,
2 x + y -11 = 0
x - y-1 = 0
Now,
2 x + y -11 = 0
⇒ y = 11 - 2 x
When x = 4, we have
y = 11 - 2 x 4 = 3
When x = 5, we have
y = 11 - 2 x 5 = 1
Thus, we have the following table giving points on the line 2x + y -11 = 0
Now,
x - y -1 = 0
⇒ x -1 = y
⇒ y = x -1
When x = 2, we have
y = 2-1 = 1
When x = 3, we have
y = 3-1 = 2
Thus, we have the following table giving points on the line x - y -1 = 0
Graph of the given equations: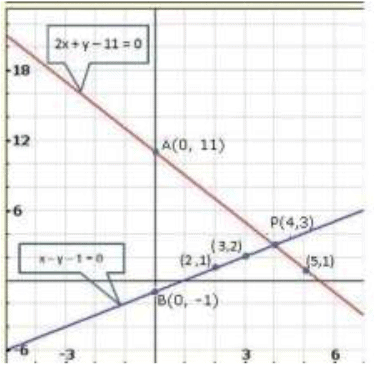
Clearly, two intersect at P (4,3).
Hence, x = 4, y = 3 is the solution of the given system of equations.
We also observe that the lines represented by 2x + y -11 = 0 and x - y -1 = 0 meet y-axis at, A (0,11) and B (0, -1) respectively.
We have, x + 2 y - 7 = 0
Now,
2 x - y - 4 = 0
x + 2 y - 7 = 0
x = 7 - 2 y
When
y = 1, x = 5
y = 2, x = 3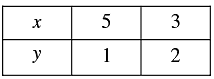
Also,
2 x - y - 4 = 0
y = 2 x - 4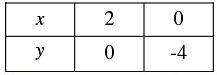
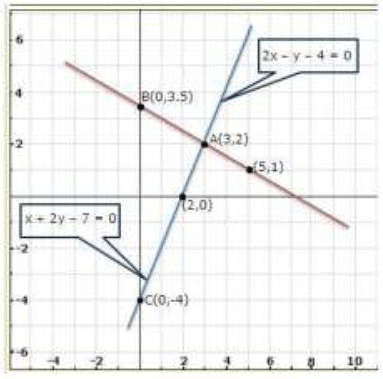
From the graph, the solution is A (3,2).
Also, the coordinates of the points where the lines meet the y-axis are B(0,3.5) and C(0,-4).
We have
3x + y - 5 = 0
2 x - y - 5 = 0
Now,
3x + y - 5 = 0
⇒ y = 5 - 3x
When x = 1,we have
y = 5, -3x1 = 2
When x = 2, we have
y = 5, -3x 2 = -1
Thus, we have the following table giving points on the line 3x + y - 5 = 0
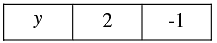
Now,
2 x - y - 5 = 0
⇒ 2 x - 5 = y
⇒ y = 2 x - 5
When x = 0, we have
y = -5
When x = 2, we have
y = 2 x 2 - 5 = -1
Thus, we have the following table giving points on the line 2 x - y - 5 = 0
Graph of the given equations: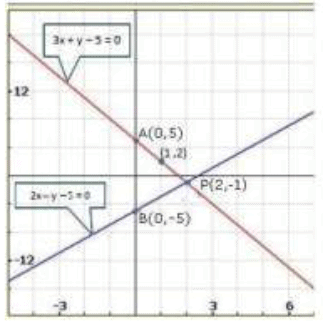
Clearly, two intersect at P (2, -1).
Hence, x = 2, y = -1 is the solution of the given system of equations.
We also observe that the lines represented by 3x + y -5 = 0 and 2x - y -5 = 0 meet y-axis at A (0,5) and 8 (0, -5) respectively.
We have,
2 x - y - 5 = 0
x - y - 3 = 0
Now,
2 x - y - 5 = 0
⇒ 2 x - 5 = y
⇒ y = 2 x - 5
When x = 1,we have
y = 2 x1 - 5 = -3
When x = 2, we have
y = 2 x 2 - 5 = -1
Thus, we have the following table giving points on the line 2x - y - 5 = 0
Now,
x - y - 3 = 0
⇒ x - 3 = y
⇒ y = x - 3
When x = 3, we have
y = 3 - 3 = 0
When x = 4, we have
y = 4 - 3 = 1
Thus, we have the following table giving points on the line x - y - 3 = 0
Graph of the given equations: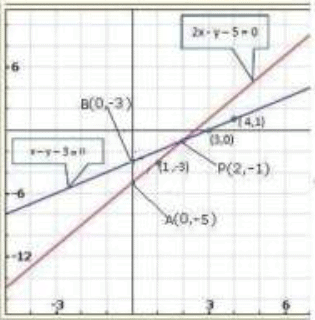
Clearly, two intersect at P (2, -1).
Hence, x = 2, y = —1 is the solution of the given system of equations?
We also observe that the lines represented by 2x — y—5 = 0 and x — y—3 = 0 meet y-axis at A(0, —5) and 8 (0, —3) respectively.
Q.23. Determine graphically the coordinates of the vertices of a triangle, the equations of whose sides are:
(i) y = x
y = 2 x
y + x = 6
y = x
(ii) 3 y = x
x + y = 8
Sol:
The system of the given equations is,
y = x
y = 2 x
y + x = 6
Now,
y = x
When x = 0, we have
y = 0
When x = -1,we have
y = -1
Thus, we have the following table:
We have
y = 2 x
When x = 0, we have
y = 2 x 0 = 0
When x = -1,we have
y = 2 (-1) = -2
Thus, we have the following table:
We have
y + x = 6
⇒ y = 6 - x
When x = 2, we have
y = 6 - 2 = 4
When x = 4, we have
y = 6 - 4 = 2
Thus, we have the following table:
Graph of the given system of equations: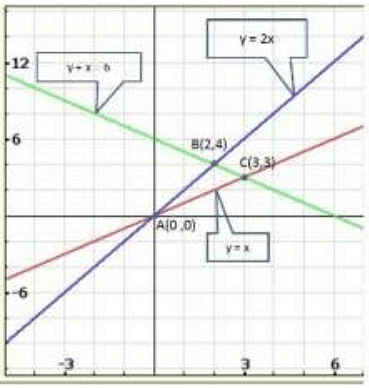
From the graph of the three equations, we find that the three lines taken in pairs intersect each other at points A(0,0),B(2,4) and C(3,3).
Hence, the vertices of the required triangle are (0,0), (2,4) and (3,3).
The system of the given equations is,
y = x
3 y = x
x + y = 8
Now,
y = x
⇒ x = y
When y = 0, we have
x = 0
When y = -3, we have
x = -3
Thus, we have the following table.
We have
3 y = x
⇒ x = 3 y
When y = 0, we have
x = 3x 0 = 0
When y = -1, we have
y = 3x(-1) = -3
Thus, we have the following table:
We have
x + y = 8
⇒ x = 8 - y
When y = 4, we have
x = 8 - 4 = 4
When y = 5, we have
x = 8 - 5 = 3
Thus, we have the following table:
Graph of the given system of equations: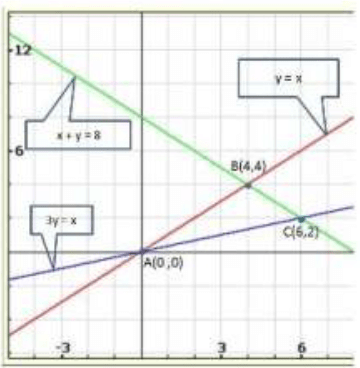
From the graph of the three equations, we find that the three lines taken in pairs intersect each other at points A(0,0), B(4,4) and C(6,2).
Hence, the vertices of the required triangle are (0,0), (44) and (6,2).
Q.24. Solve the following system of linear equations graphically and shade the region between the two lines and x-axis:
(i) 2x + 3 y = 12
x - y = 1
(ii) 3x + 2 y - 4 = 0
2 x - 3 y - 7 = 0
(iii) 3x + 2 y-11 = 0
2 x - 3 y +10 = 0
Ans.
Sol:
The system of given equations is
2x + 3 y = 12
x - y = 1
Now,
2 x + 3 y = 12
⇒ 2x = 12 - 3y
⇒ 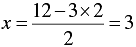
When y = 2, we have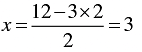
When y = 4, we have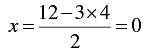
Thus, we have the following table:
We have,
x - y = 1
⇒ x = 1 + y
When y = 0, we have
x = 1
When y = 1,we have
x = 1 + 1 = 2
Thus, we have the following table:
Graph of the given system of equations: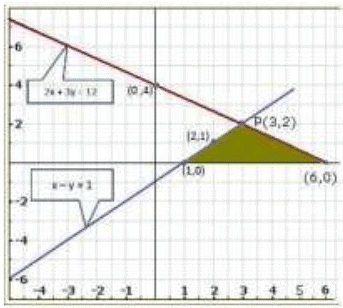
Clearly, the two lines intersect at P (3,2).
Hence, x = 3, y = 2 is the solution of the given system of equations. The system of the given equations is,
3x + 2 y - 4 = 0
2 x - 3 y - 7 = 0
Now,
3x + 2 y - 4 = 0
⇒ 3x = 4 - 2 y
⇒ 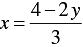
When y = 5, we have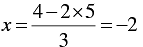
When y = 8, we have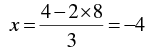
Thus, we have the following table:
We have,
2 x - 3 y - 7 = 0
⇒ 2 x = 3 y + 7
⇒ 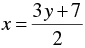
When y = 1, we have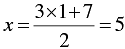
When y = -1, we have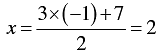
Thus, we have the following table:
Graph of the given system of equations: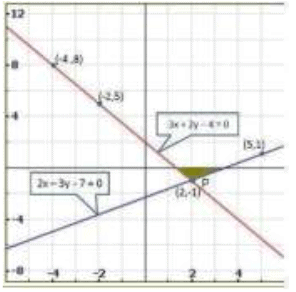
Clearly, the two lines intersect at P ( 2, -1) .
Hence, x = 2, y = -1 is the solution of the given system of equations.
The system of the given equations is,
3x + 2 y - 11 = 0
2x - 3 y +10 = 0
Now,
3x + 2 y - 11 = 0
⇒ 3x = 11 - 2 y
⇒ 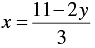
When y = 1, we have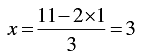
When y = 4, we have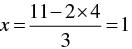
Thus, we have the following table:
We have,
2x - 3 y +10 = 0
⇒ 2 x = 3 y -10
⇒ 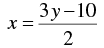
When y = 0, we have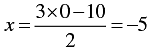
When y = 2, we have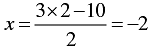
Thus, we have the following table:
Graph of the given system of equations: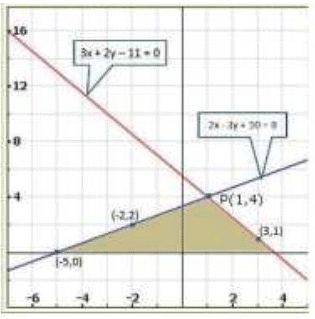
Clearly, the two lines intersect at P (1, 4 ) .
Hence, x = 1,y = 4 is the solution of the given system of equations
Q.25. Draw the graphs of the following equations on the same graph paper:
2x + 3 y = 12
x - y = 1
Sol:
The system of the given equations is
2x + 3 y = 12
x - y = 1
Now,
2 x + 3 y = 12
⇒ 2x = 12 - 3y
⇒ 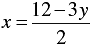
When y = 0, we have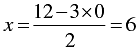
When y = 2, we have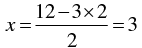
Thus, we have the following table: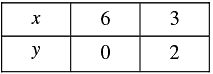
We have
x - y = 1
⇒ x = 1 + y
When y = 0, we have
x = 1
When y = -1, we have
x = 1-1 = 0
Thus, we have the following table:
Graph of the given system of equations: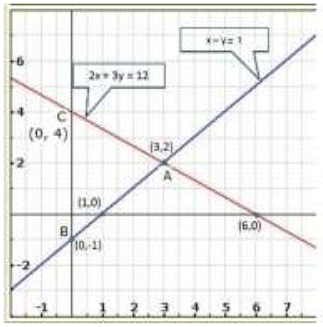
Clearly, the two lines intersect at A (3,2).
We also observe that the lines represented by the equations 2x + 3y = 12 and x - y = -1
meet y-axis at B (0,-1) and C (0,4).
Hence, the vertices of the required triangle are A(3,2), B(0,-1) and C(0,4).
Q.26. Draw the graphs of x — y + 1 = 0 and 3x + 2y — 12 = 0. Determine the coordinates of the vertices of the triangle formed by these lines and x- axis and shade the triangular area. Calculate the area bounded by these lines and x-axis.
Sol:
The given system of equations is
X - y + 1 = 0
3x + 2 y-12 = 0
Now,
x - y +1 = 0 ⇒ x = y -1 When y = 3, we have x = 3-1 = 2 When y = -1, we have x = -1 -1 = -2
Thus, we have the following table:
We have
3x + 2 y-12 = 0
⇒ 3x = 12 - 2 y
⇒ 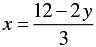
When y = 6, we have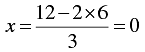
When y = 3, we have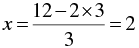
Thus, we have the following table:
Graph of the given system of equations: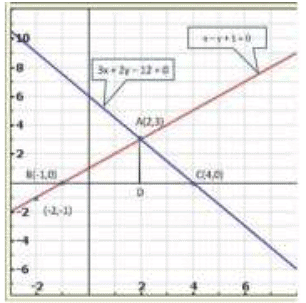
Clearly, the two lines intersect at A(2,3).
We also observe that the lines represented by the equations
x - y +1 = 0 and 3x + 2y -12 = Omeet x-axis at B (-1,0) and C (4,0) respectively.
Thus, x = 2, y = 3 is the solution of the given system of equations.
Draw AD perpendicular from A on x-axis.
Clearly, we have
AD = y - coordinate of point A (2,3)
⇒ AD = 3 and, BC = 4-(-1) = 4 +1 = 5
Q.27. Solve graphically the system of linear equations:
4 x - 3 y + 4 = 0
4 x + 3 y - 20 = 0
Find the area bounded by these lines and x-axis.
Sol:
The given system of equation is
4 x - 3 y + 4 = 0
4 x + 3 y - 20 = 0
Now,
4 x - 3 y + 4 = 0
⇒ 4 x = 3 y - 4
⇒ 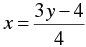
When y = 0, we have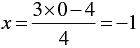
When y = 4, we have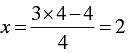
Thus, we have the following table:
We have
4 x + 3 y - 20 = 0
⇒ 4 x = 20 - 3 y
⇒ 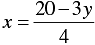
When y = 0, we have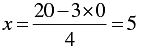
When y = 4, we have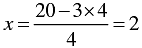
Thus, we have the following table:
Graph of the given system of equation: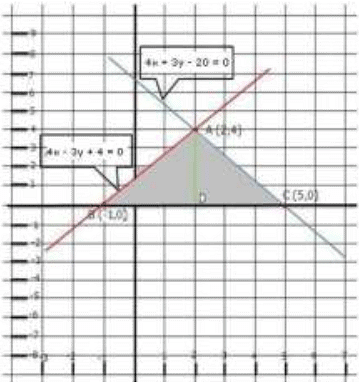
Clearly, the two lines intersect at A(2,4).Hence x = 2, y = 4is the solution of the given system of equations.
We also observe that the lines represented by the equations
4x - 3y + 4 = 0 and 4x + 3y-20 = 0 meet x-axis at B(-1,0) and C(5,0) respectively.
Thus, x = 2, y = 4 is the solution of the given system of equations.
Draw AD perpendicular from A on x-axis.
Clearly, we have
AD = y - coordinate of point A (2,4)
⇒ AD = 4 and, BC = 5-(-1) = 5 +1 = 6
∴ Area of the shaded region = Area of ΔABC
⇒ Area of the shaded region = 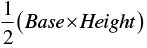
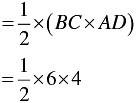
= 6 x 2
= 12 sq. units
∴ Area of shaded region = 12 sq. units
Q.28. Solve the following system of linear equations graphically:
3x + y -11 = 0
x - y -1 = 0
Shade the region bounded by these lines and y -axis. Also, find the area of the region bounded by these lines and y-axis.
Sol:
The given system of equation is
3x + y -11 = 0
x - y -1 = 0
Now,
3x + y -11 = 0
⇒ y = 11 - 3x
When x = 0, we have
y = 11 - 3x 0 = 11
When x = 3 we have
y = 11 - 3 x 3 = 2
Thus, we have the following table:
We have
x - y -1 = 0
⇒ x -1 = y
⇒ y = x -1
When x = 0, we have
y = 0 -1 = -1
When x = 3, we have
y = 3 - 1 = 2
Thus, we have the following table: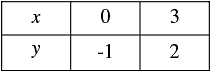
Graph of the given system of equations: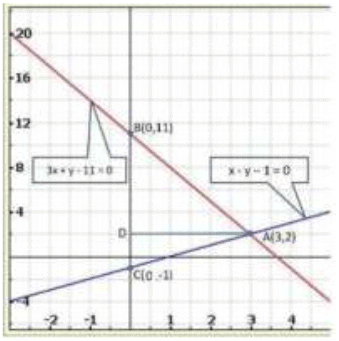
Clearly, the two lines intersect at A (32). Hence x = 3, y = 2 is the solution of the given system of equations.
We so observe that the lines represented by the equations 3x + y -11 = 0 and x - y -1 = 0 meet y-axis at B (0,11) and C (0,-1) respectively.
Thus, x = 3, y = 2 is the solution of the given system of equations.
Draw AD perpendicular from A on y-axis.
Clearly, we have
AD = x - coordinate of point A (3,2)
⇒ AD = 3 and, BC = 11 -(-1) = 11 +1 = 12
∴ Area of the shaded region = Area of ΔABC
⇒ Area of the shaded region = 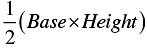
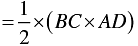
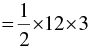
= 6 x 3
= 18 sq. units
∴ Area of the shaded region = 18 sq. units
Q.29. Solve graphically each of the following systems of linear equations. Also, find the coordinates of the points where the lines meet the axis of x in each system:
(i) 2 x - y = 2
4x - y = 8
(ii) 2 x - y = 2
4 x - y = 8
(iii) x + 2 y = 5
2 x - 3 y = -4
(iv) 2 x + 3 y = 8
x - 2 y = -3
Sol:
The given system of equation is
2 x - y = 2
4 x - y = 8
Now,
2 x + y = 2
⇒ 2 x = y + 2
⇒ 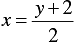
When y = 0, we have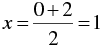
When y = 2, we have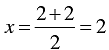
Thus, we have the following table:
We have,
4 x - y = 8
⇒ 4 x = y + 8
⇒ 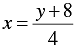
When y = 0, we have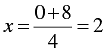
When y = -4 we have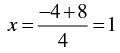
Thus, we have the following table: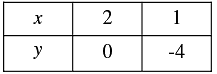
Graph of the given system of equations: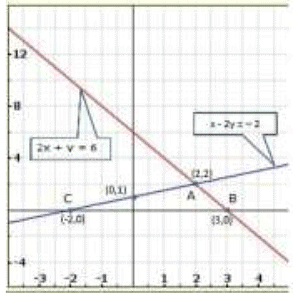
Clearly, the two lines intersect at A(2,2).Hence x = 2, y = 2is the solution of the given system of equations.
We so observe that the lines represented by the equations 2x + y = 6 and x - 2y = -2 meet x-axis at B (3,0) and C (-2,0) respectively.
The system of the given equations is
2 x + y = 6
x - 2 y = -2
Now,
2 x + y = 6
⇒ 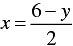
When y = 0, we have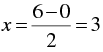
When y = 2, we have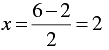
Thus, we have the following table: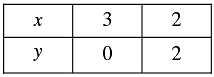
We have,
x - 2 y = -2
⇒ y - 2y - 2
When y = 0, we have
x = 2 x 0 - 2 = - 2
When y = 1,we have
x = 2 x1 - 2 = 0
Thus, we have the following table: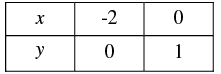
Graph of the given system of equations: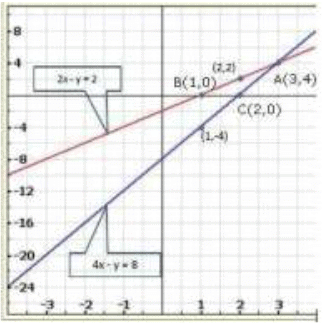
Clearly the two lines intersect at A (3,4). Hence x = 3, y = 4 is the solution of the given system of equations.
We so observe that the lines represented by the equations 2x - y = 2 and 4x - y = 8 meet x-axis at B (1,0) and C (2,0) respectively
The system of the given equations is
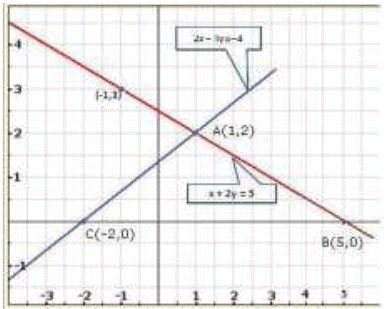
x + 2 y = 5
2 x - 3 y = -4
Now,
x + 2 y = 5
x = 5 - 2 y
When y = 2, we have
x = 5 - 2 x 2 = 1
When y = 3, we have
x = 5 - 2 x 3 = -1
Thus, we have the following table:
We have,
2 x - 3 y = -4
⇒ 2x = 3y - 4
⇒ 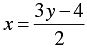
When y = 0, we have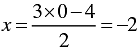
When y = 2, we have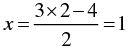
Thus, we have the following table:
Graph of the given system of equations: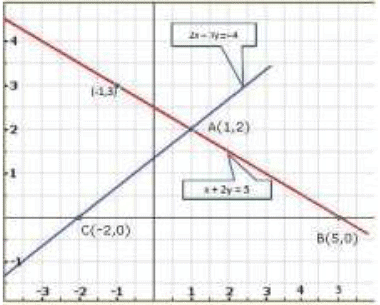
The given system of equation is
2 x + 3 y = 8
x - 2 y = -3
Now,
2 x + 3 y = 8
⇒ 2 x = 8 - 3 y
⇒ 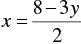
When y = 2, we have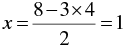
When y = 4, we have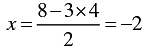
Thus, we have the following table:
We have,
x - 2 y = -3
⇒ x = 2y - 3
When y = 0, we have
x = 2 x 0 - 3 = -3
When y = 1,we have
x = 2 x 1 -3 = -1
Thus, we have the following table: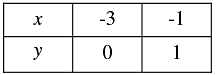
Graph of the given system of equations: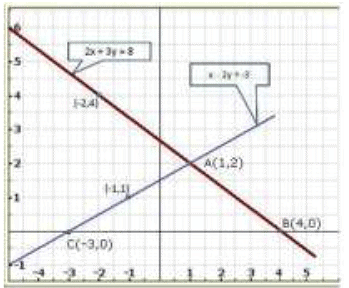
Clearly, the two lines intersect at A(1,2).Hence x = 1, y = 2 is the solution of the given system of equations.
We also observe that the lines represented by the equations 2x + 3y = 8 and x - 2y = -3 meet x-axis at B (4,0) and C (-3,0) respectively.
Q.30. Draw the graphs of the following equations:
2 x - 3 y + 6 = 0
2x + 3 y -18 = 0
y - 2 = 0
Find the vertices of the triangle so obtained. Also, find the area of the triangle.
Sol:
The given system of equation is
2 x - 3 y + 6 = 0
2x + 3 y -18 = 0
y - 2 = 0
Now,
2 x - 3 y + 6 = 0
⇒ 2 x = 3 y - 6
⇒ 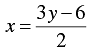
When y = 0, we have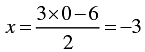
When y = 2, we have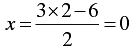
Thus, we have the following table: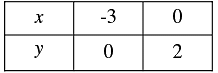
We have,
2x + 3 y -18 = 0
⇒ 2x = 18 - 3y
⇒ 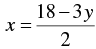
When y = 2, we have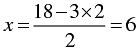
When y = 6, we have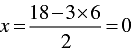
Thus, we have the following table: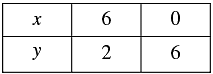
We have
y - 2 = 0
⇒ y = -2
Graph of the given system of equations: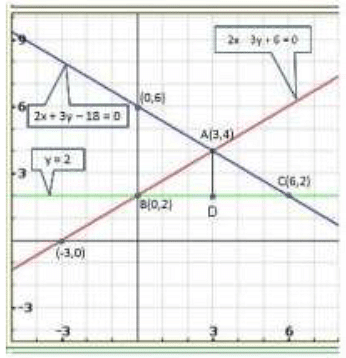
From the graph of the three equations, we find that the three lines taken in pairs intersect each other at points A(3,4), B(0,2) and C(6,2).
Hence, the vertices of the required triangle are (3,4), (0,2) and (6,2).
From graph, we have
AD = 4 - 2 = 2
BC = 6 - 0 = 6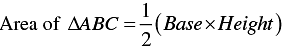
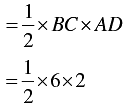
= 6 sq. units
∴ Area of ΔABC = 6 sq.units
Q.31. Solve the following system of equations graphically:
2 x - 3 y + 6 = 0
2 x + 3 y -18 = 0
Also, find the area of the region bounded by these two lines and y-axis.
Sol:
The given system of equation is
2 x - 3 y + 6 = 0
2 x + 3 y -18 = 0
Now,
2 x - 3 y + 6 = 0
⇒ 2 x + 6 = 3 y
⇒ 3 y = 2 x + 6
⇒ 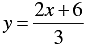
When x = 0, we have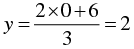
When x = -3, we have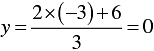
Thus, we have the following table: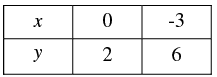
Graph of the given system of equations: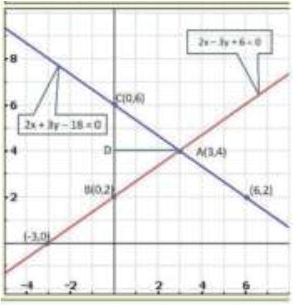
Clearly, the two lines intersect at A (3,4) .Hence, x = 3, y = 4 is the solution of the given system of equations.
We also observe that the lines represented by the equations
2x-3y + 6 = 0 and 2x + 3y-18 = 0 meet y-axis at B(0,2) and C(0,6)respectively.
Thus, x = 3, y = 4 is the solution of the given system of equations.
Draw AD perpendicular from A on y-axis.
Clearly, we have,
AD = x - coordinate of point A (3,4)
⇒ AD = 3 and, BC = 6 - 2 = 4
Area of the shaded region = Area of ΔABC
Area of the shaded region 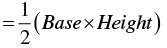
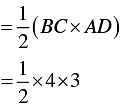
= 2 x 3
= 6 sq. units
∴ Area of the region bounded by these two lines and y-axis is 6 sq. units.
Q.32. Solve the following system of linear equations graphically:
4x - 5 y - 20 = 0
3x + 5 y -15 = 0
Determine the vertices of the triangle formed by the lines representing the above equation and the y-axis.
Sol:
The given system of equation is
4 x - 5 y - 20 = 0
3x + 5 y -15 = 0
Now,
4 x - 5 y - 20 = 0
⇒ 4 x = 5 y + 20
⇒ 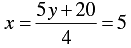
When y = 0, we have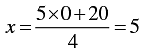
When y = -4, we have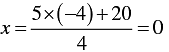
Thus, we have the following table: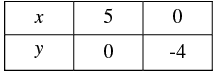
We have,
3x + 5 y -15 = 0
⇒ 3x = 15 - 5y
⇒ 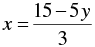
When y = 0, we have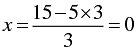
When y = 3, we have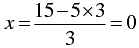
Thus, we have the following table: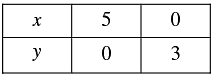
Graph of the given system of equations:
Clearly, the two lines intersect at 4(5,0).Hence, x-5, y-0is the solution of the given system of equations.
We also find that the two lines represented by the equations
4x-5y-20 = 0 and 3x+5y-15 = 0meet y-axis at B(0,-4) and C(0,3) respectively,
∴ The vertices of the required triangle are (5,0), (0, -4) and (0,3).
Q.33. Draw the graphs of the equations 5x - y = 5 and 3x - y = 3. Determine the co-ordinates of the vertices of the triangle formed by these lines and y-axis. Calculate the area of the triangle so formed.
Sol:
5x - y = 5 ⇒ y = 5x - 5
Three solutions of this equation can be written in a table as follows: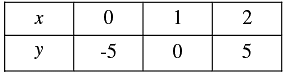
3x - y = 3 ⇒ y = 3x - 3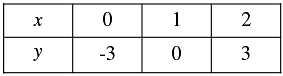
The graphical representation of the two lines will be as follows: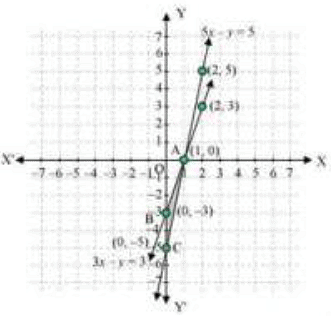
It can be observed that the required triangle is ΔABC.
The coordinates of its vertices are A (1,0), B (0, - 3), C (0, -5).
Concept insight: In order to find the coordinates of the vertices of the triangle so formed. Find the points where the two lines intersects the y-axis and also where the two lines intersect each other. Here, note that the coordinates of the intersection of lines with y-axis is taken and not with x-axis, this is became the question says to find the triangle formed by the two lines and the y-axis.
Q.34. Form the pair of linear equations in the following problems, and find their solution graphically:
(i) 10 students of class X took part in Mathematics quiz. If the number of girls is 4 more than the number of boys, find the number of boys and girls who took part in the quiz.
(ii) 5 pencils and 7 pens together cost Rs 50, whereas 7 pencils and 5 pens together cost Rs 46. Find the cost of one pencil and a pen.
(iii) Champa went to a ‘sale’ to purchase some pants and skirts. When her friends asked her how many of each she had bought, she answered, “The number of skirts is two less than twice the number of pants purchased. Also, the number of skirts is four less than four times the number of pants purchased.” Help her friends to find how many pants and skirts Champa bought.
Sol:
(i) Let the number of girls and boys in the class be x and y respectively.
According to the given conditions, we have:
x + y = 10
x - y = 4
x + y = 10 ⇒ x = 10 - y
Three solutions of this equation can be written in a table as follows: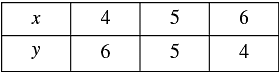
x - y = 4 ⇒ x = 4 + y
Three solutions of this equation can be written in a table as follows: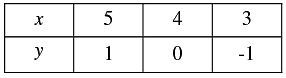
The graphical representation is as follows: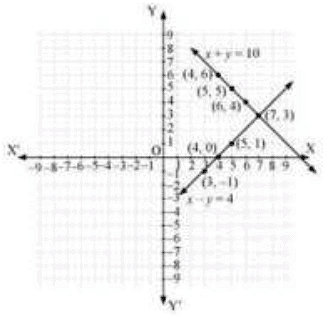
From the graph, it can be observed that the two lines intersect each other at the point (7,3). So. x = 7 and y = 3.
Thus, the number of girls and boys in the class are 7 and 3 respectively.
(ii) Let the cost of one pencil and one pen be Rs x and Rs y respectively.
According to the given conditions, we have:
5x + 7 y = 50
7 x + 5 y = 46
5x + 7 y = 50 ⇒ x = 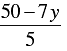
Three solutions of this equation can be written in a table as follows: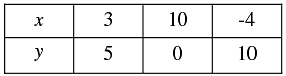
7 x + 5 y = 46 ⇒ x = 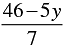
Three solutions of this equation can be written in a table as follows: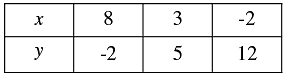
The graphical representation is as follows: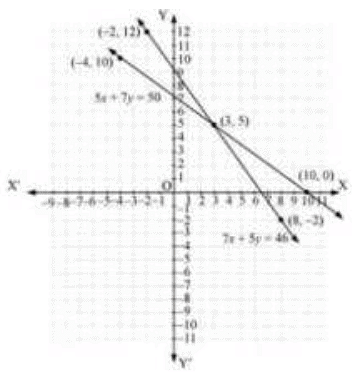
From the graph. It can be observed that the two lines intersect each other at the point (3,5). So. x = 3 and y = 5.
Therefore, the cost of one pencil and one pen are Rs 3 and Rs 5 respectively.
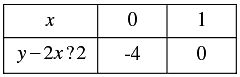
(iii) Let us denote the number of pants by x and the number of skirts by y. Then the equations formed are:
y = 2 x ?2 .....(1) and y = 4 x ?4 .....( 2)
Let us draw the graphs of Equations (1) and (2) by finding two solutions for each of the equations.
linear equations, i.e, th They are given in Table
They are giving table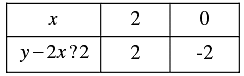
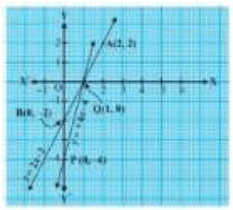
Plot the point and draw the lines passing through them to represent the equation, as shown in fig.
The t lines intersect at the point (10) .So. x -1, y = 0is the required solution of the pair of linear equations, i.e, the number of pants she purchased island she did not buy any skirt Concept insight: Read the question carefully and examine what are the unknowns. Represent the given conditions with the help of equations by taking the unknowns quantities as variables. Also carefully state the variables as whole solution is based on it on the graph paper, mark the points accurately and neatly using a sharp pencil. Also take at least three points satisfying the two equations in order to obtain the correct straight line of the equation. Since joining any two points gives a straight line and if one of the points is computed incorrect will give a wrong line and taking third point will give a correct line. The point where the two straight lines will intersect will give the values of the two variables, i.e., the solution of the two linear equations. State the solution point.
Q.35. Solve the following system of equations graphically: Shade the region between the lines and the y-axis
(i) 3x - 4 y = 7
5x + 2 y = 3
(ii) 4 x - y = 4
3x + 2 y = 14
Sol:
The given system of equations is
3x - 4 y = 7
5x + 2 y = 3
Now,
3x - 4 y = 7
⇒ 3x - 7 = 4 y
⇒ 4 y = 3x - 7
⇒ 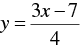
When x = 1, we have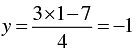
When x = -3, we have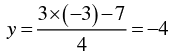
Thus, we have the following table:
We have,
5 x + 2 y = 3
⇒ 2y = 3 - 5x
⇒ 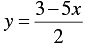
When x = 1, we have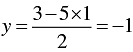
When x = 3, we have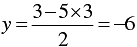
Thus, we have the following table:
Graph of the given system of equations: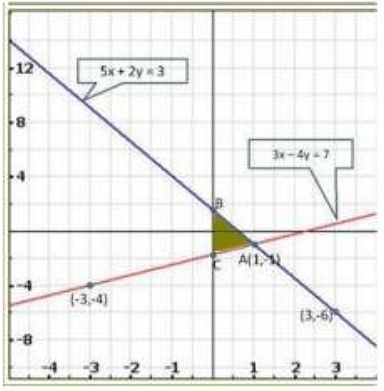
Clearly, the two lines intersect at A (1, -1) Hence, x = 1, y = —1 is the solution of the given system of equations.
We also observe that the required shaded region is ΔABC
The given system of equations is
4 x - y = 4
3x + 2 y = 14
Now,
4 x - y = 4
⇒ 4 x - 4 = y
⇒ y = 4 x - 4
When x = 0, we have
y = 4 X 0 - 4 = -4
When x = -1,we have
y = 4 x(-1)-4 = -8
Thus, we have the following table: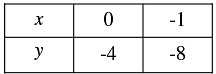
We have,
3x + 2 y = 14
⇒ 2 y = 14 - 3x
⇒ 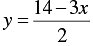
When x = 0, we have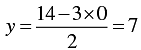
When x = 0, we have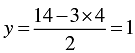
Thus, we have the following table:
Graph of the given system of equations: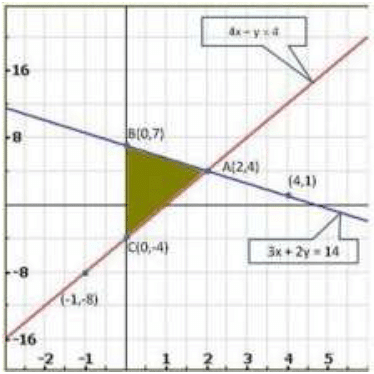
Clearly, the two lines intersect at A(2,4).Hence, x = 2, y = 4 is the solution of the given system of equations.
We also observe ΔABC is the required shaded region.
Q.36. Represent the following pair of equations graphically and write the coordinates of points where the lines intersects y-axis
x + 3 y = 6
2 x - 3 y = 12
Sol:
The given system of equations is
x + 3 y = 6
2 x - 3 y = 12
Now,
x + 3 y = 6
⇒ 3 y = 6 - x
⇒ 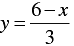
When x = 0, we have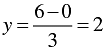
When x = 3, we have
Thus, we have the following table:
We have,
2 x + 3 y = 12
⇒ 2 x -12 - 3x
⇒ 3y = 2x-12
⇒ 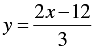
When x = 0, we have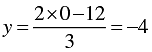
When x = 6, we have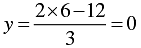
Thus, we have the following table:
Graph of the given system of equations: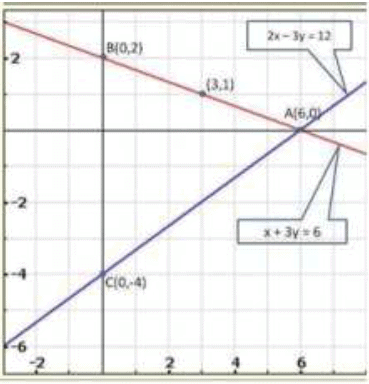
We observe that the lines represented by the equations x + 3y - 6 and 2x - 3y-12 meet y-axis at B (0,2) and C (0, -4) respectively.
Hence, the required co-ordinates are (0,2) and (0, -4).
Q.37. Given the linear equation 2x + 3y - 8 = 0, write another linear equation in two variables such that the geometrical representation of the pair so formed is (i) intersecting lines (ii) Parallel lines (iii) coincident lines
Sol:
(i) For the two lines a1 x + b1 x + c1 = 0 and a2 x + b2 x + c2 = 0, to be intersecting, we must have 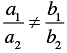
So, the other linear equation can be 5x + 6 y -16 = 0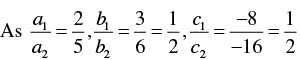
(ii) For the two lines a1x + b1x + c1 = 0 and a2x + b2x + c2 = 0, to be parallel we must have 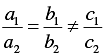
So, the other linear equation can be 6 x + 9y + 24 = 0,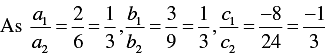
(iii) For the two lines a1x + b1x + c1 = 0 and a2x + b2x + c2 = 0, to be coincident, we must have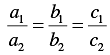
So, the other linear equation can be 6x + 9 y + 24 = 0,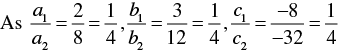
Concept insight: In orders to answer such type of problems, just remember the conditions for two lines to be intersecting parallel, and coincident
This problem will have multiple answers as their can be marry equations satisfying the required conditions.
|
126 videos|457 docs|75 tests
|
FAQs on Pair of Linear Equations in Two Variables - 2 RD Sharma Solutions - Mathematics (Maths) Class 10
| 1. What is the concept of pair of linear equations in two variables? |  |
| 2. How can we solve a pair of linear equations graphically? |  |
| 3. What are the methods used to solve a pair of linear equations algebraically? |  |
| 4. Can a pair of linear equations have no solution? |  |
| 5. Can a pair of linear equations have infinitely many solutions? |  |

|
Explore Courses for Class 10 exam
|

|

















