RS Aggarwal Solutions: Number System- 5 | Extra Documents & Tests for Class 9 PDF Download

Q.1. Represent √5 on the number line.
Ans.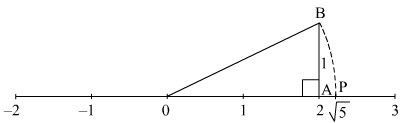

To represent √5 on the number line, follow the following steps of construction:
(i) Mark points 0 and 2 as O and P, respectively.

(ii) At point A, draw AB ⊥ OA such that AB = 1 units.

(iii) Join OB.

(iv) With O as centre and radius OB, draw an arc intersecting the number line at point P.

Thus, point represents √5 on the number line.

Justification:
In right ΔOAB,

Using Pythagoras theorem,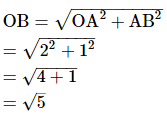


Q.2. Locate √3 on the number line

Ans.

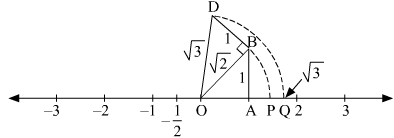
To represent √3 on the number line, follow the following steps of construction:

(i) Mark points 0 and 1 as O and A, respectively.

(ii) At point A, draw AB ⊥ OA such that AB = 1 units.
(iii) Join OB.
(iv) At point B, draw DB ⊥ OA such that DB = 1 units.
(v) Join OD.

(vi) With O as centre and radius OD, draw an arc intersecting the number line at point Q.

Thus, point Q represents √3 on the number line.
Justification:

In right Δ OAB,

Using Pythagoras theorem,

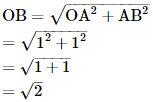
Again, in right ΔODB,
Using Pythagoras theorem,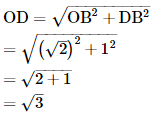


Q.3. Locate √10 on the number line.

Ans.

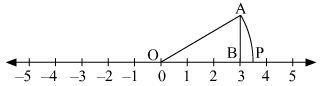
To represent √10 on the number line, follow the following steps of construction:

(i) Mark points 0 and 3 as O and B, respectively.

(ii) At point A, draw AB ⊥ OA such that AB = 1 units.

(iii) Join OA.

(iv) With O as centre and radius OA, draw an arc intersecting the number line at point P.
Thus, point P represents √10 on the number line.

Justification:

In right Δ OAB,
Using Pythagoras theorem,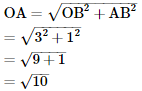


Q.4. Locate √8 on the number line.
Ans.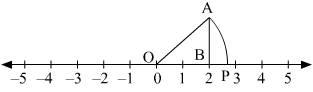

To represent √8 on the number line, follow the following steps of construction:
(i) Mark points 0 and 2 as O and B, respectively.
(ii) At point B, draw AB ⊥ OA such that AB = 2 units.

(iii) Join OA.
(iv) With O as centre and radius OA, draw an arc intersecting the number line at point P.
Thus, point P represents √8 on the number line.
Justification:

In right ΔOAB,
Using Pythagoras theorem,

Q.5. Represent 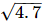 geometrically on the number line.

Ans.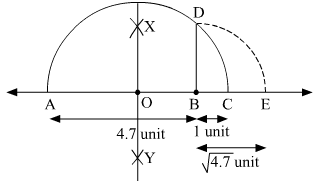

To represent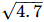on the number line, follow the following steps of construction:
(i) Mark two points A and B on a given line such that AB = 4.7 units.
(ii) From B, mark a point C on the same given line such that BC = 1 unit.

(iii) Find the mid point of AC and mark it as O.
(iv) With O as centre and radius OC, draw a semi-circle touching the given line at points A and C.
(v) At point B, draw a line perpendicular to AC intersecting the semi-circle at point D.
(vi) With B as centre and radius BD, draw an arc intersecting the given line at point E.
Thus, let us treat the given line as the number line, with B as 0, C as 1, and so on, then point E represents .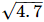
Justification:
Here, in semi-circle, radii OA = OC = OD =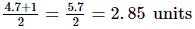
And, OB = AB − AO = 4.7 − 2.85 = 1.85 units
In a right angled triangle OBD,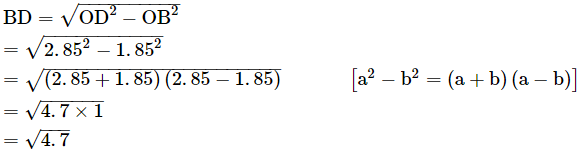


Q.6. Represent 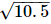 on the number line.
Ans.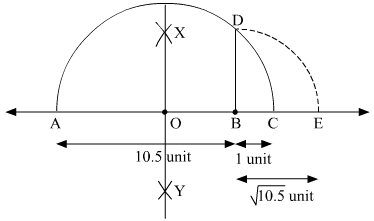

To represent 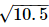 on the number line, follow the following steps of construction:
(i) Mark two points A and B on a given line such that AB = 10.5 units.
(ii) From B, mark a point C on the same given line such that BC = 1 unit.
(iii) Find the mid point of AC and mark it as O.
(iv) With O as centre and radius OC, draw a semi-circle touching the given line at points A and C.
(v) At point B, draw a line perpendicular to AC intersecting the semi-circle at point D.
(vi)  With B as centre and radius BD, draw an arc intersecting the given line at point E.
Thus, let us treat the given line as the number line, with B as 0, C as 1, and so on, then point E represents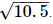
Justification:
Here, in semi-circle, radii OA = OC = OD =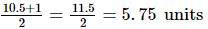
And, OB = AB − AO = 10.5 − 5.75 = 4.75 units
In a right angled triangle OBD,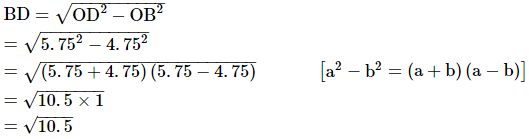


Q.7. Represent 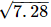 geometrically on the number line.
Ans.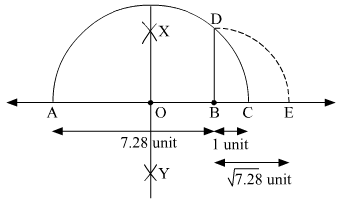

To represent 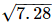 on the number line, follow the following steps of construction:
(i) Mark two points A and B on a given line such that AB = 7.28 units.
(ii) From B, mark a point C on the same given line such that BC = 1 unit.
(iii) Find the mid point of AC and mark it as O.
(iv) With O as centre and radius OC, draw a semi-circle touching the given line at points A and C.
(v) At point B, draw a line perpendicular to AC intersecting the semi-circle at point D.
(vi)  With B as centre and radius BD, draw an arc intersecting the given line at point E.
Thus, let us treat the given line as the number line, with B as 0, C as 1, and so on, then point E represents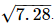
Justification:
Here, in semi-circle, radii OA = OC = OD =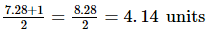
And, OB = AB − AO = 7.28 − 4.14 = 3.14 units
In a right angled triangle OBD,

Q.8. Represent (1 + 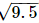) on the number line.
Ans.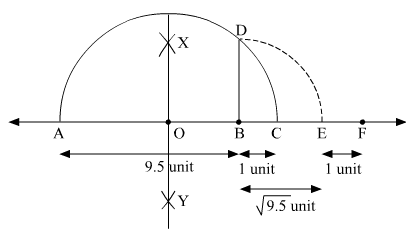

To represent (1 + 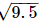) on the number line, follow the following steps of construction:
(i) Mark two points A and B on a given line such that AB = 9.5 units.
(ii) From B, mark a point C on the same given line such that BC = 1 unit.
(iii) Find the mid point of AC and mark it as O.
(iv) With O as centre and radius OC, draw a semi-circle touching the given line at points A and C.
(v) At point B, draw a line perpendicular to AC intersecting the semi-circle at point D.
(vi) With B as centre and radius BD, draw an arc intersecting the given line at point E.
(vii) From E, mark a point F on the same given line such that EF = 1 unit.
Thus, let us treat the given line as the number line, with B as 0, C as 1, E as 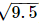 and so on, then point F represents (1+).
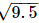Justification:
Here, in semi-circle, radii OA = OC = OD =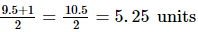
And, OB = AB − AO = 9.5 − 5.25 = 4.25 units
In a right angled triangle OBD,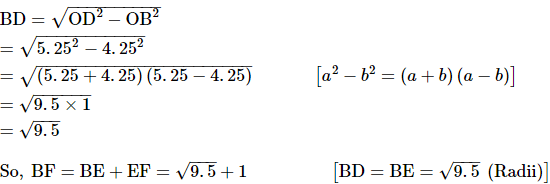


Q.9. Visualize the representation of 3.765 on the number line using successive magnification.
Ans.
3 < 3.765 < 4
Divide the gap between 3 and 4 on the number line into 10 equal parts.
Now, 3.7 < 3.765 < 3.8
In order to locate the point 3.765 on the number line, divide the gap between 3.7 and 3.8
into 10 equal parts.
Further, 3.76 < 3.765 < 3.77
So, to locate the point 3.765 on the number line, again divide the gap between 3.76 and 3.77 into 10 equal parts.

Now, the number 3.765 can be located on the number line. This can be shown as follows: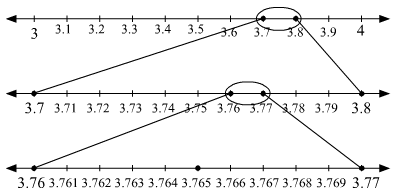

Here, the marked point represents the point 3.765 on the number line.

Q.10. Visualize the representation of 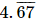 on the number line up to 4 decimal places.
Ans.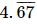
 = 4.6767  (Upto 4 decimal places)

4 < 4.6767 < 5
Divide the gap between 4 and 5 on the number line into 10 equal parts.
Now, 4.6 < 4.6767 < 4.7
In order to locate the point 4.6767 on the number line, divide the gap between 4.6 and 4.7
into 10 equal parts.
Further, 4.67 < 4.6767 < 4.68
To locate the point 4.6767 on the number line, again divide the gap between 4.67 and 4.68 into 10 equal parts.
Again, 4.676 < 4.6767 < 4.677
To locate the point 4.6767 on the number line, again divide the gap between 4.676 and 4.677 into 10 equal parts.
Now, the number 4.6767 can be located on the number line. This can be shown as follows: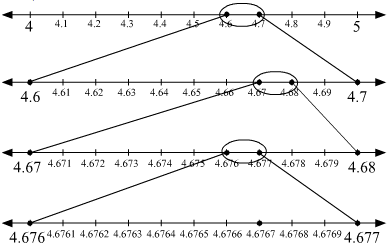

Here, the marked point represents the point 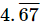 on the number line up to 4 decimal places.