All Courses
Get the App Signup / Login
Sign in Open App
Class 9 Exam  >  Class 9 Notes  >  Extra Documents & Tests for Class 9  >  RS Aggarwal Solutions: Exercise 3G - Factorisation of Polynomials

RS Aggarwal Solutions: Exercise 3G - Factorisation of Polynomials | Extra Documents & Tests for Class 9 PDF Download

Q.1. Find the product: (x + y − z) (x2 + y2 + z2 − xy + yz + zx)
Ans. (x+y−z)(x2+y2+z2−xy+yz+zx)
=[x+y+(−z)][x2+y2+(−z)2−xy−y×(−z)−[−z]×x]
=x3+y3+(−z)3−3x×y×(−z)
=x3+y3−z3+3xyz

Q.2. Find the product: (x – y − z) (x2 + y2 + z2 + xy – yz + xz)
Ans. (x – y − z) (x2 + y2 + z2 + xy – yz + xz)
=(x+(−y)+(−z)) (x2+y2+z2+xy–yz+xz)
We know
(a+b+c)(a2+b2+c2−ab−bc−ca)
=a3+b3+c3−3abc
Here, a=x,b=−y,c=−z
(x+(−y)+(−z)) (x2+y2+z2+xy–yz+xz)
=x3−y3−z3−3xyz

Q.3. Find the product: (x − 2y + 3) (x2 + 4y2 + 2xy − 3x + 6y + 9)
Ans. (x − 2y + 3)(x2+4y2+2xy−3x+6y+9)
=(x − 2y + 3)(x2+4y2+9+2xy+6y−3x)
=[x+(−2y)+3][x2+(−2y)2+(3)2−x×(−2y)−(−2y)×3−3×x]
=(x)3+(−2y)3+(3)3−3(x)(−2y)(3)
=x3−8y3+27+18xy

Q.4. Find the product: (3x – 5y + 4) (9x2 + 25y2 + 15xy − 20y + 12x + 16)
Ans. (3x−5y+4)(9x2+25y2+15xy−20y+12x+16)
=(3x+(−5y)+4)(9x2+25y2+16+15xy−20y+12x)
(a+b+c)(a2+b2+c2−ab−bc−ca)
=a3+b3+c3−3abc
Here, a=3x,b=−5y,c=4
(3x+(−5y)+4)(9x2+25y2+16+15xy−20y+12x)
=(3x)3+(−5y)3+43−3×3x(−5y)(4)
=27x3−125y3+64+180xy

Q.5. Factorize: 125a3 + b3 + 64c3 − 60abc
Ans. 125a3+b3+64c3−60abc=(5a)3+(b)3+(4c)3−3×5a×b×4c
=(5a+b+4c)[(5a)2+(b)2+(4c)2−5a×b−b×4c−5a×4c]
=(5a+b+4c)(25a2+b2+16c2−5ab−4bc−20ac)

Q.6. Factorize: a3 + 8b3 + 64c3 − 24abc
Ans. a3+8b3+64c3−24abc=a3+(2b)3+(4c)3−3×a×2b×4c
=(a+2b+4c)[a2+(2b)2+(4c)2−a×2b−2b×4c−4c×a]
=(a+2b+4c) (a2+4b2+16c2-2ab-8bc-4ca)

Q.7. Factorize: 1 + b3 + 8c3 − 6bc
Ans. 1+b3+8c3−6bc=(1)3+(b)3+(2c)3−3×1×b×2c
=(1+b+2c)[12+b2+(2c)2−1×b−b×2c−1×2c]
=(1+b+2c)(1+b2+4c2−b−2bc−2c)

Q.8. Factorize: 216 + 27b3 + 8c3 − 108abc
Ans. 216+27b3+8c3−108abc
=(6)3+(3b)3+(2c)3−3×6×3b×2c
=(6+3b+2c)[62+(3b)2+(2c)2−6×3b−3b×2c−2c×6]
=(6+3b+2c)(36+9b2+4c2−18b−6bc−12c)

Q.9. Factorize: 27a3 − b3 + 8c3 + 18abc
Ans. 27a3−b3+8c3+18abc=(3a)3+(−b)3+(2c)3−3×(3a)×(−b)×(2c)
=[3a+(−b)+2c][(3a)2+(−b)2+(2c)2−3a(−b)−(−b)2c−3a×2c]
=(3a−b+2c)(9a2+b2+4c2+3ab+2bc−6ac)

Q.10. Factorize: 8a3 + 125b3 − 64c3 + 120abc
Ans. 8a3+125b3−64c3+120abc=(2a)3+(5b)3+(−4c)3−3×(2a)×(5b)×(−4c)
=(2a+5b−4c)[(2a)2+(5b)2+(−4c)2−(2a)(5b)−(5b)(−4c)−(2a)×(−4c)]
=(2a+5b−4c)(4a2+25b2+16c2−10ab+20bc+8ac)

Q.11. Factorize: 8 − 27b3 − 343c3 − 126bc
Ans. 8−27b3−343c3−126bc
=(2)3+(−3b)3+(−7c)3−3×(2)×(−3b)×(−7c)
=[2+(−3b)+(−7c)][(2)2+(−3b)2+(−7c)2−(2)(−3b)−(−3b)(−7c)−(2)(−7c)]
=(2−3b−7c)(4+9b2+49c2+6b−21bc+14c)

Q.12. Factorize: 125 − 8x3 − 27y3 − 90xy
Ans. 125−8x3−27y3−90xy=53+(−2x)3+(−3y)3−3×5×(−2x)×(−3y)
=[5+(−2x) +(−3y)][52+(−2x)2+(−3y)2−5×(−2x)−(−2x)(−3y)−5×(−3y)]                                     =(5−2x−3y)(25+4x2+9y2+10x−6xy+15y)

Q.13. Factorize: 2√2a3 + 16√2b3+c3−12abc
Ans. 2√2a3+16√2b3+c3−12abc
=(√2a)3+(2√2b)3+c3−3×(√2a)×(2√2b)×(c)
=(√2a+2√2b+c)[(√2a)2+(2√2b)2+c2−(√2a)×(2√2b)−(2√2b)×(c)−(2√a)×(c)]
=(√2a+2√2b+c)(2a2+8b2+c2−4ab−2√2bc−√2ac)

Q.14. Factorise: 27x3 – y3 – z3 – 9xyz
Ans. 27x3−y3–z3–9xyz
=(3x)3−y3−z3−3×(3x)×(−y)×(−z)
We know,
a3+b3+c3−3abc
=(a+b+c)(a2+b2+c2−ab−bc−ca)
a=3x,b=−y,c=−z
(3x)3−y3−z3−3×(3x)×(−y)×(−z)
=(3x−y−z)(9x2+y2+z2+3xy−yz+3xz)

Q.15. Factorise: 2√2a3+3√3b3+c3−3√6abc
Ans. 2√2a3+3√3b3+c3−3√6abc
=(√2a)3+(√3b)3+c3−3(√2a)(√3b)c
We know
x3+y3+z3−3xyz=(x+y+z)(x2+y2+z2−xy−yz−zx)
x=√2a,y=√3b,z=c
(√2a)3+(√3b)3+c3−3(√2a)(√3b)c
=(√2a+√3b+c)(2a2+3b2+c2−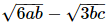RS Aggarwal Solutions: Exercise 3G - Factorisation of Polynomials | Extra Documents & Tests for Class 9 - √2ac)

Q.16. Factorise: 3√3a3−b3−5√5c3−3√15abc
Ans. 3√3a3−b3−5√5c3−3√15abc
=(√3a)3+(−b)3+(−√5c)3−3(√3a)(−b)(−√5c)
We know
x3+y3+z3−3xyz=(x+y+z)(x2+y2+z2−xy−yz−zx)
Here, x=(√3a),y=(−b),z=(−√5c)
3√3a3−b3−5√5c3−3√15abc
=(√3a)3+(−b)3+(−√5c)3−3(√3a)(−b)(−√5c)
=(√3a−b−√5c)(3a2+b2+5c2+√3ab−√5bc+√15c)

Q.17. Factorize: (a − b)3 + (b − c)3 + (c − a)3
Ans. (a−b)3+(b−c)3+(c−a)3
Putting (a−b)=x, (b−c)=y and (c−a)=z, we get:
(a−b)3+(b−c)3+(c−a)3
=x3+y3+z3[Where (x+y+z)=(a−b)+(b−c)+(c−a)=0]
=3xyz [(x+y+z)=0 ⇒x3+y3+z3=3xyz]
=3(a−b)(b−c)(c−a)

Q.18. Factorise: (a−3b)3+(3b−c)3+(c−a)3
Ans. We know x3+y3+z3−3xyz=(x+y+z)(x2+y2+z2−xy−yz−zx)
x3+y3+z3=(x+y+z)(x2+y2+z2−xy−yz−zx)+3xyz
Here, x=(a−3b),y=(3b−c),z=(c−a)
(a−3b)3+(3b−c)3+(c−a)3
=(a−3b+3b−c+c−a)[(a−3b)2+(3b−c)2+(c−a)2−(a−3b)(3b−c)−(3b−c)(c−a)−(c−a)(a−3b)]+3(a−3b)(3b−c)(c−a)
=0+3(a−3b)(3b−c)(c−a)
=3(a−3b)(3b−c)(c−a)

Q.19. Factorize: (3a − 2b)3 + (2b − 5c)3 + (5c − 3a)3
Ans. Put (3a−2b)=x, (2b−5c)=y and (5c−3a)=z.
We have:
x+y+z = 3a−2b+2b−5c+5c−3a=0
Now,(3a−2b)3+(2b−5c)3+(5c−3a)3=x3+y3+z3
=3xyz [Here, x+y+z=0. So, x3 + y3 +z3 = 3xyz]
=3(3a−2b)(2b−5c)(5c−3a)

Q.20. Factorize: (5a − 7b)3 + (9c − 5a)3 + (7b − 9c)3
Ans. Put (5a−7b)=x, (9c−5a)=z and (7b−9c)=y.
Here, x+y+z = 5a − 7b + 9c−5a+7b−9c=0
Thus, we have:
(5a−7b)3+(9c−5a)3+(7b−9c)3=x3+z3+y3
=3xzy   [When x+y+z=0, x3+y3+z3 = 3xyz.]
=3 (5a−7b)(9c−5a)(7b−9c)

Q.21. Factorize: a3(b − c)3 + b3(c − a)3 + c3(a − b)3
Ans. We have: a3(b−c)3+b3(c−a)3+c3(a−b)3 = [a(b−c)]3+[b(c−a)]3+[c(a−b)]3
Put a(b−c) = x
b(c−a) = y
c(a−b) = z
Here, x+y+z = a(b−c)+b(c−a)+c(a−b)
=ab − ac + bc − ab + ac − bc
=0
Thus, we have:
a3(b−c)3+b3(c−a)3+c3(a−b)3 =x3 + y3+ z3
=3xyz [When x+y+z =0, x3 + y3+ z3 =3xyz.]
=3 a(b−c)b(c−a)c(a−b)
=3abc(a−b)(b−c)(c−a)

Q.22. Evaluate
(i) (–12)3 + 73 + 53
(ii) (28)3 + (–15)3 + (–13)3
Ans. (i) (–12)3 + 73 + 53
We know
x3+y3+z3−3xyz=(x+y+z)(x2+y2+z2−xy−yz−zx)
x3+y3+z3=(x+y+z)(x2+y2+z2−xy−yz−zx)+3xyz
Here, x=(−12),y=7,z=5
(−12)3+73+53
=(−12+7+5)[(−12)2+72+52−7(−12)−35+60]+3(−12)×35
=0−1260
= -1260
(ii) (28)3 + (–15)3 + (–13)3
We know
x3+y3+z3−3xyz=(x+y+z)(x2+y2+z2−xy−yz−zx)
x3+y3+z3=(x+y+z)(x2+y2+z2−xy−yz−zx)+3xyz
Here, x=(−28),y=−15,z=−13
(28)3+(−15)3+(−13)3
=(28−15−13)[(28)2+(−15)2+(−13)2−28(−15)−(−15)(−13)−28(−13)]+3×28(−15)(−13)
=0+16380=16380

Q.23. Prove that (a+b+c)3−a3−b3−c3=3(a+b) (b+c) (c+a)
Ans. (a+b+c)3=[(a+b)+c]3
= (a+b)3+c3+3(a+b)c(a+b+c)
⇒(a+b+c)3=a3+b3+3ab(a+b)+c3+3(a+b)c(a+b+c)
⇒(a+b+c)3−a3+b3−c3=3ab(a+b)+3(a+b)c(a+b+c)
⇒(a+b+c)3−a3+b3−c3=3(a+b)[ab+ca+cb+c2]
⇒(a+b+c)3−a3+b3−c3=3(a+b)[a(b+c)+c(b+c)]
⇒(a+b+c)3−a3+b3−c3=3(a+b)(b+c)(a+c)

Q.24. If a, b, c are all nonzero and a + b + c = 0, prove that a2/bc+b2/ca+c2/ab=3.
Ans. a+b+c=0
⇒a3+b3+c3=3abc
Thus, we have:
(a2/bc+b2/ca+c2/ab)=(a3+b3+c3)/abc
=3abc/abc
=3

Q.25. If a + b + c = 9 and a2 + b2 + c2 = 35, find the value of (a3 + b3 + c3 – 3abc).
Ans. a + b + c = 9
⇒(a+b+c)2=92=81
⇒a2+b2+c2+2(ab+bc+ca)=81
⇒35+2(ab+bc+ca)=81
⇒(ab+bc+ca)=23
We know,
(a3 + b3 + c3 – 3abc)
= (a+b+c)(a2+b2+c2−ab−bc−ca)
=(9)(35−23)
=108

The document RS Aggarwal Solutions: Exercise 3G - Factorisation of Polynomials | Extra Documents & Tests for Class 9 is a part of the Class 9 Course Extra Documents & Tests for Class 9.
All you need of Class 9 at this link: Class 9
1 videos|228 docs|21 tests
Join Course for Free

Top Courses for Class 9

Related Exams
About this Document
4.89/5 Rating
Nov 22, 2024 Last updated
Document Description: RS Aggarwal Solutions: Exercise 3G - Factorisation of Polynomials for Class 9 2024 is part of Extra Documents & Tests for Class 9 preparation. The notes and questions for RS Aggarwal Solutions: Exercise 3G - Factorisation of Polynomials have been prepared according to the Class 9 exam syllabus. Information about RS Aggarwal Solutions: Exercise 3G - Factorisation of Polynomials covers topics like and RS Aggarwal Solutions: Exercise 3G - Factorisation of Polynomials Example, for Class 9 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for RS Aggarwal Solutions: Exercise 3G - Factorisation of Polynomials.
Introduction of RS Aggarwal Solutions: Exercise 3G - Factorisation of Polynomials in English is available as part of our Extra Documents & Tests for Class 9 for Class 9 & RS Aggarwal Solutions: Exercise 3G - Factorisation of Polynomials in Hindi for Extra Documents & Tests for Class 9 course. Download more important topics related with notes, lectures and mock test series for Class 9 Exam by signing up for free. Class 9: RS Aggarwal Solutions: Exercise 3G - Factorisation of Polynomials | Extra Documents & Tests for Class 9
Description
Full syllabus notes, lecture & questions for RS Aggarwal Solutions: Exercise 3G - Factorisation of Polynomials | Extra Documents & Tests for Class 9 - Class 9 | Plus excerises question with solution to help you revise complete syllabus for Extra Documents & Tests for Class 9 | Best notes, free PDF download
Information about RS Aggarwal Solutions: Exercise 3G - Factorisation of Polynomials
In this doc you can find the meaning of RS Aggarwal Solutions: Exercise 3G - Factorisation of Polynomials defined & explained in the simplest way possible. Besides explaining types of RS Aggarwal Solutions: Exercise 3G - Factorisation of Polynomials theory, EduRev gives you an ample number of questions to practice RS Aggarwal Solutions: Exercise 3G - Factorisation of Polynomials tests, examples and also practice Class 9 tests
1 videos|228 docs|21 tests
Join Course for Free
Download as PDF
Explore Courses for Class 9 exam

Top Courses for Class 9

Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
10M+ students study on EduRev
Related Searches

ppt

,

Semester Notes

,

pdf

,

RS Aggarwal Solutions: Exercise 3G - Factorisation of Polynomials | Extra Documents & Tests for Class 9

,

RS Aggarwal Solutions: Exercise 3G - Factorisation of Polynomials | Extra Documents & Tests for Class 9

,

Viva Questions

,

Important questions

,

Previous Year Questions with Solutions

,

study material

,

mock tests for examination

,

shortcuts and tricks

,

practice quizzes

,

Extra Questions

,

RS Aggarwal Solutions: Exercise 3G - Factorisation of Polynomials | Extra Documents & Tests for Class 9

,

Free

,

past year papers

,

video lectures

,

Sample Paper

,

Objective type Questions

,

Exam

,

MCQs

,

Summary

;
Additional Information about RS Aggarwal Solutions: Exercise 3G - Factorisation of Polynomials for Class 9 Preparation

RS Aggarwal Solutions: Exercise 3G - Factorisation of Polynomials Free PDF Download

The RS Aggarwal Solutions: Exercise 3G - Factorisation of Polynomials is an invaluable resource that delves deep into the core of the Class 9 exam. These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective. With the help of these notes, you can grasp complex subjects quickly, revise important points easily, and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner, allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material, or toppers' notes, this PDF has got you covered. Download the RS Aggarwal Solutions: Exercise 3G - Factorisation of Polynomials now and kickstart your journey towards success in the Class 9 exam.

Importance of RS Aggarwal Solutions: Exercise 3G - Factorisation of Polynomials

The importance of RS Aggarwal Solutions: Exercise 3G - Factorisation of Polynomials cannot be overstated, especially for Class 9 aspirants. This document holds the key to success in the Class 9 exam. It offers a detailed understanding of the concept, providing invaluable insights into the topic. By knowing the concepts well in advance, students can plan their preparation effectively. Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.

RS Aggarwal Solutions: Exercise 3G - Factorisation of Polynomials Notes

RS Aggarwal Solutions: Exercise 3G - Factorisation of Polynomials Notes offer in-depth insights into the specific topic to help you master it with ease. This comprehensive document covers all aspects related to RS Aggarwal Solutions: Exercise 3G - Factorisation of Polynomials. It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation. Practice papers and question papers enable you to assess your progress effectively. Additionally, the paper analysis provides valuable tips for tackling the exam strategically. Access to Toppers' notes gives you an edge in understanding complex concepts. Whether you're a beginner or aiming for advanced proficiency, RS Aggarwal Solutions: Exercise 3G - Factorisation of Polynomials Notes on EduRev are your ultimate resource for success.

RS Aggarwal Solutions: Exercise 3G - Factorisation of Polynomials Class 9 Questions

The "RS Aggarwal Solutions: Exercise 3G - Factorisation of Polynomials Class 9 Questions" guide is a valuable resource for all aspiring students preparing for the Class 9 exam. It focuses on providing a wide range of practice questions to help students gauge their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation. The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level. Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.

Study RS Aggarwal Solutions: Exercise 3G - Factorisation of Polynomials on the App

Students of Class 9 can study RS Aggarwal Solutions: Exercise 3G - Factorisation of Polynomials alongwith tests & analysis from the EduRev app, which will help them while preparing for their exam. Apart from the RS Aggarwal Solutions: Exercise 3G - Factorisation of Polynomials, students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc. The EduRev App will make your learning easier as you can access it from anywhere you want. The content of RS Aggarwal Solutions: Exercise 3G - Factorisation of Polynomials is prepared as per the latest Class 9 syllabus.
© EduRev
Education Revolution
Follow Us
Signup to see your scores go up
within 7 days!
Takes less than 10 seconds to signup