RD Sharma Solutions (Ex 1.3 to 1.8): Rational Numbers | Mathematics (Maths) Class 8 PDF Download
Exercise 1.3
Q.1. Subtract the first rational number from the second in each of the following:
(i)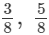
(ii)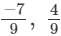
(iii)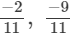
(iv)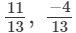
(v)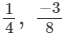
(vi)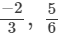
(vii)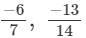
(viii)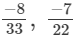
Ans.
(i)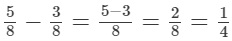
(ii)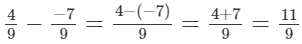
(iii)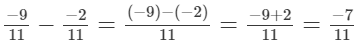
(iv)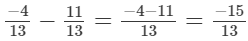
(v)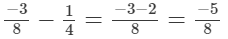
(vi)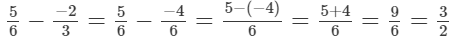
(vii)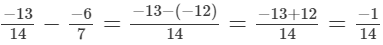
(viii)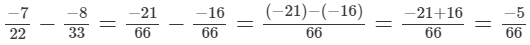
Q.2. Evaluate each of the following:
(i)
(ii)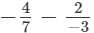
(iii)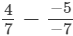
(iv)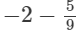
(v)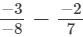
(vi)
(vii)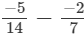
(viii)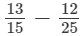
(ix)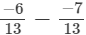
(x)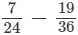
(xi)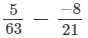
Ans.
(i)
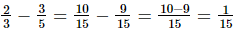
(ii)
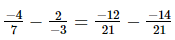 =
=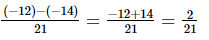
(iii)
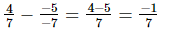
(iv)
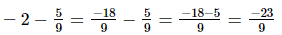
(v)
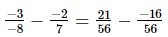 =
=
(vi)
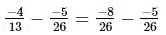 =
=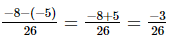
(vii)
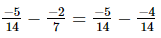 =
=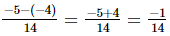
(viii)

(ix)
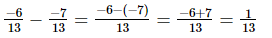
(x)
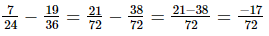
(xi)

Q.3. The sum of the two numbers is 5/9. If one of the numbers is 1/3, find the other.
Ans: It is given that the sum of two numbers is 5/9, where one of the numbers is 1/3.Let the other number be x.

⇒ x =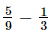
⇒ x =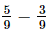
⇒ x =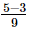
⇒ x =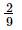
Q.4. The sum of two numbers is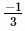 . If one of the numbers is
. If one of the numbers is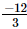 , find the other.
, find the other.
Ans: It is given that the sum of two numbers is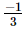 , where one of the numbers is
, where one of the numbers is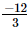 .Let the other number be x.
.Let the other number be x.
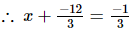
⇒ x =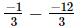
⇒ x =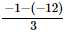 =
= 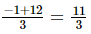
Q.5. The sum of two numbers is −4/3. If one of the numbers is −5, find the other.
Ans: It is given that the sum of two numbers is −4/3, where one of the numbers is −5.Let the other number be x.
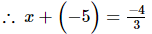
⇒ x =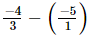
⇒ x =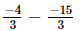
⇒ x =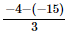
⇒ x =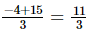
Q.6. The sum of two rational numbers is −8. If one of the numbers is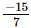 , find the other.
, find the other.
Ans: It is given that the sum of two rational numbers is −8, where one of the numbers is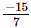 .Let the other rational number be x.
.Let the other rational number be x.
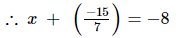
⇒ x =
⇒ x =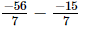
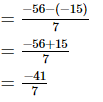
Therefore, the other rational number is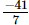 .
.
Q.7. What should be added to −7/8 so as to get 5/9?
Ans: Let x be added to −7/8 so as to get 5/9.
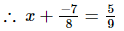
⇒x =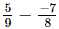
⇒x =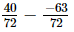
⇒x =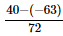
⇒x =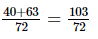
Q.8. What number should be added to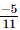 so as to get
so as to get ?
?
Ans:
Let x be added.
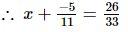
⇒x =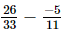
⇒x =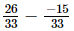
⇒x =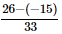
⇒x =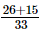
⇒x =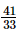
Q.9. What number should be added to −5/7 to get −2/3?
Ans:
Let x be added.
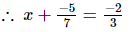
⇒x =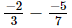
⇒x =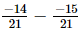
⇒x =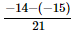
⇒x =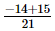
⇒x =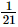
Q.10. What number should be subtracted from −5/3 to get 5/6?
Ans:
Let x be subtracted
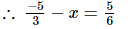
⇒ x =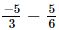
⇒ x =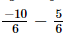
⇒ x =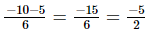
Q.11. What number should be subtracted from 3/7 to get 5/4?
Ans:
Let, x be subtracted.
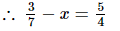
⇒ x =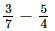
⇒ x =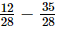
⇒ x =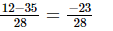
Q.12. What should be added to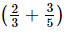 to get
to get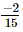 ?
?
Ans:
Let x be added.
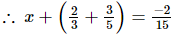
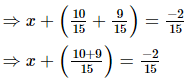
⇒ x =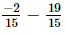
⇒ x =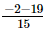
⇒ x =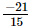
⇒ x =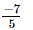
Q.13. What should be added to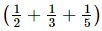 to get 3?
to get 3?
Ans:
Let x be added.
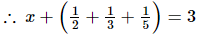
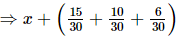 = 3
= 3
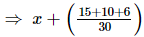 = 3
= 3

⇒ x =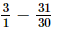
⇒ x =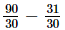
⇒ x =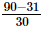
⇒ x =
Q.14. What should be subtracted from to get
to get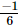 ?
?
Ans:
Let x be subtracted.
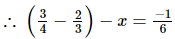
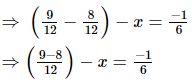
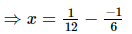
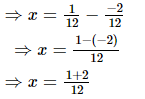
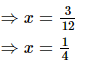
Q.15. Fill in the blanks:
(i)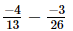 =......
=......
(ii)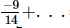 = -1
= -1
(iii)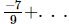 = 3
= 3
(iv)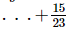 = 4
= 4
Ans:
(i)
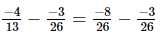 =
= 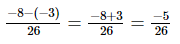
(ii) 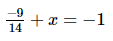
⇒ x =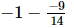
⇒ x =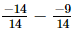
⇒ x =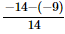
⇒ x =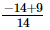
⇒ x =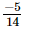
(iii) 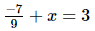
⇒ x =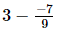
⇒ x =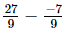
⇒ x =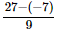
⇒ x =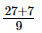
⇒ x =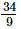
(iv) 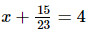
⇒ x =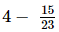
⇒ x =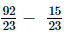
⇒ x =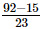
⇒ x =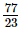
Exercise: 1.4
Q.1. Simplify each of the following and write as a rational number of the form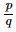 :
:
(i)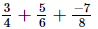
(ii)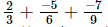
(iii)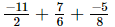
(iv)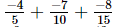
(v)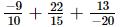
(vi)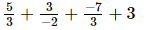
Ans:
(i)
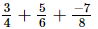
=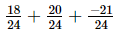
= 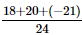
=
(ii)
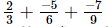
=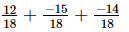
=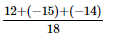
=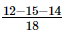
=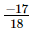
(iii)
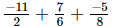
=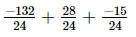
=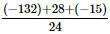
=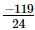
(iv)
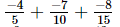
=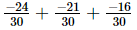
=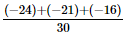
=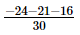
=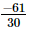
(v)
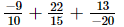
=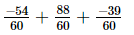
=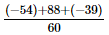
=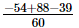
=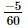
=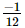
(vi)
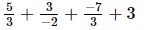
=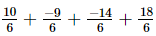
=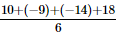
=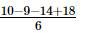
=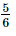
Q.2. Express each of the following as a rational number of the form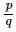 :
:
(i)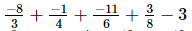
(ii)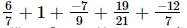
(iii)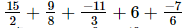
(iv)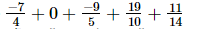
(v)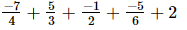
Ans:
(i)
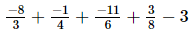
=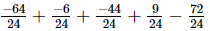
=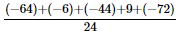
=
=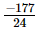
=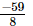
(ii)
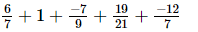
=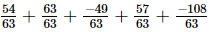
=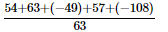
=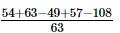
=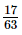
(iii)
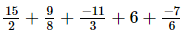
=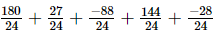
=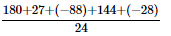
=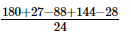
=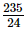
(iv)
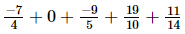
=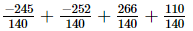
=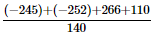
=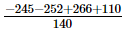
=
(v)
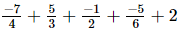
=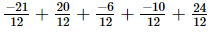
=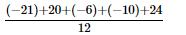
=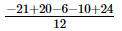
=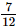
Q.3. Simplify:
(i)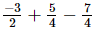
(ii)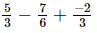
(iii)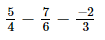
(iv)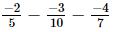
(v)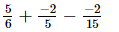
(vi)
Ans:
(i)
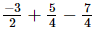
Taking the L.C.M. of the denominators:
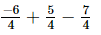
=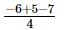
=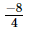
= 2
(ii)

Taking the L.C.M. of the denominators:
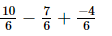
=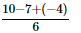
=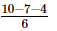
=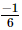
(iii)
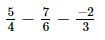
Taking the L.C.M. of the denominators:

=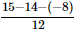
=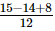
=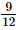
=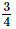
(iv)
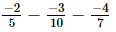
Taking the L.C.M. of the denominators:
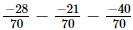
=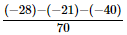
=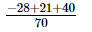
=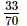
(v)
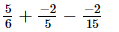
Taking the L.C.M. of the denominators:
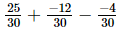
=
=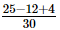
=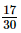
(vi)
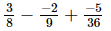
Taking the L.C.M. of the denominators:
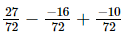
=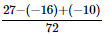
=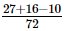
=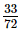
=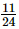
Exercise: 1.5
Q.1. Multiply:
(i)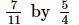
(ii)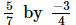
(iii)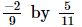
(iv)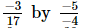
(v)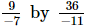
(vi)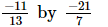
(vii)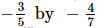
(viii)
Ans:
(i)
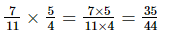
(ii)
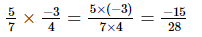
(iii)
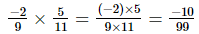
(iv)
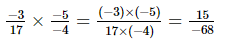
(v)
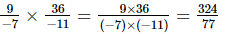
(vi)
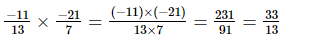
(vii)
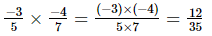
(viii)
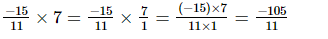
Q.2. Multiply:
(i)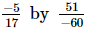
(ii)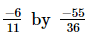
(iii)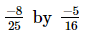
(iv)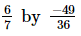
(v)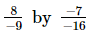
(vi)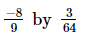
Ans:
(i)
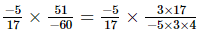 =
= 
(ii)

(iii)
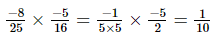
(iv)
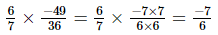
(v)
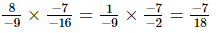
(vi)
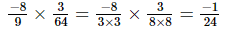
Q.3. Simplify each of the following and express the result as a rational number in standard form:
(i)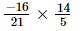
(ii)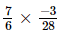
(iii)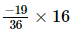
(iv)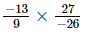
(v)
(vi)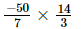
(vii)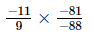
(viii)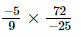
Ans:
(i)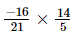 =
= 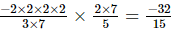
(ii)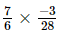 =
= 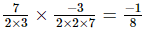
(iii)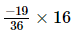 =
= 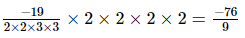
(iv)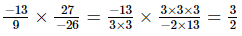
(v)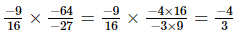
(vi)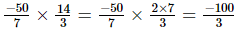
(vii)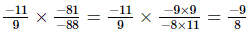
(viii)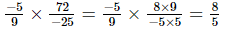
Q.4. Simplify:
(i)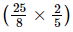 -
- 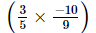
(ii)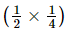 +
+ 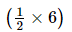
(iii)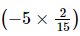 -
- 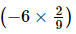
(iv)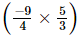 +
+ 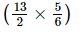
(v)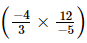 +
+ 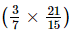
(vi)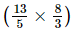 -
- 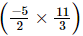
(vii)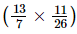 -
- 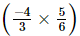
(viii)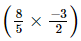 +
+ 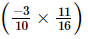
Ans:
(i)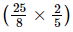 -
- 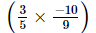
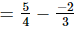
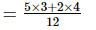
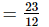
(ii)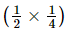 +
+ 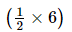
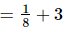
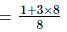
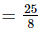
(iii)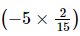 -
- 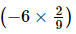
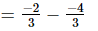


(iv)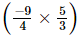 +
+ 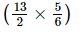
=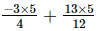
= 
= 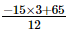
= 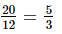
(v)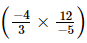 +
+ 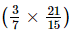
= 
= 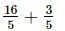
= 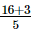
= 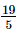
(vi)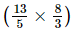 -
- 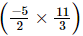
= 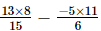
= 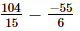
= 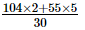
= 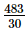
(vii)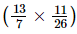 -
- 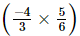
= 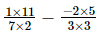
= 
= 
= 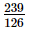
(viii)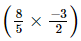 +
+ 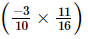
= 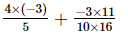
= 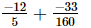
= 
= 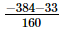
= 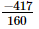
Q.5. Simplify:
(i)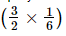 +
+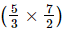 −
−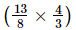
(ii)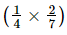 −
−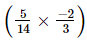 +
+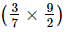
(iii)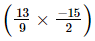 +
+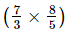 +
+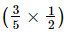
(iv)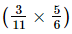 −
−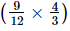 +
+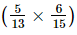
Ans:
(i)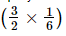 +
+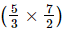 −
−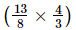
=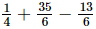
=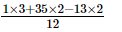
=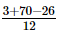
=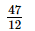
(ii)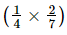 −
−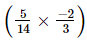 +
+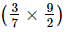
=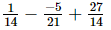
=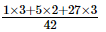
=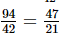
(iii)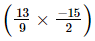 +
+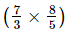 +
+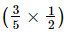
=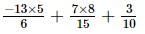
=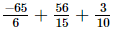
=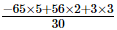
=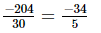
(iv)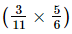 −
−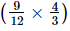 +
+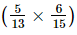
=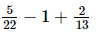
=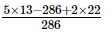
=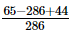
=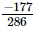
Exercise 1.6
Q.1. Verify the property: x × y = y × x by taking:
(i) x = , y =
, y =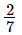
(ii) x =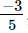 , y =
, y =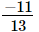
(iii) x =2, y =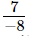
(iv) x =0, y =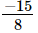
Ans: We have to verify that x × y = y × x.
(i) x = , y =
, y =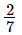
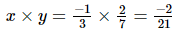
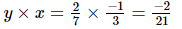
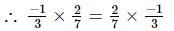
Hence verified.
(ii) x =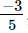 , y =
, y =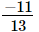
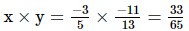
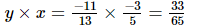
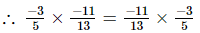
Hence verified.
(iii) x =2, y =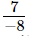
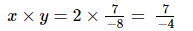
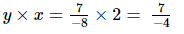
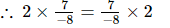
Hence verified.
(iv) x =0, y =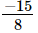
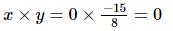
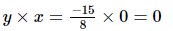
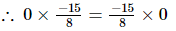
Hence verified.
Q.2. Verify the property: x × (y × z) = (x × y) × z by taking:
(i) x =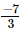 , y =
, y =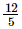 , z =
, z =
(ii) x =0, y = , z =
, z =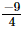
(iii) x = , y =
, y =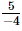 , z =
, z =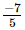
(iv) x =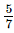 , y =
, y =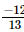 , z =
, z =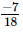
Ans: We have to verify that x × (y × z)=(x × y) × z.
(i) x =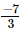 , y =
, y =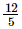 , z =
, z =
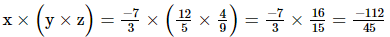
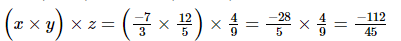
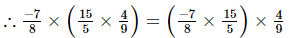
Hence verified.
(ii) x =0, y = , z =
, z =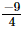
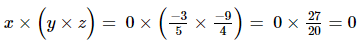
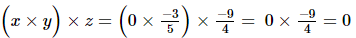
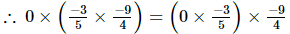
Hence verified.
(iii) x = , y =
, y =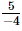 , z =
, z =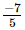
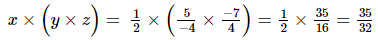
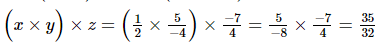
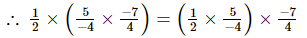
Hence verified.
(iv) x =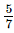 , y =
, y =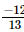 , z =
, z =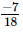
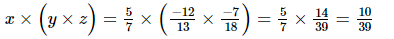
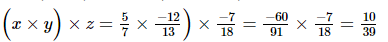
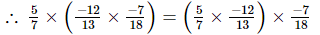
Hence verified.
Q.3. Verify the property: x × (y + z) = x × y + x × z by taking:
(i) x =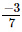 , y=
, y=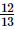 , z=
, z=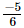
(ii) x =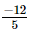 , y=
, y=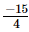 , z=
, z=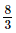
(iii) x =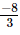 , y=
, y=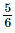 , z=
, z=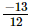
(iv) x =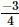 , y=
, y=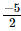 , z=
, z=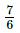
Ans: We have to verify that x × (y + z) = x × y + x × z.
(i) x =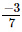 , y=
, y=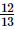 , z=
, z=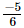
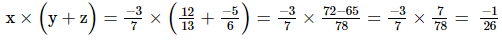
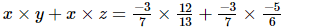
=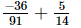
=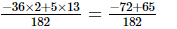
=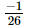
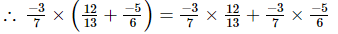
Hence verified.
(ii) x =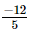 , y=
, y=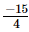 , z=
, z=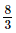
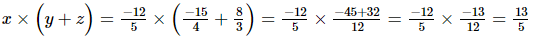
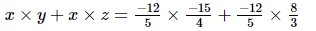
=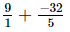
=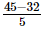
=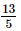
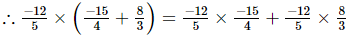
Hence verified.
(iii) x =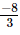 , y=
, y=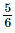 , z=
, z=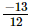
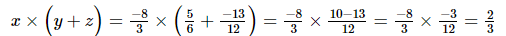
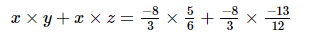
=
=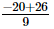
=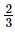
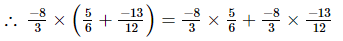
Hence verified.
(iv) x =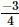 , y=
, y=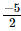 , z=
, z=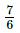
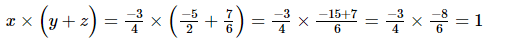
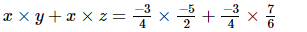
=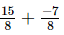
=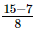
= 1
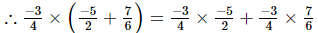
Hence verified.
Q.4. Use the distributivity of multiplication of rational numbers over their addition to simplify:
(i)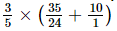
(ii)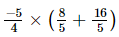
(iii)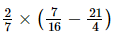
(iv)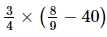
Ans:
(i)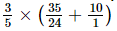 =
=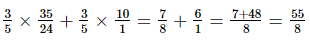
(ii)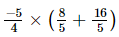 =
= 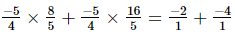 = -6
= -6
(iii)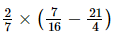 =
= 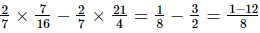 =
= 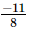
(iv)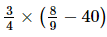 =
= 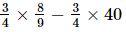 =
=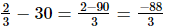
Q.5. Find the multiplicative inverse (reciprocal) of each of the following rational numbers:
(i) 9
(ii) -7
(iii)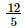
(iv)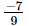
(v)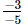
(vi)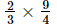
(vii) 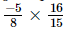
(viii)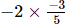
(ix) - 1
(x) 0/3
(xi) 1
Ans:
(i) Multiplicative inverse (reciprocal) of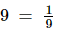
(ii) Multiplicative inverse (reciprocal) of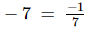
(iii) Multiplicative inverse (reciprocal) of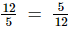
(iv) Multiplicative inverse (reciprocal) of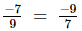
(v) Multiplicative inverse (reciprocal) of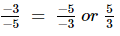
(vi) Multiplicative inverse (reciprocal) of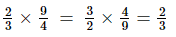
(vii) Multiplicative inverse (reciprocal) of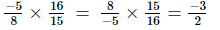
(viii) Multiplicative inverse (reciprocal) of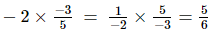
(ix) Multiplicative inverse (reciprocal) of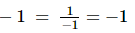
(x) Multiplicative inverse (reciprocal) of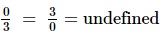
(xi) Multiplicative inverse (reciprocal) of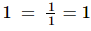
Q.6. Name the property of multiplication of rational numbers illustrated by the following statements:
(i)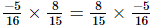
(ii)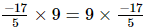
(iii)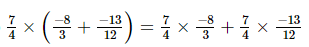
(iv)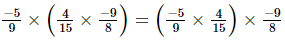
(v)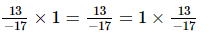
(vi)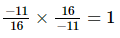
(vii)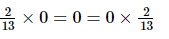
(viii)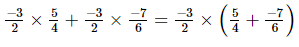
Ans:
(i) Commutative property
(ii) Commutative property
(iii) Distributivity of multiplication over addition
(iv) Associativity of multiplication
(v) Existence of identity for multiplication
(vi) Existence of multiplicative inverse
(vii) Multiplication by 0
(viii) Distributive property
Q.7. Fill in the blanks:
(i) The product of two positive rational numbers is always .....
(ii) The product of a positive rational number and a negative rational number is always .....
(iii) The product of two negative rational numbers is always .....
(iv) The reciprocal of a positive rational number is .....
(v) The reciprocal of a negative rational number is .....
(vi) Zero has ..... reciprocal.
(vii) The product of a rational number and its reciprocal is .....
(viii) The numbers ..... and ..... are their own reciprocals.
(ix) If a is reciprocal of b, then the reciprocal of b is .....
(x) The number 0 is ..... the reciprocal of any number.
(xi) Reciprocal of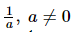 is .....
is .....
(xii) (17 × 12)−1 = 17−1 × .....
Ans:
(i) Positive
(ii) Negative
(iii) Positive
(iv) Positive
(v) Negative
(vi) No
(vii) 1
(viii) -1 and 1
(ix) a
(x) not
(xi) a
(xii) 12−1
Q.8. Fill in the blanks:
(i)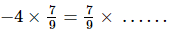
(ii)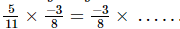
(iii)
(iv)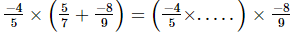
Ans:
(i) −4
x × y = y × x (commutativity)
(ii)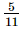
x × y = y × x (commutativity)
(iii)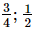
x × (y + z) = x × y + x × z (distributivity of multiplication over addition)
(iv)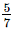
x × (y × z) = (x × y) × z (associativity of multiplication)
Exercise 1.7
Q.1. Divide:
(i)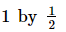
(ii)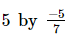
(iii)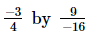
(iv)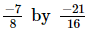
(v)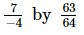
(vi)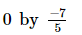
(vii)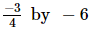
(viii)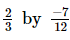
(ix)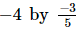
(x)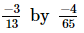
Ans:
(i)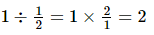
(ii)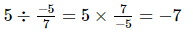
(iii)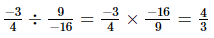
(iv)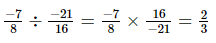
(v)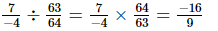
(vi)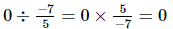
(vii)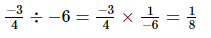
(viii)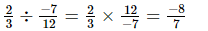
(ix)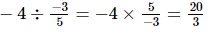
(x)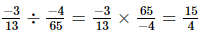
Q.2. Find the value and express as a rational number in standard form:
(i)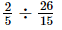
(ii)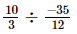
(iii)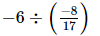
(iv)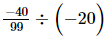
(v)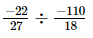
(vi)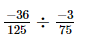
Ans:
(i)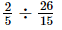 =
=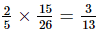
(ii)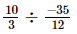 =
=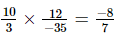
(iii)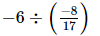 =
=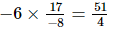
(iv)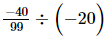 =
=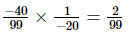
(v)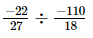 =
=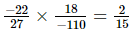
(vi)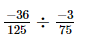 =
=
Q.3. The product of two rational numbers is 15. If one of the numbers is −10, find the other.
Ans: Let the other number be x.
∴ x × (−10) = 15
or x =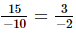
So, the other number is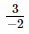 .
.
Q.4. The product of two rational numbers is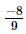 . If one of the numbers is
. If one of the numbers is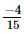 , find the other.
, find the other.
Ans: Let the other number be x.
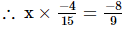
or x =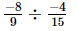
or x =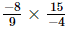
or x =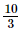
Thus, the other number is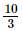 .
.
Q.5. By what number should we multiply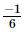 so that the product may be
so that the product may be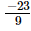 ?
?
Ans: Let the number be x.
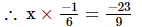
x = 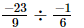
x = 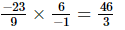
Therefore, the other number is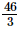 .
.
Q.6. By what number should we multiply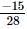 so that the product may be
so that the product may be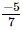 ?
?
Ans: Let the other number be x.
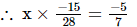
or x =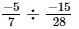
or x =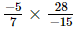
or x =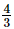
Thus, the other number is 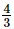 .
.
Q.7. By what number should we multiply so that the product may be 24?
so that the product may be 24?
Ans: Let the number be x.
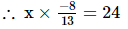
or x =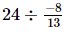
or x =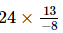
or x = - 39
Thus, the number is −39.
Q.8. By what number should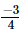 be multiplied in order to produce
be multiplied in order to produce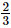 ?
?
Ans: Let the other number that should be multiplied with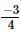 to produce
to produce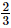 be x.
be x.
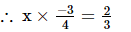
or x =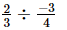
or x =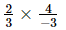
or x =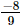
Thus, the number is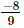 .
.
Q.9. Find (x + y) ÷ (x − y), if
(i) x =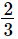 , y =
, y =
(ii) x =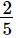 , y =
, y =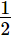
(iii) x =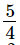 , y =
, y =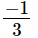
(iv) x =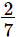 , y =
, y =
(v) x =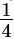 , y =
, y =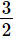
Ans:
(i) x =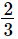 , y =
, y =
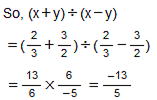
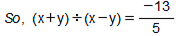
(ii) x =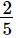 , y =
, y =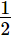
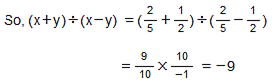
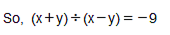
(iii) x =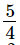 , y =
, y =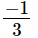
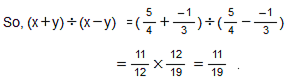

(iv) x =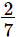 , y =
, y =
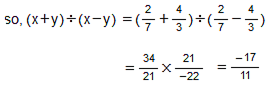
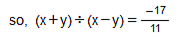
(v) x =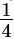 , y =
, y =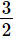
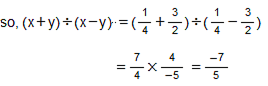
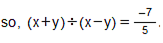
Q.10. The cost of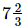 metres of rope is Rs
metres of rope is Rs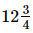 . Find its cost per metre.
. Find its cost per metre.
Ans: The cost of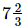 metres of rope is Rs
metres of rope is Rs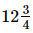 .
.

= 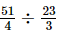
= 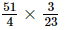
= 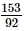
= 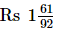
Q.11. The cost of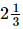 metres of cloth is Rs
metres of cloth is Rs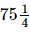 . Find the cost of cloth per metre.
. Find the cost of cloth per metre.
Ans: The cost of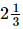 metres of cloth is Rs
metres of cloth is Rs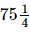 .
.
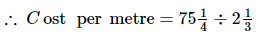
= 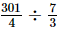
= 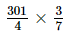
= 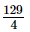
= 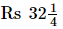
Thus, 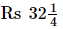 or Rs 32.25 is the cost of cloth per metre.
or Rs 32.25 is the cost of cloth per metre.
Q.12. By what number should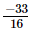 be divided to get
be divided to get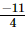 ?
?
Ans: Let the number be x.
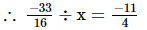
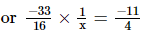
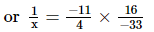
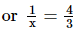
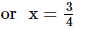
Thus, the number is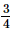 .
.
Q.13. Divide the sum of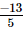 and
and by the product of
by the product of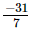 and
and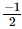 .
.
Ans:
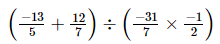
= 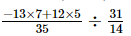
= 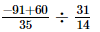
= 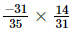
= 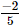
Q.14. Divide the sum of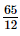 and
and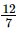 by their difference.
by their difference.
Ans:
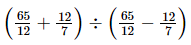
= 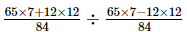
= 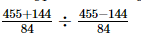
=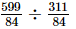
= 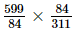
= 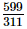
Q.15. If 24 trousers of equal size can be prepared in 54 metres of cloth, what length of cloth is required for each trouser?
Ans: Cloth needed to prepare 24 trousers=54 m
∴ Length of the cloth required for each trousers= 54÷24 = 54/24 = 9/4 m =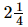 metres.
metres.
Exercise: 1.8
Q.1. Find a rational number between −3 and 1.
Ans: Rational number between −3 and 1 =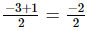 = -1
= -1
Q.2. Find any five rational numbers less than 2.
Ans: We can write:
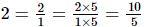
Integers less than 10 are 0, 1, 2, 3, 4, 5 ... 9.
Hence, five rational numbers less than 2 are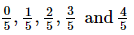 .
.
Q.3. Find two rational numbers between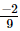 and
and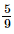 .
.
Ans: Since both the fractions (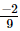 and
and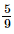 ) have the same denominator, the integers between the numerators(−2 and 5) are −1, 0, 1, 2, 3, 4.Hence, two rational numbers between
) have the same denominator, the integers between the numerators(−2 and 5) are −1, 0, 1, 2, 3, 4.Hence, two rational numbers between 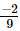 and
and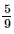 are 0/9 or 0 and 1/9.
are 0/9 or 0 and 1/9.
Q.4. Find two rational numbers between 1/5 and 1/2.
Ans:
Rational number between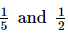 =
= 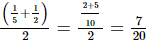
Rational number between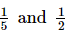 =
= 
Therefore, two rational numbers between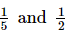 are
are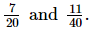
Q.5. Find ten rational numbers between 1/4 and 1/2.
Ans: The L.C.M of the denominators (2 and 4) is 4.
So, we can write 1/4 as it is.
Also, 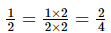
As the integers between the numerators 1 and 2 of both the fractions are not sufficient, we will multiply the fractions by 20.
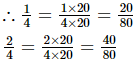
Between 20 and 40, there are 19 integers. They are 21, 22, 23, 24, 25, 26, 27....39, 40.
Thus,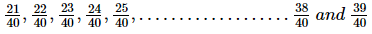 are the fractions.We can take any 10 of these.
are the fractions.We can take any 10 of these.
Q.6. Find ten rational numbers between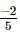 and
and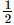 .
.
Ans: L.C.M of the denominators (2 and 5) is 10.
We can write,
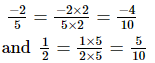
Since the integers between the numerators (−4 and 5 ) of both the fractions are not sufficient, we will multiply the fractions by 2.
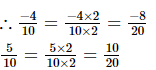
There are 17 integers between −8 and 10, which are −7,−6,−5,−4...................8, 9.These can be written as:
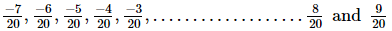
We can take any 10 of these.
Q.7. Find ten rational numbers between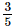 and
and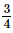 .
.
Ans: The L.C.M of the denominators 5 and 4 of both the fractions is 20.
We can write:
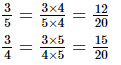
Since the integers between the numerators 12 and 15 are not sufficient, we will multiply both the fractions by 5.
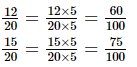
There are 14 integers between 60 and 75. They are 61, 62, 63.......73 and 74.
Therefore, are the 14 fractions.
are the 14 fractions.
We can take any 10 of these.
|
81 videos|423 docs|31 tests
|
FAQs on RD Sharma Solutions (Ex 1.3 to 1.8): Rational Numbers - Mathematics (Maths) Class 8
| 1. How do I find the sum of rational numbers? |  |
| 2. How can I simplify a rational number? |  |
| 3. Can a rational number have a decimal representation? |  |
| 4. How can I convert a decimal number to a rational number? |  |
| 5. Can a rational number be negative? |  |

















