RS Aggarwal Solutions: Exercise 3E - Squares and Square Roots | Mathematics (Maths) Class 8 PDF Download
Q.1. Evaluate: √576
Ans. Using the long division method: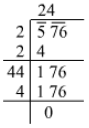
∴ √576 = 24
Q.2. Evaluate: √1444
Ans. Using the long division method: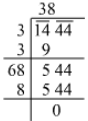
∴ √1444 = 38
Q.3. Evaluate: √4489
Ans. Using the long division method: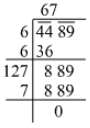
∴ √4489 = 67
Q.4. Evaluate: √6241
Ans. Using the long division method: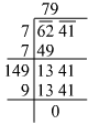
∴ √6241= 79
Q.5. Evaluate: √7056
Ans. Using the long division method: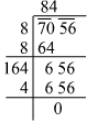
∴ √7056 = 84
Q.6. Evaluate: √9025
Ans. Using the long division method: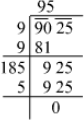
∴ √9025 = 95
Q.7. Evaluate: √11449
Ans. Using the long division method: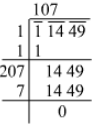
∴ √11449=107
Q.8. Evaluate: √14161
Ans. Using the long division method: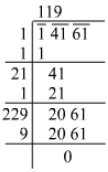
∴ √14161=119
Q.9. Evaluate: √10404
Ans. Using the long division method: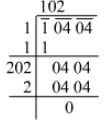
∴ √10404=102
Q.10. Evaluate: √17956
Ans. Using the long division method: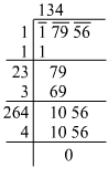
∴ √17956 = 134
Q.11. Evaluate: √19600
Ans. Using the long division method: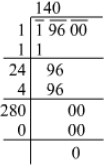
∴ √19600=140
Q.12. Evaluate: √92416
Ans. Using the long division method: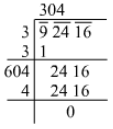
∴ √92416=304
Q.13. Find the least number which must be subtracted from 2509 to make it a perfect square.
Ans. Using the long division method: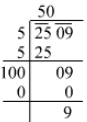
Therefore, the number that should be subtracted from the given number to make it a perfect square is 9.
Q.14. Find the least number which must be subtracted from 7581 to obtain a perfect square. Find this perfect square and its square root.
Ans. Using the long division method: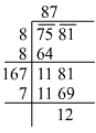
Therefore, the number that should be subtracted from the given number to make it a perfect square is 12.
Perfect square = 7581-12 = 7569
Its square root is 87.
Q.15. Find the least number which must be added to 6203 to obtain a perfect square. Find this perfect square and its square root.
Ans. Using the long division method: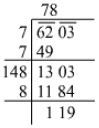
Thus, to get a perfect square greater than the given number, we take the square of the next natural number of the quotient, i.e. 78.
792=6241
Number that should be added to the given number to make it a perfect square =6241−6203=38
The perfect square thus obtained is 6241 and its square root is 79.
Q.16. Find the least number which must be added to 8400 to obtain a perfect square. Find this perfect square and its square root.
Ans. Using the long division method: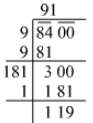
The next natural number that is a perfect square can be obtained by squaring the next natural number of the obtained quotient, i.e. 91.
Therefore square of (91+1) = 922=8464922=8464
Number that should be added to the given number to make it a perfect square =8464−8400=64=8464-8400=64
The perfect square thus obtained is 8464 and its square root is 92.
Q.17. Find the least number of four digits which is a perfect square. Also find the square root of the number so obtained.
Ans. Smallest number of four digits =1000=1000
Using the long division method: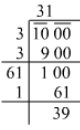
1000 is not a perfect square.
By the long division method, the obtained square root is between 31 and 32.
Squaring the next integer (32) will give us the next perfect square.
322=1024
Thus, 1024 is the smallest four digit perfect square.
Also, √1024=32
Q.18. Find the greatest number of five digits which is a perfect square. Also find the square root of the number so obtained.
Ans. Greatest number of five digits =99999
Using the long division method: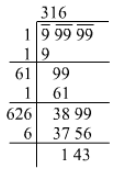
99999 is not a perfect square.
According to the long division method, the obtained square root is between 316 and 317.
Squaring the smaller number, i.e. 316, will give us the perfect square that would be less than 99999.
3162=99856
99856 is the required number.
Its square root is 316.
Q.19. The area of a square field is 60025 m2. A man cycles along its boundary at 18 km/h. In how much time will he return to the starting point?
Ans. Area of the square field = 60025 m2
Length of each side of the square field =√60025=245m
Perimeter of the field =4×245=980 m
= 980/1000 km
The man is cycling at a speed of 18 km/h.
Time = (Distance travelled)/Speed
= (980/1000)/18
= 980/(1000 × 18) hr
= (980 × 60 × 60)/18000 sec
=98 × 2 sec
= 196 sec
= 3 min 16 sec
|
81 videos|423 docs|31 tests
|





















