Exercise 2.2 - Powers RD Sharma Solutions | Mathematics (Maths) Class 8 PDF Download

Q.1. Write each of the following in exponential form:

(i)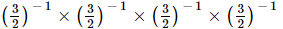

(ii)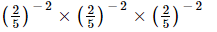

Ans:

(i)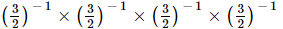= 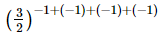{a^m×aⁿ=a^m+n}

=

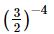
(ii)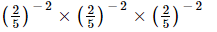= 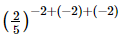{a^m×aⁿ=a^m+n}

=

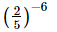
Q.2. Evaluate:

(i) 5⁻²

(ii) (−3)⁻²

(iii) (1/3)⁻⁴

(iv) (−1/2)⁻¹

Ans: 

(i) 5⁻² =

=

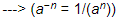
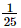
(ii) (−3)⁻² =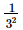

=

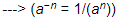
(iii) (1/3)⁻⁴ =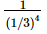

=

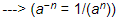
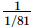
= 81

(iv) (−1/2)⁻¹ =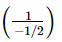

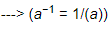
= - 2

Q.3. Express each of the following as a rational number in the form: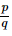

(i) 6⁻¹

(ii) (−7)⁻¹

(iii)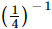

(iv)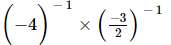

(v)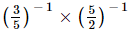

Ans: 

(i) 6⁻¹ =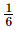

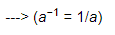
(ii) (−7)⁻¹ =

=

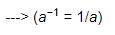
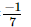
(iii)⁼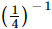

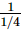
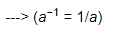
= 4

(iv)=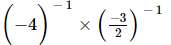  

=

=

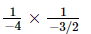
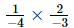
(v) =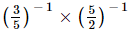  

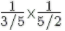
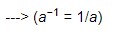
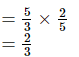
Q.4. Simplify:

(i) {4⁻¹ × 3⁻¹}²

(ii) {5⁻¹ ÷ 6⁻¹}³

(iii) (2⁻¹ + 3⁻¹)⁻¹

(iv) {3⁻¹ × 4⁻¹}⁻¹ × 5⁻¹

(v) (4⁻¹ − 5⁻¹) ÷ 3⁻¹

Ans:

(i) {4⁻¹ × 3⁻¹}² =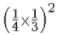

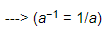
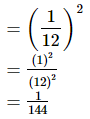
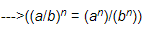
(ii) {5⁻¹ ÷ 6⁻¹}³ =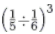

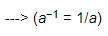
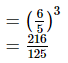
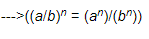
(iii) (2⁻¹ + 3⁻¹)⁻¹ =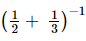

=

=

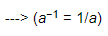
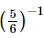
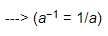
(iv) {3⁻¹ × 4⁻¹}⁻¹ × 5⁻¹ =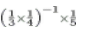

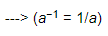
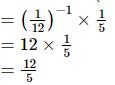
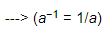
(v) (4⁻¹ − 5⁻¹) ÷ 3⁻¹ =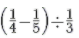

=

=

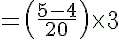
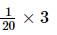
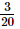
Q.5. Express each of the following rational numbers with a negative exponent:

(i)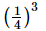

(ii) 3⁵

(iii)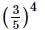

(iv)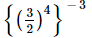

(v)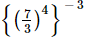

Ans: 

(i)=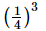 

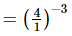
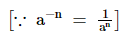
(ii) 3⁵ =  

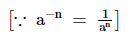
(iii) =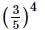  

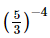
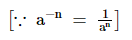
(iv)=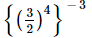

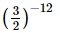
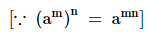
(v)=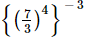  

Q.6. Express each of the following rational numbers with a positive exponent:

(i)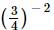

(ii)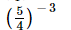

(iii)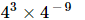

(iv)

(v)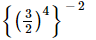

Ans: 

(i)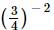

=

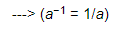
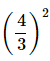
(ii)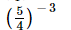 

=

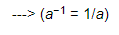
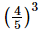
(iii)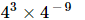

=

=

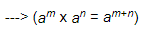
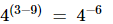
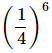
(iv)

=

=

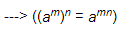
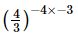
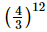
(v)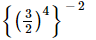

=

=

=

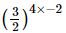
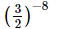
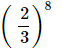
Q.7. Simplify:

(i)

(ii)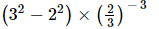

(iii)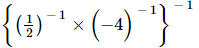

(iv)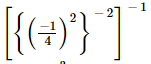

(v)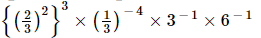

Ans: 

(i) 

=

=

=

=

=

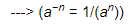
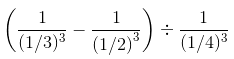
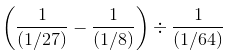
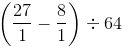
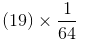
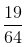
(ii)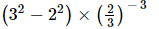

=

=

=

=

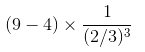
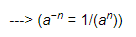
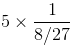
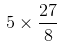
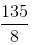
(iii)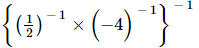

=

=

=

=

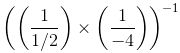
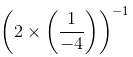
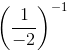
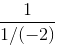
= 2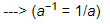

(iv)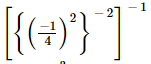

=

=

=

=

=

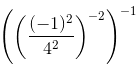
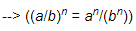
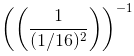
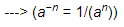
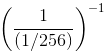
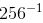
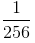
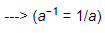
(v)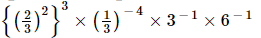

=

=

=

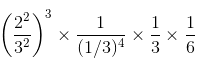
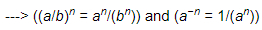
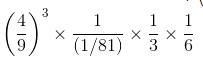
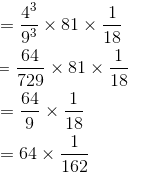
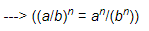
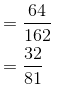
Q.8. By what number should 5⁻¹ be multiplied so that the product may be equal to (−7)⁻¹?

Ans: Expressing in fraction form, we get:

5⁻¹ = 1/5 (using the property a⁻¹ = 1/a)

and

(−7)⁻¹ = −1/7 (using the property a⁻¹ = 1/a).

We have to find a number x such that

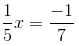
Multiplying both sides by 5, we get:

x=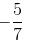

Hence, 5⁻¹ should be multiplied by −5/7 to obtain (−7)⁻¹.

Q.9. By what number should (1/2)⁻¹ be multiplied so that the product may be equal to (−4/7)⁻¹?

Ans: Expressing in fractional form, we get:

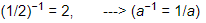
and

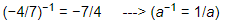
We have to find a number x such that

Dividing both sides by 2, we get:

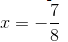
Hence, (1/2)⁻¹ should be multiplied by −7/8 to obtain (−4/7)⁻¹.

Q.10. By what number should (−15)⁻¹ be divided so that the quotient may be equal to (−5)⁻¹?

Ans: Expressing in fractional form, we get:

(−15)⁻¹ = −1/15,      ---> (a⁻¹ = 1/a)

and

(−5)⁻¹ = −1/5           ---> (a⁻¹ = 1/a)

We have to find a number x such that

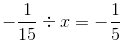
Solving this equation, we get:

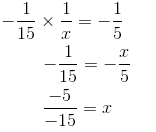
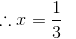
Hence, (−15)⁻¹ should be divided by 1/3 to obtain (−5)⁻¹.

Q.11. By what number should (5/3)⁻² be multiplied so that the product may be (7/3)⁻¹?

Ans: Expressing as a positive exponent, we have:

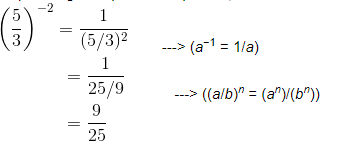
and

(7/3)⁻¹ = 3/7.                ---> (a−¹ = 1/a)

We have to find a number x such that

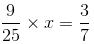
Multiplying both sides by 25/9, we get:

x =

Hence, (5/3⁾⁻² should be multiplied by 25/21 to obtain (7/3)⁻¹.

Q.12. Find x, if

(i)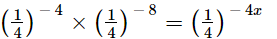

(ii)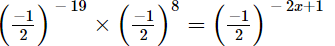

(iii)

(iv)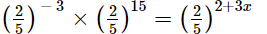

(v)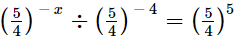

(vi)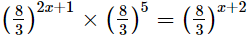

Ans: 

(i) We have:

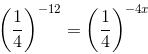(am×an = am(a^m×aⁿ = a^m+n)

-12x = 4

3 = x

x = 3

(ii) We have:

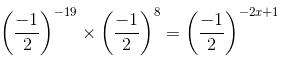
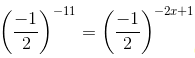(a^m×aⁿ = a^m+n)

-11 = -2x + 1

-12 = -2x

6 = x

x = 6

(iii) We have:

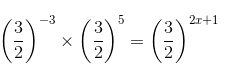
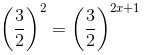
2 = 2x +1

1 = 2x

1/2 = x

x = 1/2

(iv) We have:

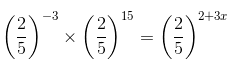
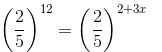
12 = 2 + 3x

10 = 3x

10/3 = x

x = 10 /3

(v) We have:

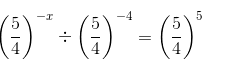
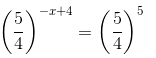
-x + 4 = 5

-x = 1

x = -1

(vi) We have:

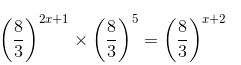
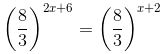
2x +6 = x + 2

x = -4

Q.13. (i) If x =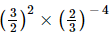, find the value of x⁻².

(ii) If x=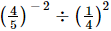, find the value of x⁻¹.

Ans:

(i) First, we have to find x.

x =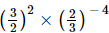  

=

=

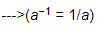
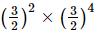
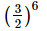
Hence, x⁻² is:

x⁻² =

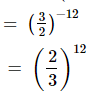
(ii) First, we have to find x.

x =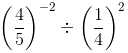

=

=

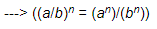
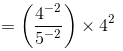
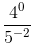
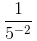
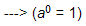
Hence, the value of x⁻¹ is:

x⁻¹ =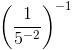

=

=

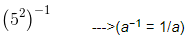
Q.14. Find the value of x for which 5^2x ÷ 5⁻³ = 5⁵.

Ans: We have:

5^2x ÷ 5⁻³ = 5⁵

5^2x+3 = 5⁵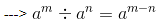

2x + 3 = 5

2x = 2

x = 1

Hence, x is 1.