Exercise 3.9 - Squares And Square Roots RD Sharma Solutions | Mathematics (Maths) Class 8 PDF Download
Q.1. Using square root table, find the square root 7
Ans: From the table, we directly find that the square root of 7 is 2.646.
Q.2. Using square root table, find the square root 15
Ans: Using the table to find √3 and √5
√15 = √3 x √5
= 1.732 × 2.236
= 3.873
Q.3. Using square root table, find the square root 74
Ans: Using the table to find √2 and √37
√74 = √2 x √37
= 1.414 x 6.083
= 8.602
Q.4. Using square root table, find the square root 82
Ans: Using the table to find √2– and √41
√82 = √2 × √41
= 1.414 × 6.403
= 9.055
Q.5. Using square root table, find the square root 198
Ans: Using the table to find √2 and √11
√198 = √2 × √9 × 11
= 1.414 × 3 × 3.317
= 14.070
Q.6. Using square root table, find the square root 540
Ans: Using the table to find √3 and √5
√540 = √54 × √10
=2 × 3√3 × √5
=2 × 3 × 1.732 × 2.2361
=23.24
Q.7. Using square root table, find the square root 8700
Ans: Using the table to find √3 and √29
√8700 = √3 × √29 × √100
= 1.7321 × 5.385 × 10
= 93.27
Q.8. Using square root table, find the square root 3509
Ans: Using the table to find √29
√3509 = √121 × √29
= 11 × 5.3851
= 59.235
Q.9. Using square root table, find the square root 6929
Ans: Using the table to find √41
√6929 = √169 × √41
= 13 × 6.4031
= 83.239
Q.10. Using square root table, find the square root 25725
Ans: Using the table to find √3 and √7
√25725 = √3×5×5×7×7×7
= √3 × 5 × 7 × √ 7
= 1.732 ×5×7×2.646
= 160.41
Q.11. Using square root table, find the square root 1312
Ans: Using the table to find √2 and √41
√1312 = √ 2 × 2 × 2 × 2 × 2 × 41
= 2 × 2√ 2 × √ 41
= 2 × 2 × 1.414 × 6.4031
= 36.222
Q.12. Using square root table, find the square root 4192
Ans:

The square root of 131 is not listed in the table. Hence, we have to apply long division to find it.

Substituting the values:
= 2×2×11.4455 (using the table to find √2)
= 64.75
Q.13. Using square root table, find the square root 4955
Ans: On prime factorisation:
4955 is equal to 5 × 991, which means that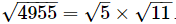
The square root of 991 is not listed in the table; it lists the square roots of all the numbers below 100.
Hence, we have to manipulate the number such that we get the square root of a number less than 100. This can be done in the following manner:
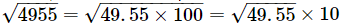
Now, we have to find the square root of 49.55.
We have: 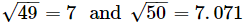
Their difference is 0.071.
Thus, for the difference of 1 (50 − 49), the difference in the values of the square roots is 0.071.
For the difference of 0.55, the difference in the values of the square roots is:
0.55 × 0.0701 = 0.03905
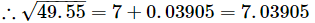
Finally, we have:
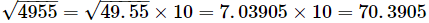
Q.14. Using square root table, find the square root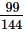
Ans:
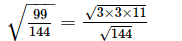
=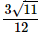
=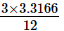 (using the square root table to find √11)
(using the square root table to find √11)
= 0.829
Q.15. Using square root table, find the square root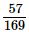
Ans:
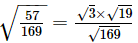
= 

= 0.581
Q.16. Using square root table, find the square root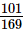
Ans:
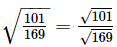
The square root of 101 is not listed in the table. This is because the table lists the square roots of all the numbers below 100.
Hence, we have to manipulate the number such that we get the square root of a number less than 100. This can be done in the following manner:
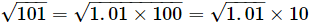
Now, we have to find the square root of 1.01.
We have:
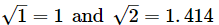
Their difference is 0.414.
Thus, for the difference of 1 (2 − 1), the difference in the values of the square roots is 0.414.
For the difference of 0.01, the difference in the values of the square roots is:
0.01 × 0.414 = 0.00414
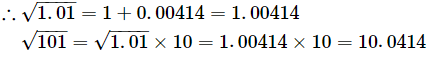
Finally,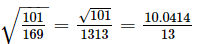 = 0.772
= 0.772
This value is really close to the one from the key answer.
Q.17. Using square root table, find the square root 13.21
Ans: From the square root table, we have:
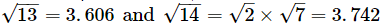
Their difference is 0.136.
Thus, for the difference of 1 (14 − 13), the difference in the values of the square roots is 0.136.
For the difference of 0.21, the difference in the values of their square roots is:
0.136 × 0.21=0.02856
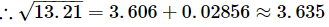
Q.18. Using square root table, find the square root 21.97
Ans: We have to find √21.97
From the square root table, we have:
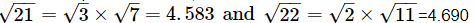
Their difference is 0.107.
Thus, for the difference of 1 (22 − 21), the difference in the values of the square roots is 0.107.
For the difference of 0.97, the difference in the values of their square roots is:
0.107×0.97=0.104
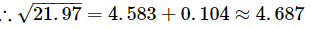
Q.19. Using square root table, find the square root 110
Ans:
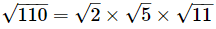
= 1.414 × 2.236 × 3.317 (Using the square root table to find all the square roots) =10.488
Q.20. Using square root table, find the square root 1110
Ans:
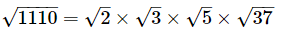
= 1.414 × 1.732 × 2.236 × 6.083 (Using the table to find all the square roots )
= 33.312
Q.21. Using square root table, find the square root 11.11
Ans: We have:
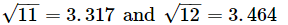
Their difference is 0.1474.
Thus, for the difference of 1 (12 − 11), the difference in the values of the square roots is 0.1474.
For the difference of 0.11, the difference in the values of the square roots is:
0.11 × 0.1474 = 0.0162

Q.22. The area of a square field is 325 m2. Find the approximate length of one side of the field.
Ans: The length of one side of the square field will be the square root of 325.
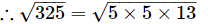
= 5 ×√13
= 5 × 3.605
= 18.030
Hence, the length of one side of the field is 18.030 m.
Q.23. Find the length of a side of a square, whose area is equal to the area of a rectangle with sides 240 m and 70 m.
Ans:
The area of the rectangle = 240 m × 70 m = 16800 m2
Given that the area of the square is equal to the area of the rectangle.
Hence, the area of the square will also be 16800 m2.
The length of one side of a square is the square root of its area.
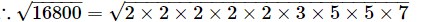
=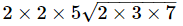
=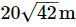
= 129.60 m
Hence, the length of one side of the square is 129.60 m
|
81 videos|423 docs|31 tests
|
















