Math Past Year Paper with Solution - 2020, Class 10 - (Basic) | Mathematics (Maths) Class 10 PDF Download
Class X
Mathematics – Basic
Max. Marks: 80
Duration: 3 hrs.
General Instructions
Read the following instructions very carefully and strictly follow them:
- This question paper comprises four sections – A, B, C and D. This question. Paper carries 40 questions. All questions are compulsory.
- Section A: Question Number 1 to 20 comprises of 20 questions of one mark each.
- Section B: Question Number 21 to 26 comprises of 6 questions of two marks each.
- Section C: Question Number 27 to 34 comprises of 8 questions of three marks each.
- Section D: Question Number 35 to 40 comprises of 6 questions of four marks each.
- There is no overall choice in the question Paper. However, an internal choice has been provided in 2 questions of one mark, 2 questions of two marks, 3 questions of three marks and 3 questions of four marks. You have to attempt only one of the choices in such questions.
- In addition to this, separate instructions are given with each section and question, wherever necessary.
- Use of calculators is not permitted.
Section - A
Question numbers 1 to 20 carry 1 mark each. Choose the correct option in question numbers 1 to 10.
Q.1. If a pair of linear equations is consistent, then the lines represented by them are (1 Mark)
(a) parallel
(b) intersecting or coincident
(c) always coincident
(d) always intersecting
Ans. b
Solution.
intersecting or coincident If a pair of linear equations is consistent, then the lines represented by them are intersecting or coincident.
Q.2. The distance between the points (3, –2) and (–3, 2) is (1 Mark)
(a) √52 units
(b) 4√10 units
(c) 2√10 units
(d) 40 units
Ans. a
Solution.
Distance =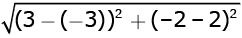
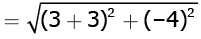
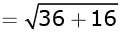
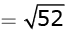
Q.3. 8 cot2A – 8 cosec2 A equal to (1 Mark)
(a) 8
(b) 1/8
(c) -8
(d) -1/8
Ans. c
Solution.
8 cot2A 8 cosec2 A
= 8(cot2 A cosec2 A)
= 8 x -1
= -8
Q.4. The total surface area of a frustum-shaped glass tumbler is (r1 > r2) (1 Mark)
(a) πr1 l + πr2 l
(b) πl (r1 + r2) + πr22
(c) 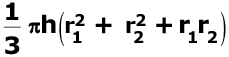
(d) 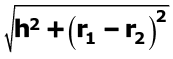
Ans. c
Solution.
The total surface area of a frustum-shaped glass tumbler is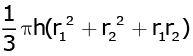 where radii r1 > r2.
where radii r1 > r2.
Q.5. 120 can be expressed as a product of its prime factors as (1 Mark)
(a) 5 x 8 x 3
(b) 15 x 23
(c) 10 x 22 x 3
(d) 5 x 23 x 3
Ans. d
Solution.
120 = 20 × 6
= 5 × 4 × 2 × 3
= 5 × 23 × 3
Q.6. The discriminant of the quadratic equation 4x2 – 6x + 3 = 0 is (1 Mark)
(a) 12
(b) 84
(c) 2√3
(d) –12
Ans. d
Solution.
The given equation is:
4x2 – 6x + 3 = 0
Discriminant = b2 – 4ac
Here, b = –6, a = 4, and c = 3
So, Discriminant = (–6)2 – 4 × 4 × 3
= 36 – 48 = –12
Q.7. If (3, – 6) is the mid-point of the line segment joining (0, 0) and (x, y), then the point (x, y) is (1 Mark)
(a) (–3, 6)
(b) (6, – 6)
(c) (6, –12)
(d) (3/2, -3)
Ans. c
Solution. (3, –6) is the mid-point of the line segment joining
(0, 0) and (x, y).
So, (0 + x)/2 = 3 or, x = 6
And (0 + y)/2 = –6 or, y = –12
Q.8. In the circle given in Figure-1, the number of tangents parallel to tangent PQ is (1 Mark)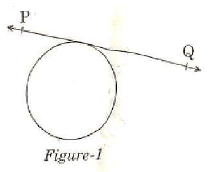 (a) 0
(a) 0
(b) many
(c) 2
(d) 1
Ans. d
Solution.
In the given figure, number of tangents parallel to tangent PQ is 1.
Q.9. For the following frequency distribution: (1 Mark)
The upper limit of median class is
(a) 15
(b) 10
(c) 20
(d) 25
Ans. a
Solution. 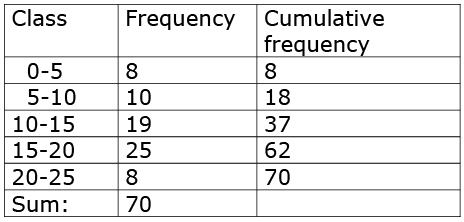
Sum of frequencies (n)= 70
Middle observation = ((n/2) + 1)th observation
= (70/2 + 1)th observation
= 36th observation
36th observation lies in class interval 10 - 15. So, median class is 10 - 15 and its upper limit is 15.
Q.10. The probability of an impossible event is (1 Mark)
(a) 1
(b) 1/2
(c) not defined
(d) 0
Ans. d
Solution.
The probability of an impossible event is 0.
Fill in the blanks in question numbers 11 to 15. (1 Mark)
Q.11. A line intersecting a circle in two points is called a______.
Ans. secant
Q.12. If 2 is a zero of the polynomial ax2 ─ 2x, then the value of 'a' is _________. (1 Mark)
Ans. a(2)2 - 2 x 2 = 0
⇒ 4a - 4 = 0
⇒ a = 1
Q.13. All squares are________. (congruent/similar) (1 Mark)
Ans. similar
Q.14. If the radii of two spheres are in the ratio 2 : 3, then the ratio of their respective volumes is_______. (1 Mark)
Ans. r1 : r2 = 2 : 3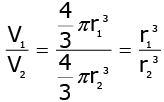
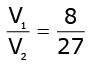
= 8 : 27
Q.15. If ar (ΔPQR) is zero, then the points P, Q and R are_______. (1 Mark)
Ans. collinear
Answer the following question numbers 16 to 20
Q.16. In Figure-2, the angle of elevation of the top of a tower AC from a point B on the ground is 60°. If the height of the tower is 20 m, find the distance of the point from the foot of the tower. (1 Mark)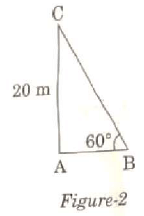 Ans. tan 60° = 20 / AB
Ans. tan 60° = 20 / AB
√3 = 20 / AB
AB = 20 / √3
So, the required distance is 20 / √3 m.
Q.17. Evaluate: tan 40° x tan 50° (1 Mark)
OR
If cos A = sin 42°, then find the value of A. (1 Mark)
Ans. tan40° x tan50°
= tan (90° - 50°) x tan50°
= cot 50° x tan50°
= 1 (∵ tan θ cot θ = 1)
OR
cos A = sin42°
⇒ cos A = sin (90° - 48°)
⇒ cos A = cos 48°
⇒ A = 48°
Q.18. A coin is tossed twice. Find the probability of getting head both the times. (1 Mark)
Ans. All possible outcomes are HH, HT, TT, TH.
Probability of an event = Number of favourable outcomes / Number of all possible outcomes
Probability of getting head both the times = 1 / 4.
Q.19. Find the height of a cone of radius 5 cm and slant height 13 cm. (1 Mark)
Ans.
Height of the cone =

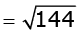
= 12
Therefore, the height of the cone is 12m.
Q.20. Find the value of x so that ─6, x, 8 are in A.P. (1 Mark)
OR
Find the 11th term of the A.P. ─27, ─22, ─17, ─12, …. (1 Mark)
Ans. -6, x, 8 are in A.P.
⇒ 2x = -6 + 8
⇒ 2x = 2
⇒ x = 1
OR
-27, -22, -17, -12,...
an = a + (n - 1)d
a11 = -27 + (11 - 1) x 5
= -27 + 50
= 23
Section - B
Question numbers 21 to 26 carry 2 marks each.
Q.21. Find the roots of the quadratic equation. (2 Marks)
3x2 - 4√3 x + 4 = 0
Ans. 3x2 - 4√3x + 4 = 3x2 - 2√3x - 2√3x + 4
= √3x (√3x - 2) - 2 (√3x - 2)
= (√3x - 2) (√3x - 2)
So, the roots of the equation are the values of x for which
(√3x - 2)(√3x - 2) = 0
Now, √3x - 2 = 0 for x = 2 / √3
So, this root is repeated twice, one for each repeated factor √3x - 2.
Therefore, the roots of 3x2 - 4√3x + 4 are 2 / √3, 2 / √3.
Q.22. Check whether 6n can end with the digit '0' (zero) for any natural number n. (2 Marks)
OR
Find the LCM of 150 and 200. (2 Marks)
Ans. If the number 6n, for any n, were to end with the digit zero, then it would be divisible by 5.
That is, the prime factorisation of 6n would contain the prime 5. This is not possible
∵ 6n = (2 x 3)n
So, the prime numbers in the factorisation of 6n are 2 and 3.
So, the uniqueness of the Fundamental Theorem of Arithmetic guarantees that there are no other primes in the factorisation of 6n.
So, there is no natural number n for which 6n ends with the digit zero.
OR
We have,
150 = 52 x 3 x 2
and, 200 = 52 x 23
Here, 23, 31 and 52 are the greatest powers of the prime factors 2, 3 and 5 respectively involved in the two numbers.
So, LCM(150, 200) = 23 x 31 x 52 = 600.
Q.23. If tan (A + B) = √3 and tan (A - B) = 1 / √3, 0 < A + B 3 ≤ 90°, A > B, then find the values of A and B. (2 Marks)
Ans. We have
tan (A + B) = √3
or tan (A + B) = tan60°
or A + B = 60°......(1)
Again, we have
tan (A - B) = 1 / √3
or tan (A - B) = tan30°
or A - B = 30°....(2)
On adding equations (1) and (2), we get
2A = 90°
or A = 45°
On putting this value of A in equation (1), we get
B = 15°
Q.24. In Figure-3, ΔABC and ΔXYZ are shown. If AB = 3 cm, BC = 6 cm, AC = 2√3 cm, ∠A = 800, ∠B 600, XY = 4√3 cm, YZ = 12 cm and XZ = 6 cm, then find the value of ∠Y. (2 Marks) Ans. In ΔABC and ΔXZY,
Ans. In ΔABC and ΔXZY,
BC / ZY = 6 / 12
= 1 / 2
AC / XY = 2√3 / 4√3
= 1 / 2
AB / XZ = 3 / 6
= 1 / 2
Ratios of the corresponding sides of the given pair of triangles are equal.
i.e., BC / YZ = AC / XY = AB / XZ = 1 / 2.
Therefore, by SSS similarity critarion, ΔABC ~ ΔXZY.
The corresponding angles are equal in ΔABC and ΔXZY. i.e.,
∠A = ∠X = 80°,
∠B = ∠Z = 60°
and
∠C = ∠Y
In ΔABC,
∠A + ∠B + ∠C = 180°
⇒ 80° + 60° + ∠C = 180°
⇒ ∠C = 180° - 140°
⇒ ∠C = 40°
⇒ ∠Y = 40°
Q.25. 14 defective bulbs are accidentally mixed with 98 good ones. It is not possible to just look at the bulb and tell whether it is defective or not. One bulb is taken out at random from this lot. Determine the probability that the bulb taken out is a good one. (2 Marks)
Ans. Number of defective bulbs = 14
Number of good bulbs = 98
Total number of outcomes = 98 +14 = 112
Probability of getting a good bulbs = Number of favourable outcomes / Total number of outcomes
= 98 = 112
= 7 / 8.
Q.26. Find the mean for the following distribution: (2 Marks)
OR
The following distribution shows the transport expenditure of 100 employees: (2 Marks)
Find the mode of the distribution.
Ans.
Here, we observe that class marks and frequencies are small quantities.
So, we use direct method to compute the mean and proceed as below.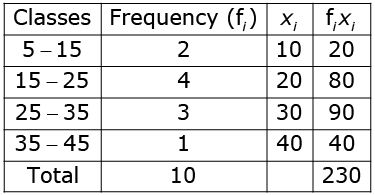
Mean,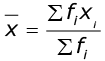
= 230 / 10
= 23
Therefore, mean for the following distribution is 23.
OR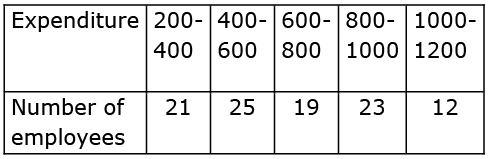
From the given data, we have
l = 400, f1 = 25, f0 = 21, f2 = 19, h = 200
Mode = 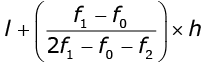

= 480
Mode of the given data is 480.
Section - C
Question number 27 to 34 carry 3 marks each.
Q.27. A quadrilateral ABCD is drawn to circumscribe a circle. Prove that: AB + CD = AD + BC. (3 Marks)
Ans.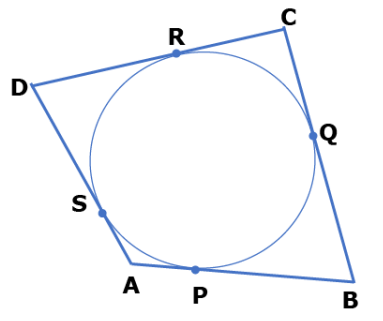 In the given figure, quadrilateral ABCD is circumscribing the given circle and its sides are touching the circle at P, Q, R and S.
In the given figure, quadrilateral ABCD is circumscribing the given circle and its sides are touching the circle at P, Q, R and S.
We have to prove that
AB + CD = AD + BC
We know that lengths of tangents drawn from a point to a circle are equal.
Therefore, from figure, we have
DR = DS, CR = CQ, AS = AP, BP = BQ
Now,
L.H.S. = AB + CD = (AP + BP) + (CR + DR)
= (AS + BQ) + (CQ + DS)
= AS + DS + BQ + CQ
= AD + BC
= R.H.S.
Q.28. The difference between two numbers is 26 and the larger number exceeds thrice of the smaller number by 4. Find the numbers. (3 Marks)
OR
Solve for x and y: (3 Marks)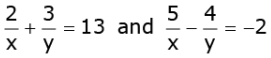
Ans. Let the larger number be y and the smaller number be x.
According to question, y - x = 26......(1)
and y = 3x + 4....(2)
Substituting the value of y from equation (2) in equation (1), we get
3x + 4 - x = 26
or 2x = 26 - 4
or 2x = 22
or x = 11
Putting this value of x in equation (1), we get
y - 11 = 26
or y = 26 + 11 = 37
Hence, the numbers are 11 and 37.
OR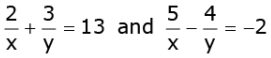
Let 1 / x = p and 1 / y = q
then given equations can be written as:
2p + 3q = 13
2p + 3q - 13 = 0......(1)
and
5p - 4q = -2
5p - 4q + 2 = 0......(2)
Using cross-multiplication method, we get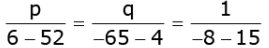
⇒ p / - 46 = q / -69 = 1 / -23
⇒ p / - 46 = 1 / -23 and q / - 69 = 1 / -23
⇒ p = -46 / -23 and q = -69 / -23
⇒ p = 2 and q = 3
⇒ 1 / x = 2 and 1 / y = 3
⇒ x = 1 / 2 and y = 1 / 3
Q.29. Prove that √3 is an irrational number. (3 Marks)
Ans. Let us assume that √3 is rational.
So we can find integers r and s(≠ 0) such that √3 = r / s.
Suppose r and s have a common factor other than 1.
Then we divide r and s by the common factor and get
√3 = a / b
where a and b are coprime.
So, √3b = a
Squaring on both sides, we get
3b2 - a2
Therefore,
a2 is divisible by 3, and so a is also divisible by 3.
So, we can write a = 3c for some integer c.
Now,
3b2 = a2
⇒ 3b2 = 9c2
⇒ b2 = 3c2.
This means that b2 is divisible by 3, and so b is also divisible by 3.
Therefore,
a and b have at least 3 as a common factor.
But this contradicts the fact that a and b are coprime.
So, our assumption that √3 is a rational is wrong.
Hence, √3 is an irrational number.
Q.30. Krishna has an apple orchard which has a 10 m × 10 m sized kitchen garden attached to it. She divides it into a 10 × 10 grid and puts soil and manure into it. She grows a lemon plant at A, a coriander plant at B, an onion plant at C and a tomato plant at D. Her husband Ram praised her kitchen garden and points out that on joining A, B, C and D they may form a parallelogram. Look at the below figure carefully and answer the following questions: (3 Marks)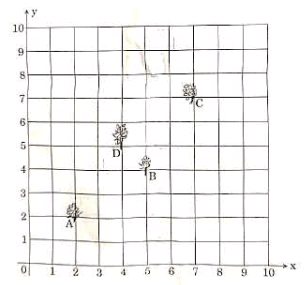 (i) Write the coordinates of the points A, B, C and D, using the 10 × 10 grid as coordinate axes.
(i) Write the coordinates of the points A, B, C and D, using the 10 × 10 grid as coordinate axes.
(ii) Find whether ABCD is a parallelogram or not.
Ans. (i) From the given figure, the coordinates of points A, B, C and D can be written as below: A(2, 2), B(5, 4), C(7, 7) and D(4, 5).
(ii) We know that a quadrilateral is a parallelogram if its opposite sides are equal.
Now, using distance formula, we will find the length of each side of the quadrilateral ABCD.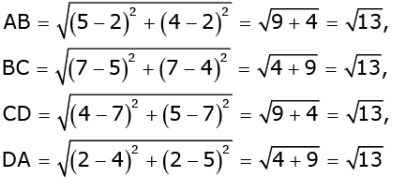
We see that sides AB, BC, CD and DA are equal in lengths, Therefore, quadrilateral ABCD is a parallelogram.
Q.31. If the sum of the first 14 terms of an A.P. is 1050 and its first term is 10, then find the 21st term of the A.P. (3 Marks)
Ans. Here, S14 = 1050, a = 10
We have to find a21.
We know that sum of first n terms of an AP is given by
S = n / 2 [2a + n - 1 d]
So,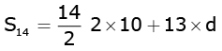
1050 = 7(20 + 13d)
or d = 10
We know that
an = a + (n - 1)d
So, a21 = 10+ (21 - 1)10
= 10 + 20 x 10
= 210.
Q.32. Construct a triangle with its sides 4 cm, 5 cm and 6 cm. Then construct a triangle similar to it whose sides are 2/3 of the corresponding sides of the first triangle. (3 Marks)
OR
Draw a circle of radius 2.5 cm. Take a point P at a distance of 8 cm from its centre. Construct a pair of tangents from the point P to the circle. (3 Marks)
Ans. 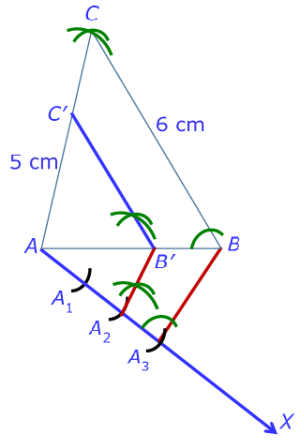 Step 1: Draw a line segment AB = 4 cm. Taking point A as centre, draw an arc of 5 cm radius. Again, taking point B as centre, draw an arc of 6 cm. These arcs intersect each other at point C. So, we have AC = 5 cm and BC = 6 cm. ΔABC is the required triangle.
Step 1: Draw a line segment AB = 4 cm. Taking point A as centre, draw an arc of 5 cm radius. Again, taking point B as centre, draw an arc of 6 cm. These arcs intersect each other at point C. So, we have AC = 5 cm and BC = 6 cm. ΔABC is the required triangle.
Step 2: Draw a ray AX making an acute angle with line AB on the opposite side of vertex C.
Step 3: Locate 3 points A1, A2, A3 on AX such that AA1 = A1A2 = A2A3.
Step 4: Join the points B and A3.
Step 5: Through the point A2, draw a line parallel to BA3 intersecting AB at point B'.
Step 6: Draw a line through B' parallel to the line BC to intersect AC at C'. The required triangle is ΔAB'C'.
OR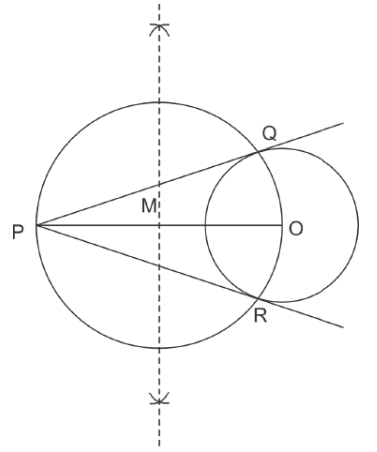 Steps of Construction:
Steps of Construction:
Step 1: Draw a circle of radius 2.5 cm with centre at point O. Locate a point P, at a distance of 8 cm from O, and join O and P.
Step 2: Bisect OP. Let M be the mid-point of OP.
Step 3: Draw a circle with centre at M and MO as radius. Q and R are points of intersections of this circle with the circle having centre at O.
Step 4: Join PQ and PR. PQ and PR are the required tangents.
Q.33. Prove that: (3 Marks)
cosec A – sin A sec A – cos A =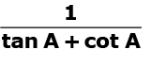
Ans. L.H.S. (cosec A sin A) (sec A cos A)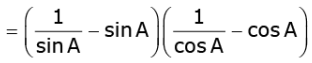
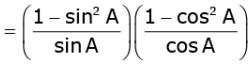
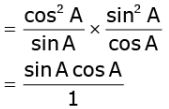
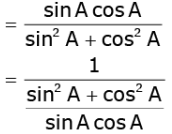
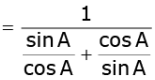
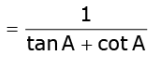
= R.H.S.
Q.34. In Figure – 4, AB and CD are two diameters of a circle (with centre O) perpendicular to each other and OD is the diameter of the smaller circle. If OA = 7 cm, then find the area of the shaded region. (3 Marks)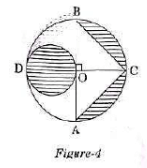 OR
OR
In Figure – 5 ABCD is a square with side 7 cm. A circle is drawn circumscribing the square. Find the area of the shaded region. (3 Marks)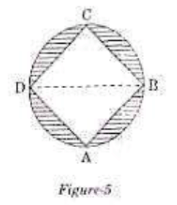 Ans. For bigger circle, OA = 7 cm
Ans. For bigger circle, OA = 7 cm
Diameter of the smaller circle = 7 cm
Radius of the smaller circle = 7 / 2 cm
Area of the smaller circle 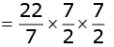
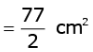
Area of shaded region
= Area of the smaller circle + 2 x Area of segment OCB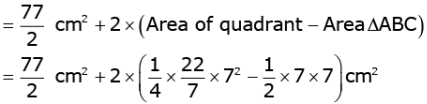
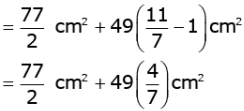
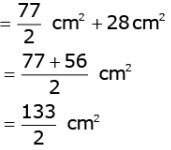
= 66.5cm2
OR
ABCD is a square with side 7 cm. Then,
Length of the diagonal of square = 7√2 cm
Diameter of circle = Diagonal of square
⇒ BD = 7√2 cm
Radius of circle = 7√2 / 2 cm
Area of shaded region = Area of circle - Area of the square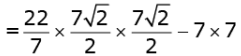
= 77 - 49
= 28 cm2
Therefore, the area of the shaded region is 28 cm2.
Section - D
Question numbers 35 to 40 carry 4 marks each.
Q.35. Find other zeroes of the polynomial (4 Marks)
p x = 3x4 - 4x3 - 10x2 +8x + 8,
if two of its zeroes are √2 and - √2.
OR
Divide the polynomial g x = x3 - 3x2 + x + 2 by the polynomial x2 - 2x + 1 and verify the division algorithm. (4 Marks)
Ans. The given polynomial is p(x) = 3x4 - 4x3 - 10x2 + 8x + 8
The two zeroes of p(x) are √2 and - √2.
Therefore, (x - √2) and (x + √2) are factors of p(x).
Also, (x - √2)(x + √2) = x2 - 2
and so x2 - 2 is a factor of p(x).
Now,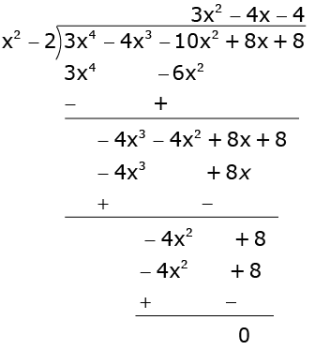
3x4 - 4x3 - 10x2 + 8x + 8 = (x2 - 2) (3x2 - 4x - 4)
= (x2 - 2)(3x2 - 6x + 2x - 4)
= (x2 - 2)(3x + 2)(x - 2)
Equating (x2 - 2)(3x + 2)(x - 2) to zero, we get the zeroes of the given polynomial.
Hence, the zeroes of the given polynomial are : √2, -√2, - 2 / 3 and 2.
OR
The given polynomial is g(x) = x3 - 3x2 + x + 2.
Here, divisor is x2 - 2x + 1.
Divide g(x) = x3 - 3x2 + x + 2 by x2 - 2x +1 and find the remainder.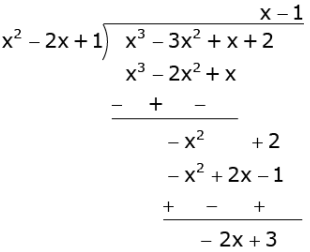
So, Quotient = x - 1 and Remainder = -2x + 3.
The division algorithm states that
Dividend = Divisor x Qoutient + Remainder
RHS = Divisor x Qoutient + Remainder
= (x2 - 2x + 1) (x - 1) - 2x + 3
= x3 - 2x2 + x - x2 + 2x -1 - 2x + 3
= x3 - 3x2 + x + 2 = LHS
Thus, the division alogorithm is verified.
Q.36. From the top of a 75 m high lighthouse from the seal level, the angles of depression of two ships are 30°and 45° if the ships are on the opposite sides of the lighthouse, then find the distance between the two ships. (4 Marks)
Ans. Let AB be a lighthouse and ships be at points C and D. It is given that AB 75 m. We have to find the distance CD.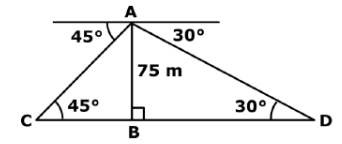 In ΔABC, we have AB
In ΔABC, we have AB
tan45° = AB / BC
or 1 = AB / BC
or BC = AB = 75...... (1)
Now,
In ΔABD, we have
tan30° = AB / BD
or 1 / √3 = 75√3
or BD = 75√3...... (2)
From (1) and (2), we get
CD = BC + BD = 75 + 75√3 = 75 (1+ √3)
Therefore, the distance between the two ships is 75(1 + √3) m.
Q.37. If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, prove that the other two sides are divided in the same ratio. (4 Marks)
OR
In Figure-6, in an equilateral triangle ABC, AD ⊥ BC, BE ⊥ AC and CF ⊥ AB. Prove that 4(AD2 + BE2 + CF2) = 9AB2. (4 Marks) Ans.
Ans.
Given: In ΔABC, DE || BC.
To Prove: AD / DB = AE / EC.
Construction:
(i) Join BE and CD.
(ii) Draw DM ⊥ AC and EN ⊥ AB.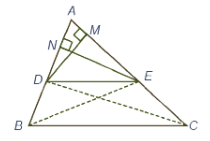 Proof:
Proof:
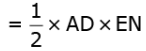
and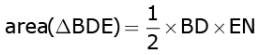
Therefore,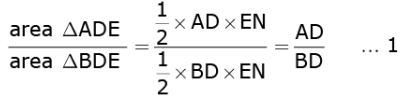
Similarly,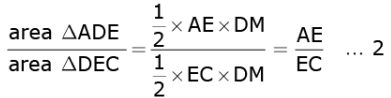
But area (ΔBDE) = area(ΔDEC)...(3)
Therefore, from (1), (2) and (3), we get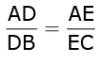
Hence, proved.
OR
ABC is an equilateral triangle.
Therefore, AB = BC = AC
Now,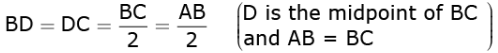
Using Pythagoras theorem in ΔADC, we get
AC2 = AD2 + DC2
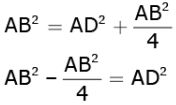
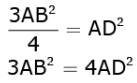 ......(1)
......(1)
Similarly, using Pythagoras theorem in ΔAEB, we get
3AB2 = 4BE2 ...... (2)
Again, using Pythagoras theorem in ΔAFC, we get
3AB2 = 4CF2......(3)
On adding equations (1), (2) and (3) we get
3AB2 + 3AB2 + 3AB2 = 4AD2 + 4BE2 + 4CF2
or, 9AB2 = 4 AD2 + BE2 + CF2
or, 4 AD2 + BE2 + CF2 = 9AB2
Hence, proved.
Q.38. A container open at the top and made up of a metal sheet, is in the form of a frustum of a cone of height 14 cm with radii of its lower and upper circular ends as 8 cm and 20 cm. respectively. Find the capacity of the container. (4 Marks)
Ans. Height of the frustum = h = 14 cm
Radius of upper end of the frustum = r = 20 cm
Radius of lower end of the frustum = r2 = 8 cm
Capacity of container = Volume of the frustum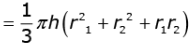
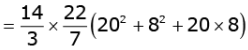
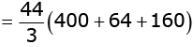
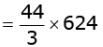
= 9125cm3
Q.39. Two water taps together can fill a tank in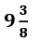 hours. The tap of larger diameter takes 10 hours less than the smaller one to fill the tank separately. Find the time in which each tap can separately fill the tank. (4 Marks)
hours. The tap of larger diameter takes 10 hours less than the smaller one to fill the tank separately. Find the time in which each tap can separately fill the tank. (4 Marks)
OR
A rectangular park is to be designed whose breadth is 3 m less than its length. Its area is to be 4 square metres more than the area of a park that has already been made in the shape of an isosceles triangle with its base as the breadth of the rectangular park and of altitude 12 m. Find the length and breadth of the park. (4 Marks)
Ans. Let A and B be the time taken by the smaller and the larger taps respectively to fill the tank.
Since both the taps together can fill the tank in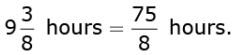
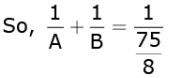
Or, 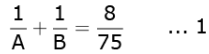
Tap with larger diameter takes 10 hours less than smaller one to fill the tank.
So, A - 10 = B
Or, 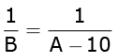 ....(2)
....(2)
By placing the value of 1 / B from 2 in to 1, we get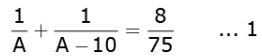

Or, 75A - 375 = 4A2 - 40A
Or, 4A2 - 40A - 75A + 375 = 0
Or, 4A2 - 115A + 375 = 0
Or, 4A2 - 100A - 15A + 375 = 0
Or, 4A (A - 25) -15 (A - 25) = 0
Or, (A - 25)(4a - 15) = 0.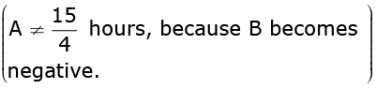
So, B = 25 - 10 = 15 hours
OR
Let L be the length of the rectangle.
So, breadth of the rectangle = L - 3
Area of the rectangle = L L - 3.....1
Base of the isosceles triangle = L - 3
Altitude of the isosceles triangle = 12 m
Area of the isosceles triangle = 1 / 2 (12) (L - 3) .....(2)
Given that
L(L - 3) = 1 / 2 (12) (L - 3) + 4
Or, L2 - 3L = 6L - 18 + 4
Or, L2 - 9L + 14 = 0
Or, L2 - 7L - 2L + 14 = 0
Or, L(L - 7) + 2(L - 7) = 0
Or, (L - 7)(L - 2) = 0
So, L = 7m (L ≠ 2 ∵ L - 3 is negative.)
Breadth = 7m - 3m = 4m
Length and breadth of the rectangle are 7m and 4m respectively.
Q.40. Draw a 'less than' ogive for the following frequency distribution: (4 Marks)
Ans.
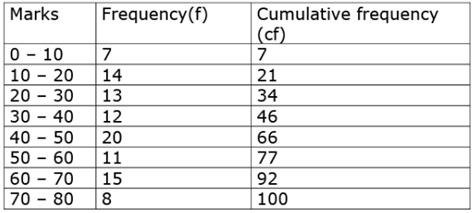
Now, plot (10, 7), (20, 21), …, (80, 100) on the graph.
|
126 videos|457 docs|75 tests
|
FAQs on Math Past Year Paper with Solution - 2020, Class 10 - (Basic) - Mathematics (Maths) Class 10
| 1. What is the importance of solving past year papers for the Class 10 Math exam? |  |
| 2. How can solving past year papers help in improving performance in the Class 10 Math exam? |  |
| 3. Are the solutions provided for the Class 10 Math past year papers accurate and reliable? |  |
| 4. How should I effectively utilize the Class 10 Math past year papers for exam preparation? |  |
| 5. Can solving the Class 10 Math past year papers guarantee success in the exam? |  |

|
Explore Courses for Class 10 exam
|

|


















