Math Past Year Paper with Solution - 2020, Class 10 - (Standard) | Mathematics (Maths) Class 10 PDF Download
| Table of contents |

|
| General Instructions |

|
| Section - A |

|
| Section - B |

|
| Section - C |

|
| Section - D |

|
Class X
Mathematics – Standard
Max. Marks: 80
Duration: 3 hrs.
General Instructions
Read the following instructions very carefully and strictly follow them:
This question paper comprises four sections – A, B, C and D. This question. Paper carries 40 questions. All questions are compulsory.
- Section A: Question Number 1 to 20 comprises of 20 questions of one mark each.
- Section B: Question Number 21 to 26 comprises of 6 questions of two marks each.
- Section C: Question Number 27 to 34 comprises of 8 questions of three marks each.
- Section D: Question Number 35 to 40 comprises of 6 questions of four marks each.
- There is no overall choice in the question Paper. However, an internal choice has been provided in 2 questions of one mark, 2 questions of two marks, 3 questions of three marks and 3 questions of four marks. You have to attempt only one of the choices in such questions.
- In addition to this, separate instructions are given with each section and question, wherever necessary.
- Use of calculators is not permitted.
Section - A
Question numbers 1 to 20 carry 1 mark each. Question numbers 1 to 10 are multiple choice questions.
Q.1. On dividing a polynomial p(x) by x2 – 4, quotient and remainder are found to be x and 3 respectively. The polynomial p(x) is
(a) 3x2 + x - 12
(b) x3 - 4x + 3
(c) x2 + 3x - 4
(d) x2 - 4x - 3
Ans. b
Solution. P(x) = (divisor)×(quotient) + Remainder
=(x2 – 4)x + 3
= x3 – 4x + 3
Q.2. In Figure-1, ABC is an isosceles triangle, right angled at C. Therefore
(a) AB2 = 2AC2
(b) BC2 = 2AB2
(c) AC2 = 2AB2
(d) AB2 = 4AC2
Ans. a
Solution. Given that ACB is an isosceles triangle right angled at C.
Therefore, AC = BC Using Pythagoras theorem in the given triangle, we have
AB2 = AC2 + BC2
= AC2 + AC2
= 2AC2
Q.3. The point on the x-axis which is equidistant from (─ 4, 0) and 10, 0) is
(a) (7, 0)
(b) (5, 0)
(c) (0, 0)
(d) (3, 0)
Ans. d
Solution. The required point and the given points as well lie on the x-axis.
The required point (x, 0) is the mid-point of the line joining points (–4, 0) and (10, 0).
So, x = (– 4+10)/2
= 6/2
= 3
Required point = (x, 0)
= (3, 0)
OR
The centre of a circle whose end points of a diameter are (─ 6, 3) and 6, 4) is
(a) (8, ─ 1)
(b) (4, 7)
(c) 0, 7/2
(d) 4, 7/2
Ans. c
Solution. The centre of a circle is the mid-point of its diameter.
End points of the diameter are: (–6, 3) and (6, 4)
Coordinates of the centre = ((– 6+6)/2, (3+4)/2)
= (0, 7/2)
Q.4. The value(s) of k for which the quadratic equation 2x2 + kx + 2 = 0 has equal roots, is
(a) 4
(b) ± 4
(c) ─ 4
(d) 0
Ans. b
Solution. The given equation is:
2x2 + kx + 2 = 0
Discriminant = b2 – 4ac
Here, b = k, a = 2, and c = 2
So, Discriminant = k2 – 4 × 2 × 2
= k2–16
A quadratic equation has equal roots if its discriminant is zero.
k2 – 16 = 0
k2 = 16
k = ±4
Q.5. Which of the following is not an A.P.?
(a) ─ 1.2, 0.8, 2.8
(b) 3, 3 + √2 , 3 + 2√2 , 3 + 3√2, ____
(c) 4/3, 7/3, 9/3, 12/3, ____
(d) -1/5, -2/5, -3/5, ____
Ans. c
Solution.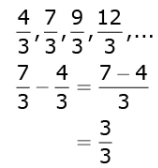
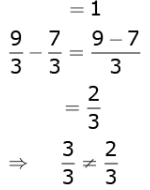
Difference between consecutive terms is not same. So, this is not an A.P.
Q.6. The pair of linear equations 3x/2 + 5y/3 = 7 and 9x + 10y = 14 is 23
(a) consistent
(b) inconsistent
(c) consistent with one solution
(d) consistent with many solutions
Ans. b
Solution.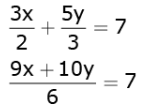
9x + 10y 42 ...(1)
9x + 10y 14 ...(2)
Ratios of coefficients of x and that of y are
9/9 = 10/10 = 1/1
Ratio of constants = 42/14 = 3/1 ≠ 1/1
Ratios of coefficients of x and y are equal but they are not equal to the ratio of constants.
So, the given equations represent a pair of parallel lines and so they do not have a common solution.
Q.7. In Figure-2 PQ is tangent to the circle with centre at O, at the point B. If √AOB = 100°, then √ABP is equal to
(a) 50°
(b) 40°
(c) 60°
(d) 80°
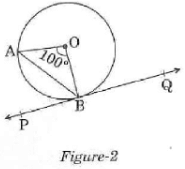
Ans. a
Solution. OA = OB (radii)
So, ∠OAB = ∠OBA
= (180° –100°)/2
= 40°
Now, a radius of a circle meets a tangent at 90°.
So, ∠ABP = ∠OBP – ∠OBA = 90° –40° = 50°
Q.8. The radius of a sphere (in cm) whose volume is 12π cm3, is
(a) 3
(b) 3√3
(c) 32/3
(d) 31/3
Ans. c
Solution.
Volume of sphere = 4/3 πr3
12π = 4/3 πr3
r3 = 32
r = 32/3
Q.9. The distance between the points (m,–n) and (–m, n) is
(a) 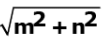
(b) m + n
(c) 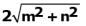
(d) 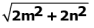
Ans. c
Solution.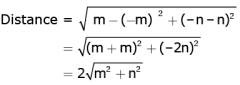
Q.10. In Figure-3. From an external point P, two tangents PQ and PR are drawn to a circle of radius 4 cm with centre O. If ∠QPR = 90°, then length of PQ is
(a) 3cm
(b) 4cm
(c) 2cm
(d) 2√2cm
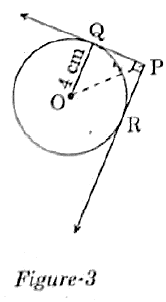
Ans. b
Solution. Tangents are drawn from an external point P.
So, line joining centre O and point P bisects ∠PQR.
OP bisects ∠QPR = 90°.
In ∆ OQP, ∠Q = 90° (radius meets tangent at 90°)
∠QPO = 45° = ∠QOP
Thus, OQ = PQ = 4 cm
Fill in the blanks in question number 11 to 15
Q.11. The probability of an event that is sure to happen is ______.
Ans. 1
Q.12. Simplest form of 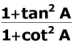 is ______.
is ______.
Ans.
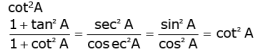
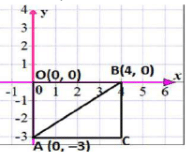
Q.13. AOBC is a rectangle whose three vertices are A(0, –3), O(0, 0) and B (4, 0). The length of its diagonal is ______.
Ans. In right-angled triangle AOB,
Q.14. In the formula 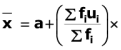 h, u = _____.
h, u = _____.
Ans.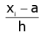
Q.15. All concentric circles are ______ to each other.
Ans. Similar
Answer the following question numbers 16 to 20.
Q.16. Find the sum of the first 100 natural numbers.
Ans. 1+ 2 + 3 ....100 is an A. P.
Here first term a = 1
Common difference d = 1
Sum of n terms of an A.P. = 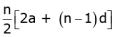
The sum of first 100 natural numbers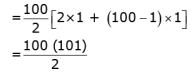
= 50 x 101
= 5050
Q.17. In Figure-4 the angle of elevation of the top of a tower from a point C on the ground, which is 30 m away from the foot of the tower, is 30°. Find the height of the tower.
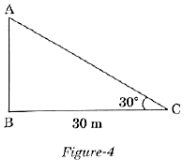
Ans.
tan30º = AB/30
1/√3 = AB/30
= AB = 30/√3 = 10√3
So, the height of the tower is 10√3 m.
Q.18. The LCM of two numbers is 182 and their HCF is 13. If one of the numbers is 26, Find the other.
Ans. LCM HCF Pr oduct of the two numbers
182 × 13 = 26 × x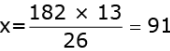
So, the other number is 91.
Q.19. Form a quadratic polynomial, the sum and product of whose zeroes are (-3) and 2 respectively.
Ans. x2 – (sum of zeroes) x + product of zeroes
= x2 – (–3)x + 2
= x2 + 3x + 2
So, the required polynomial is x2 + 3x + 2.
OR
Can (x2 – 1) be a remainder while dividing x4 – 3x2 + 5x – 9 by (x2 +3)? Justify your answer with reasons.
Ans. When a polynomial p(x) is divided by another polynomial g(x), then the degree of remainder r(x) < degree of g(x)
Therefore, for the given question x2 – 1 cannot be a remainder while dividing x4 – 3x2 + 5x – 9 by x2 + 3 because deg (x2 – 1) = deg (x2 + 3).
Q.20. Evaluate: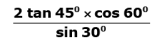
Ans.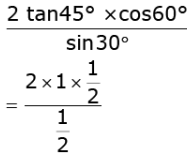
= 2
Section - B
Question number 21 to 26 carry 2 marks each.
Q.21. In the given Figure-5, DE ||AC and DF||AE.
Prove that BF/FE = BE/EC.

Ans. In ABC, DE AC
So, using basic proportionality theorem, we get
BD/DA = BE/EC ...(1)
In ΔBAE, DF║AE
So, using basic proportionality theorem, we get
BD/DA = BF/FE ...(2)
From (1) and (2), we get
BE/EC = BF/FE
Q.22. Show that 5 + 2√7 is an irrational number, where 7 is given to be an irrational number.
Ans.
Let us assume, to the contrary, that 5 + 2√7 is rational.
That is, we can find coprime a and b (b ≠ 0) such that
5 = 2√7 = a/b
∴ 2√7 = a/b - 5
Rearranging this equation, we get √7 = 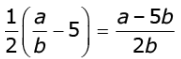
Since, and are integers, we get a - 5b/2b is rational, and 2 so √7 is a rational.
But this contradicts the fact that 7 is irrational.
This contradiction has arisen because of our incorrect assumption that 5 + 2√7
is rational. So, we conclude that 5 + 2√7 is irrational.
OR
Check whether 12n can end with the digit 0 for any natural number n.
Ans. If the number 12 , for any , were to end with the digit zero, then it would be divisible by 5.
That is, the prime factorisation of 12n would contain the prime 5. This is not possible 12 = ∵ 12n = (2 × 2 × 3)n
So, the prime numbers in the factorisation of 12n are 2 and 3.
So, the uniqueness of the Fundamental Theorem of Arithmetic guarantees that there are no other primes in the factorisation of 12n .
So, there is no natural number n for which 12n ends with the digit zero.
Q.23. If A, B and C are interior angles of a Ð ABC, then show that 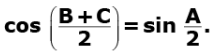
Ans. Given that A, B and C are interior angles of a triangle ABC.
∴ A + b + c = 180º
or A = 180º - B - C
Now,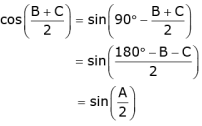
Q.24. In Figure 6, a quadrilateral ABCD is drawn to circumscribe a circle.
Prove that
AB + CD = BC +AD.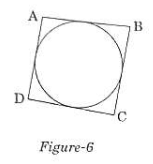
Ans.
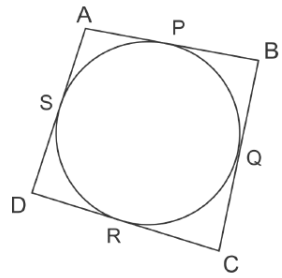
We have to prove that
AB + CD + BC + AD
We know that lengths of tangents drawn from a point to a circle are equal.
Therefore, from figure, we have
DR = DS, CR = CQ, AS = AP, BP = BQ
Now,
LHS = AB + CD = (AP + BP) + (CR + DR)
= (AS BQ) (CQ + DS)
= BQ + CQ + AS + DS
= BC + AD
RHS
OR
In Figure-7, find the perimeter of √ABC, if AP = 12 cm.

Ans. From the given figure, we have AP = 12 cm
Since AQ and AB are the tangent to the circle from a common point A, hence AP = AQ = 12
Similarly, PB = BD and CD = CQ
Also, AP = AB + PB and AQ = AC + CQ
Perimeter of ABC = AB + BD + CD + AC
= AB + PB + CQ + AC
(since PB = BM and CM = CQ)
= (AB + PB) + (CQ + AC)
= AP + AQ
= 12 +12
= 24 cm
Therefore, the perimeter of triangle ABC =24 cm
Q.25. Find the mode of the following distribution:
Ans.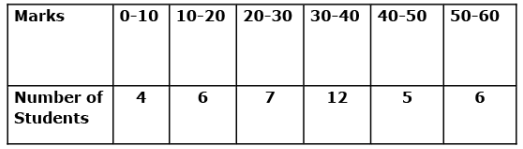
From the given data, we have
I = 30, f1 = 12, f0 = 7, f2 = 5, h = 10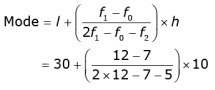
= 34.1667
∴ Mode of the given data is 34.1667.
Q.26. 2 cubes, each of volume 125 cm3, are joined end to end. Find the surface area of the resulting cuboid.
Ans. Let the side of the old cube = a
The volume of the old cube = 125 cm3 (Given)
The volume of the cube = a3
a = 125 cm3
a3 = 53
a = 5 cm
The dimensions of the resulting cuboid are: Length,
l = 10 cm
Breadth, b = 5
Height, h = 5 cm
Total surface area of the resulting cuboid:
= 2(lb + bh + hl)
= 2[10(5)+5(5)+5(10)]
= 2[50+25+50]
= 2[125]
= 250 cm2
Section - C
Q.27. A fraction becomes 1/3 when 1 is subtracted from the numerator and it becomes 1/4 when 8 is added to its denominator. Find the fraction.
Ans. Let the numerator of the fraction be x and denominator be y.
Therefore, the fraction is x/y.
According to question,
x - 1/y = 1/3
3x - 1 = y
3x - 3 = y ....(1)
and x/ y + 8 = 1/4
4x = y + 8
4x - 8 = y ....(2)
From equations 1 and 2, we get
3x - 3 = 4x - 8
4x - 3x = 8 -3
x = 5
Putting 5 in equation (1),
3x 5 - 3 = y
y = 12
So, the required fraction = 5/12
OR
The present age of a father is three years more than three times the age of his son. Three years hence the father's age will be 10 years more than twice the age of the son. Determine their present ages.
Ans. Let the son's present age be x.
So, father's present age = 3x + 3
3 years later:
Son's age = x + 3
Father's age = 3x + 3 + 3 = 3x + 6
But, according to the given condition,
3 years later father's age = 2 x + 3 + 10
2x + 6 + 10
2x + 16
So, we can write
3x + 6 = 2x + 16
3x - 2x = 16 - 6
x = 10
So, son's present age 10 years
and father's present age 10 x 3 + 3
= 33 years
Q.28. Use Euclid Division Lemma to show that the square of any positive integer is either of the form 3q or 3q + 1 for some integer q.
Ans. Let be a positive integer and 3.
By Euclid's Algorithm,
a = 3m + r for some integer m ≥ 0 and 0 ≤ r ≤ 3.
The possible remainders are 0, 1 and 2. Therefore,
a can be 3m or 3m + 1 or 3m + 2.
Thus,
a2 = 9m2 or (3m + 1)2 or (3m + 2)2
= 9m2 or (9m2+ 6m + 1) or (9m2 + 12m + 4)
= 3x (3m2) or 3(3m2 + 2m) + 1 or 3(3m2 + 4m + 1) + 1
3k1 or 3k2 + 1 or 3k3 + 1
where k1, k2 and k3 are some positive integers.
Hence, square of any positive integer is either of the form 3q or 3q + 1 for some integer q.
Q.29. Find the ratio in which y-axis divides the line segment joining the points (6, - 4) and (-2, -7). Also find the point of intersection.
Ans. Let the ratio in which the line segment joining A (6, -4) and B (-2, 7) is divided by the y-axis be k:1.
Let the coordinate of point on y-axis be (0, y).
Therefore,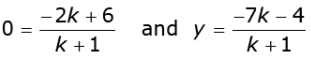
Now
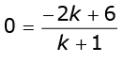
or 0 = -2k + 6
or k = 3
Therefore, the required ratio is 3:1.
Also,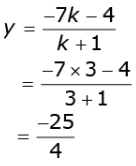
Therefore, the given line segment is divided by the point (0, -25/4) in the ratio 3:1.
OR
Show that the points (7, 100, (-2, 5) and (3, -4) are vertices of an isosceles right triangle.
Ans. Let the given points are P(7, 10), Q(-2, 5) and R(3, 4).
Now, using distance formula we find distance between these points i.e., PQ, QR and PR.
Distance between points P(7, 10) and Q(-2, 5),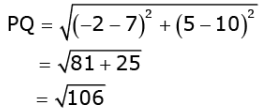
Distance between points Q(-2, 5) and R(3, 4),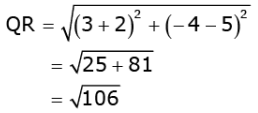
Distance between points P(7, 10) and R(3, 4),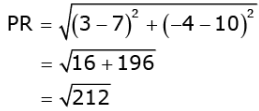
Now,
PQ2 + QR2 106 + 106
= 212 = PR2
i.e., PQ2 + QR2 = PR2
Therefore, points P(5, 2), Q(6, 4) and R(7, 2) form an isosceles right triangle because sides PQ and QR are equal.
Q.30. Prove that:
Ans.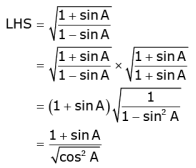
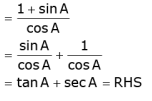
Q.31. For an A.P., it is given that the first term (a) = 5, common difference (d) = 3, and the nth term (an) = 50. Find n and sum of first n terms (Sn) of the A.P.
Ans. Here, a = 5, d = 3, an = 50
We need to find Sn.
Firstly, we will find the value of n.
We know that
an = a + (n - 1)d
So, 50 = 5 + (n - 1)3
or 50 - 5 (n - 1)3
or 45/3 + 1 = n
or n = 16
We know that sum of first n terms of an AP is given by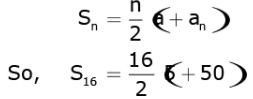
= 8 x 55
or s16 = 440
Q.32. Construct a ΔABC with sides BC = 6 cm, AB = 5 cm and ∠ABC= 60°. Then construct a triangle whose sides are 3/4 of the corresponding sides of ΔABC.
Ans.
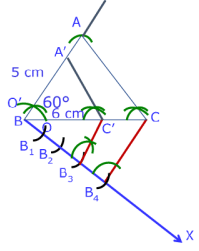
Steps of Construction :
Step 1: Draw a ∠ABC with sides AB 5 cm, BC 6 cm and ∠ABC 60º.
Step 2: Draw a ray BX making an acute angle with line BC on the opposite side of vertex A.
Step 3: Locate 4 points B1 , B2 , B3 , B4 on BX such that BB1 = B1B2 = B2B3 = B3B4.
Step 4: Join the points C and B4.
Step 5: Through the point B3, draw a line parallel to CB4 intersecting line segment BC at point C'.
Step 6: Draw a line through C' parallel to the line AC' to intersect line segment AB at A'. The required triangle is ΔA'BC'.
OR
Draw a circle of radius 3.5 cm. Take a point P outside the circle at a distance of 7 cm from the centre of the circle and construct a pair of tangents to the circle from that point.
Ans.

Steps of Construction:
Step 1: Draw a circle of radius 3.5 cm with centre at point O. Locate a point P, at a distance of 7 cm from O, and join O and P.
Step 2: Bisect OP. Let M be the mid-point of OP.
Step 3: Draw a circle with centre at M and MO as radius. Q and R are points of intersections of this circle with the circle having centre at O.
Step 4: Join PQ and PR. PQ and PR are the required tangents.
Q.33. Read the following passage and answer the question given at the end: Diwali Fair.
A game in a booth at a Diwali Fair involves using a spinner first. Then, if the spinner stops on an even number, the player is allowed to pick a marble from a bag. The spinner and the marbles in the bag are represented in Figure – 8.
Prizes are given when a black marble is picked. Shweta plays the game once.
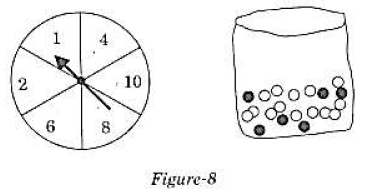
(i) What is the probability that she will be allowed to pick a marble from the bag?
(ii) Suppose she is allowed to pick a marble from the bag, what is the probability of getting a prize, when it is given that the bag contains 20 balls out of which 6 are black?
Ans. Numbers on spinner 1, 2, 4, 6, 8, 10
Even numbers on spinner 2, 4, 6, 8, 10
Shweta will pick black marble, if spinner stops on even number.
Therefore,
n(Even number) = 5
n(Possible number) = 6
(i) P Shweta allowed to pick a marble,
= P (Even number)
= n(Even number)/n(Possible number)
= 5/6
Therefore, the probability of allowing Shweta to pick a marble is 5/6.
(ii) Since, prizes are given, when a black marble is picked.
Number of black marbles = 6
Total number of marbles = 20
Therefore, P(getting a prize) = P(a black marble)
= n(Black marbles)/n(Total marbles)
= 6/20
= 3/10
Therefore, the probabiltiy of getting prize is 3/10.
Q.34. In figure – 9, a square OPQR is inscribed in a quadrant OAQB of a circle. If the radius of circle is 6√2 cm, find the area of the shaded region.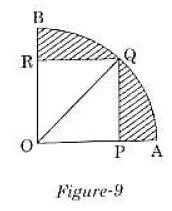
Ans.
Given that, OQ = 6√2 cm
OPQR is a square.
Let the side of square = a
The diagonal of square a√2
Here, OQ is a diagonal of square.
⇒ a√2 = 6√2
⇒ a = 6 cm
Area of square OPQR = 62
= 36 cm2
Radius of the quadrant OAQB = Diagonal of the square OPQR
= 6√2
Area of the quadrant OAQB = 90º/360º x 22/7 x (6√2)2
= 396/7 cm2
Area of shaded region = Area of the quadrant OAQB
- Area of square OPQR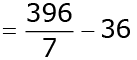
= 144/7
= 20.6 cm2
Section - D
Q.35. Obtain other zeroes of the polynomial
p(x) = 2x4 - x3 - 11x2 + 5x + 5
if two of its zeroes are √5 and - √5.
Ans. The given polynomial is p(x) = 2x4 - x3 - 11x2 + 5x + 5.
The two zeroes of p(x) are √5 and - √5.
Therefore, (x - √5 and (x + √5) are factors of p(x).
Also, (x - √5) (x + √5) = x2 - 5
and so x2 - 5 is a factor of p(x).
Now,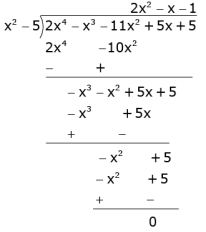
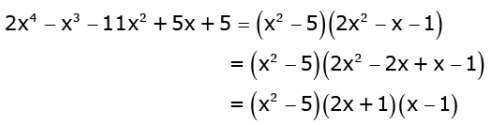
Equating (x2 - 5) (2x + 1) (x - 1) to zero, we get the zeroes of the given polynomial.
Hence, the zeroes of the given polynomial are : 1
√5, - √5, -1/2 and 1.
OR
What minimum must be added to 2x3 - 3x2 + 6x + 7 so that resulting polynomial will be divisible by x2 - 4x +8 ?
Ans. The given polynomial is 2x3 - 3x2 + 6x + 7.
Here, divisor is x2 - 4x + 8.
Divide 2x3 - 3x2 + 6x + 7 by x2 - 4x + 8 and find the remainder.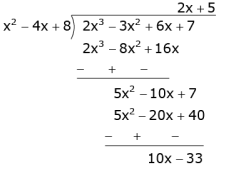
Remainder = 10x - 33
Therefore, we should add -(10x - 33) to make it exactly divisible by x2 - 4x + 8.
Thus, we should add 10x + 33 to 2x3 - 3x2 + 6x + 7.
Q.36. Prove that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
Ans. Given: ΔABC ∼ ΔDEF
To prove: 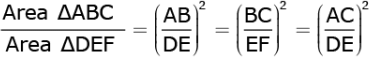
Construction: Draw AL ⊥ BC and DM ⊥ EF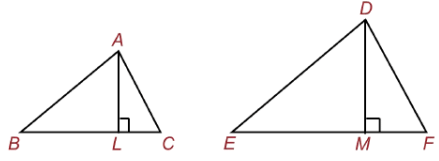
Proof here: 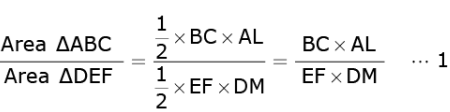
In ΔALB and ΔDME
∠ALB = ∠DME Each 90°
and √B = √E Since ΔABC ∼ ΔDEF
So, ΔALB ∼ ΔDME AA similarity criterion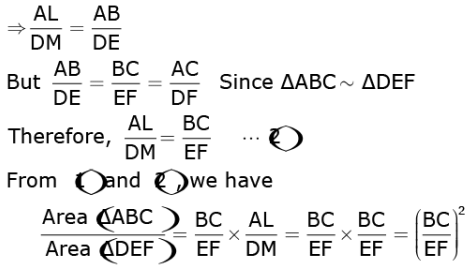
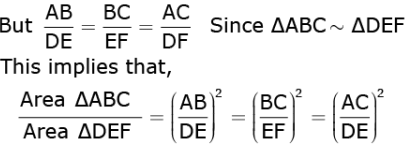
Q.37. Sum of the areas of two squares is 544m2. If the difference of their perimeters is 32 m, find the sides of the two squares.
Ans. Let the sides of first and second square be x any y. Then,
Area of first square = x2
And,
Area of second square = y2
According to the question,
x2 + y2 = 544 ...1
Now,
Perimeter of first square = 4x
And,
Perimeter of second square = 4y
According to the question,
4x – 4y = 32 ...(2)
From equation (2) , we get
4(x – y) = 32
or, x - y = 32/4
or, x - y = 8
or, x = 8 + y ...(3)
Subsituting this value of x in equation (1), we get
x2 + y2 = 544
or, (8 + y)2 + y2 = 544
or, 64 + y2 = 16y + y2 = 544
or, 2y2 + 16y + 64 = 544
or, 2y2 + 16y + 64 - 544 = 0
or, 2y2 + 16y - 480 = 0
or, 2(y2 + 8y - 240) = 0
or, y2 + 8y - 240) = 0
or, y2 + 20y - 12y - 240 = 0
or, y(y + 20) - 12 (y + 20) = 0
or, (y + 20) (y - 12) = 0
⇒ y + 20 = 0 or y - 12 = 0
⇒ y = -20 or y = 12
Since side of a square cannot be negative, therefore y = 12.
Substituting y = 12 in equation (3), we get
x = 8 + y = 8 + 12 = 20
Therefore,
Side of first square = x = 20 cm
And,
Side of second square = y = 12 cm
OR
A motorboat whose speed is 18km/h in still water takes 1 hour more to go 24 km upstream than to return downstream to the same spot. Find the speed of the stream.
Ans. Let the speed of the stream be x km/h.
Therefore, speed of the boat upstream = (18 – x) km/h
and the speed of the boat downstream = (18 + x) km/h.
The time taken to go upstream = distance/speed
= 24/18 - x hours.
Similarly, the time taken to go downstream = 24/18 - x hours.
According to the question,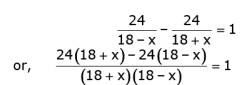
or, 24/18 + x) - 24(18 - x) = (18 + x) (18 - x)
or, 432 + 24x - 432 + 24x = 324 - x2
or, x2 + 48x - 324 = 0
Using the quadratic formula, we get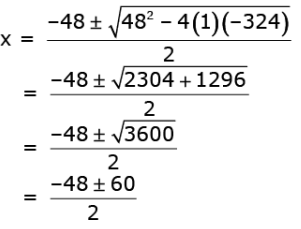
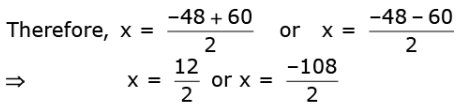
⇒ x = 6 or x = –54
Since x is the speed of the stream, it cannot be negative.
So, we ignore the root x = –54. Therefore, x = 6 gives the speed of the stream as 6 km/h.
Q.38. A solid toy is in the form of a hemisphere surmounted by a right circular cone of same radius. The height of the cone is 10 cm and the radius of the base is 7 cm. Determine the volume of the toy. Also find the area of the coloured sheet required to cover the toy.
(Use π = 22/7 and 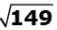 12.2)
12.2)
Ans.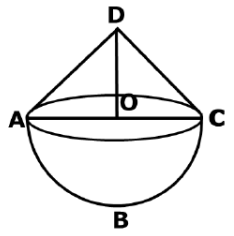
Let ABC be the hemisphere and ADC be the cone standing on the base of the hemisphere.
Height of the cone (h1) = 10 cm (Given)
Radius of the cone (r1) = 7 cm (Given)
Since the hemisphere is surmounted by the right circular cone of same radius, therefore
Radius of the hemisphere (r2) = 7 cm
So,
Volume of the toy = Volume of the cone + Volume of the hemisphere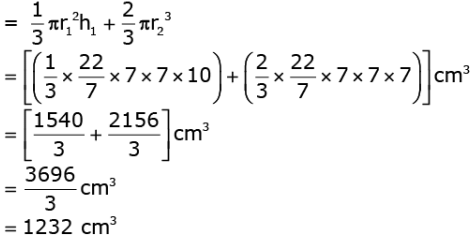
Area of the coloured sheet required to cover the toy
= CSA of hemisphere + CSA of cone
= 2πr22 + πrl
Where l is the slant height of the cone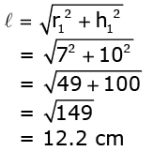
So,
Area of the coloured sheet required to cover the toy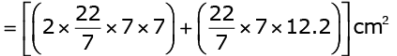
= (308 + 268.4)cm2
= 576.4 cm2
Q.39. A statue 1.6 m tall, stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 600 and from the same point the angle of elevation of the top of the pedestal is 450. Find the height of the pedestal.
(Use √3 = 1.73)
Ans.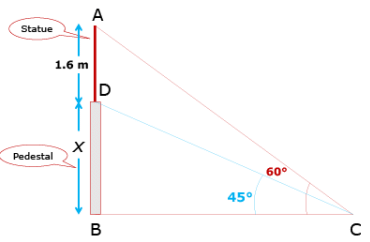
Let BD be a pedestal of height x m and AD be a statue of height 1.6 m. The angle of elevation of the top of pedestal from a point C is 45° and that of point statue from C is 60°.
In the triangle ABC:
AB/BC = tan60°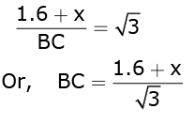 ....(1)
....(1)
In the triangle DBC:
DB/BC = tan45°
Or, x/BC = 1
Or, x = BC ...(2)
By equations 1 and 2 , we get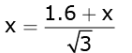
or, √3x = 1.6 + x
√3 - 1 x = 1.6
or,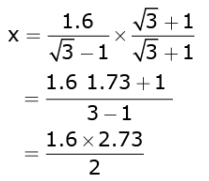
= 2.184 m
Therefore, the height of the pedestal is 2.184m.
Q.40. For the following data, draw a 'less than' ogive and hence find the median of the distribution.
Ans.
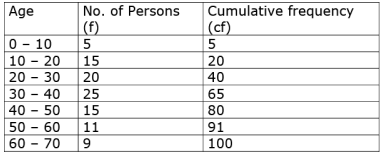
Plot the points (10, 5), (20, 20), …, (70, 100) on a graph paper.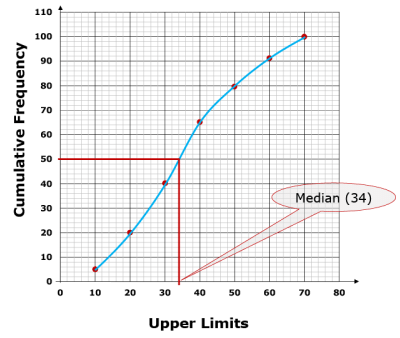
OR
The distribution given below show the number of wickets taken by bowlers in one-day cricket matches. Find the mean and the median of the number of wickets taken.
Ans.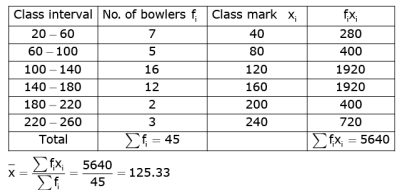
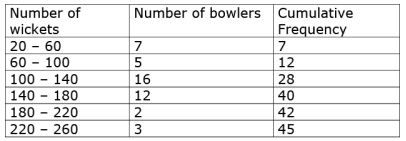
n = 45
⇒ n/2 = 45/2 = 2.5
Median class 100 - 140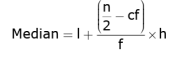
l = 100, n/2 = 22.5, cf = 12, f = 16, h = 40
= 100 + 26.25
= 126.25
|
126 videos|457 docs|75 tests
|
FAQs on Math Past Year Paper with Solution - 2020, Class 10 - (Standard) - Mathematics (Maths) Class 10
| 1. What is the format of the Class 10 Math exam in 2020? |  |
| 2. How many questions are there in Section A of the Class 10 Math exam? |  |
| 3. What types of questions can be expected in Section B of the Class 10 Math exam? |  |
| 4. Are there any long answer questions in Section C of the Class 10 Math exam? |  |
| 5. What is the significance of Section D in the Class 10 Math exam? |  |

|
Explore Courses for Class 10 exam
|

|


















