Integers (Exercise 1.1) RD Sharma Solutions | Mathematics (Maths) Class 7 PDF Download
Q.1. Determine each of the following products:
(i) 12 ☓ 7
(ii) (−15) ☓ 8
(iii) (−25) ☓ (−9)
(iv) 125 ☓ (−8)
Ans:
(i) 12 × 7 = 84
(ii) (−15) × 8 = −120
(iii) (−25) × (−9) = 225
(iv) 125 × (−8) = −1000
Q.2. Find each of the following products:
(i) 3 ☓ (−8) ☓ 5
(ii) 9 ☓ (−3) ☓ (−6)
(iii) (−2) ☓ 36 ☓ (−5)
(iv) (−2) ☓ (−4) ☓ (−6) ☓ (−8)
Ans:
(i) 3 × (−8) × 5 = −3×(8×5) = −120
(ii) 9 × (−3) × (−6) = 9× (3×6) = 162
(iii) (−2) × 36 × (−5) = 36 × (2×5) = 360
(iv) (−2) × (−4) × (−6) × (−8) = (2×4×6×8) = 384
Q.3. Find the value of:
(i) 1487 × 327 + (−487) × 327
(ii) 28945 × 99 − (−28945)
Ans:
(i) 1487 × 327 + (−487) × 327 = 327 (1487 − 487) = 327 ×1000 =327000
(ii) 28945 × 99 − (−28945) = 28945 (99 −(−1)) = 28945 (99 + 1) = 2894500
Q.4. Complete the following multiplication table:
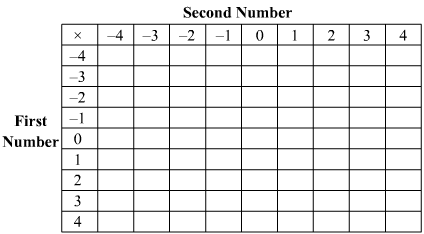
Is the multiplication table symmetrical about the diagonal joining the upper left corner to the lower right corner?
Ans:
| × | −4 | −3 | −2 | −1 | 0 | 1 | 2 | 3 | 4 |
| −4 | 16 | 12 | 8 | 4 | 0 | −4 | −8 | −12 | −16 |
| −3 | 12 | 9 | 6 | 3 | 0 | −3 | −6 | −9 | −12 |
| −2 | 8 | 6 | 4 | 2 | 0 | −2 | −4 | −6 | −8 |
| −1 | 4 | 3 | 2 | 1 | 0 | −1 | −2 | −3 | −4 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | −4 | −3 | −2 | −1 | 0 | 1 | 2 | 3 | 4 |
| 2 | −8 | −6 | −4 | −2 | 0 | 2 | 4 | 6 | 8 |
| 3 | −12 | −9 | −6 | −3 | 0 | 3 | 6 | 9 | 12 |
| 4 | −16 | −12 | −8 | −4 | 0 | 4 | 8 | 12 | 16 |
Yes, the table is symmetrical along the diagonal joining the upper left corner to the lower right corner.
Q.5. Determine the integer whose product with '−1' is
(i) 58
(ii) 0
(iii) −225
Ans: The integer, whose product with −1 is the given number, can be found by multiplying the given number by −1.
Thus, we have:
(i) 58 × (−1) = −58
(ii) 0 × (−1) = − (0×1) = 0
(iii) (−225) × (−1) = 225
Q.6. What will be the sign of the product if we multiply together
(i) 8 negative integers and 1 positive integer?
(ii) 21 negative integers and 3 positive integers?
(iii) 199 negative integers and 10 positive integers?
Ans: Negative numbers, when multiplied even number of times, give a positive number. However, when multiplied odd number of times, they give a negative number. Therefore, we have:
(i) (negative) 8 times × (positive) 1 time = positive × positive = positive integer
(ii) (negative) 21 times × (positive) 3 times = negative × positive = negative integer
(iii) (negative) 199 times × (positive) 10 times = negative × positive = negative integer
Q.7. State which is greater:
(i) (8 + 9) × 10 and 8 + 9 × 10
(ii) (8 − 9) × 10 and 8 − 9 × 10
(iii) {(−2) − 5} × (−6) and (−2) −5 × (−6)
Ans:
(i) ( 8 + 9) × 10 = 170 > 8 + 90 = 98
(ii) (8 − 9) × 10 = −10 > 8 − 90 = − 82
(iii) {(−2) − 5 } × (−6) = −7 × (−6) = 42 > (−2) − 5 × (−6) = ( −2 ) − (−30) = −2 + 30 = 28
Q.8. (i) If a × (−1) = −30, is the integer a positive or negative?
(ii) If a × (−1) = 30, is the integer a positive or negative?
Ans:
(i) a × (−1) = −30
When multiplied by a negative integer, a gives a negative integer. Hence, a should be a positive integer.
a = 30
(ii) a × (−1) = 30
When multiplied by a negative integer, a gives a positive integer. Hence, a should be a negative integer.
a = −30
Q.9. Verify the following:
(i) 19 × {7 + (−3)} = 19 × 7 + 19 × (−3)
(ii) (−23) {(−5) + (+19)} = (−23) × (−5) + (−23) × (+19)
Ans:
(i)
LHS = 19 × { 7 + (−3) } = 19 × {4} = 76
RHS = 19 × 7 + 19 × (−3) = 133 + (−57) = 76
Because LHS is equal to RHS, the equation is verified.
(ii)
LHS = (−23) {(−5) + 19} = (−23) { 14} = −322
RHS = (−23) × (−5) + (−23) × 19 = 115 + (−437) = −322
Because LHS is equal to RHS, the equation is verified.
Q.10. Which of the following statements are true?
(i) The product of a positive and a negative integer is negative.
(ii) The product of three negative integers is a negative integer.
(iii) Of the two integers, if one is negative, then their product must be positive.
(iv) For all non-zero integers a and b, a × b is always greater than either a or b.
(v) The product of a negative and a positive integer may be zero.
(vi) There does not exist an integer b such that for a> 1, a × b = b × a = b.
Ans:
(i) True. Product of two integers with opposite signs give a negative integer.
(ii) True. Negative integers, when multiplied odd number of times, give a negative integer.
(iii) False. Product of two integers, one of them being a negative integer, is not necessarily positive. For example, (−1) × 2 = −2
(iv) False. For two non-zero integers a and b, their product is not necessarily greater than either a or b. For example, if a = 2 and b = −2, then, a × b = −4, which is less than both 2 and −2.
(v) False. Product of a negative integer and a positive integer can never be zero.
(vi) True. If a > 1, then, a×b ≠ b×a ≠b
|
76 videos|344 docs|39 tests
|
FAQs on Integers (Exercise 1.1) RD Sharma Solutions - Mathematics (Maths) Class 7
| 1. What are integers? |  |
| 2. How are integers represented on a number line? |  |
| 3. What is the difference between positive and negative integers? |  |
| 4. How can we compare two integers? |  |
| 5. Can integers be used to represent real-life situations? |  |

|
Explore Courses for Class 7 exam
|

|


















