Integers (Exercise 1.4) RD Sharma Solutions | Mathematics (Maths) Class 7 (Old NCERT) PDF Download
Q.1. Simplify each of the following:
3 − (5 − 6 ÷ 3)
Ans: On applying the BODMAS rule, we get:
3 − (5 − 6 ÷ 3)
= 3 − (5 − 2) (On performing division)
= 3 − 3 (On performing subtraction)
= 0
Q.2. Simplify each of the following:
−25 + 14 ÷ (5 − 3)
Ans: On applying the BODMAS rule, we get:
−25 + 14 ÷ (5 − 3)
= −25 + 14 ÷ 2 (On simplifying brackets)
= −25 + 7 (On performing division)
= −18
Q.3. Simplify each of the following:
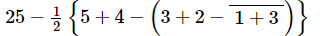
Ans: On applying the BODMAS rule, we get:
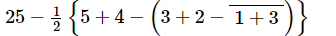
=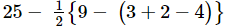 [Removing vinculum]
[Removing vinculum]
=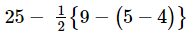 [Performing addition]
[Performing addition]
=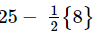 [Performing subtraction]
[Performing subtraction]
= 25− 4
= 21
Q.4. Simplify each of the following:
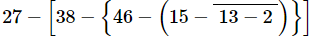
Ans: On applying the BODMAS rule, we get:
27 − [38 − {46 − (15 −11)}] (On simplifying vinculum)
= 27 − [38− {46 − 4}] (On simplifying parentheses)
= 27 − [38 − 42] (On simplifying braces)
= 27 − (−4) = 31
Q.5. Simplify each of the following:
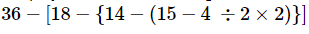
Ans: On applying the BODMAS rule, we get:
36 − [18 − { 14 − (15 − 4 ÷ 2 × 2)}]
= 36 − [18 − {14 − (15 − 2 × 2)}] (On performing division)
= 36 − [18 − {14 − (15 − 4)}] (On performing multiplication)
= 36 − [18 − {14 − 11}] (On simplifying parentheses)
= 36 − [18 − 3] (On simplifying braces)
= 36 − 15
= 21
Q.6. Simplify each of the following:
45 − [38 − {60 ÷ 3 − (6 − 9 ÷ 3) ÷ 3}]
Ans: On applying the BODMAS rule, we get:
45 − [38 − { 60 ÷ 3 − (6 − 9 ÷ 3) ÷ 3}]
= 45 − [38 − {60 ÷ 3 − (6 − 3) ÷ 3}] (On performing division)
= 45 − [38 − {60 ÷ 3 − 3 ÷ 3}] (On simplifying parentheses)
= 45 − [38 − {60 ÷ 3 − 1}] (On performing division)
= 45 − [38 − {20 − 1}] (On performing division)
= 45 − [38 − 19] (On performing subtraction)
= 45 − 19
= 26
Q.7. Simplify each of the following:
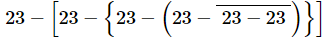
Ans: On applying the BODMAS rule, we get:
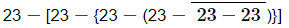
= 23 − [23 − {23 − (23 − 0}] (On simplifying vinculum)
= 23 − [23 − {23 − 23}] (On simplifying parentheses)
= 23 − [23 − 0] (On simplifying braces)
= 23 − 23 = 0
Q.8. Simplify each of the following:
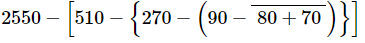
Ans: On applying the BODMAS rule, we get:
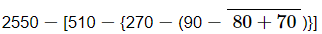
= 2550 − [510 − {270 − (90 − 150)}] (On simplifying vinculum)
= 2550 − [510 − { 270 − (− 60)}] (On simplifying parentheses)
= 2550 − [510 − 330] (On simplifying braces)
= 2550 − 180
= 2370
Q.9. Simplify each of the following:
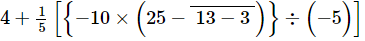
Ans: On applying the BODMAS rule, we get:
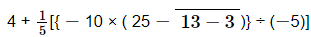
=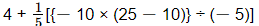 (On simplifying vinculum)
(On simplifying vinculum)
=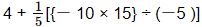 (On simplifying parentheses)
(On simplifying parentheses)
=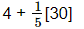 (On simplifying braces)
(On simplifying braces)
= 4 + 6
= 10
Q.10. Simplify each of the following:
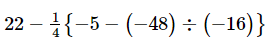
Ans: On applying the BODMAS rule, we get:
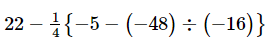
=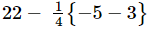 [Performing division]
[Performing division]
=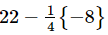
=22 − (−2) [Removing braces]
= 22 + 2 = 24
Q.11. Simplify each of the following:
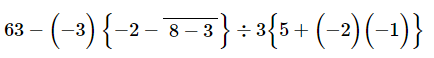
Ans: On applying the BODMAS rule, we get:
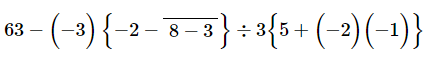
= 63 − (− 3) {− 2 − 5} ÷ 3 {5 + 2} (On simplifying vinculum)
= 63 − (− 3) (− 7 ) ÷ 3 × 7 (On simplifying braces)
= 63 − (21÷21)
= 63 − 1
= 62
Q.12. Simplify each of the following:
[29 − (−2){6 − (7 − 3)}] ÷ [3 × {5 + (−3) × (−2)}]
Ans: On applying the BODMAS rule, we get:
[29 − (− 2) {6 − (7 − 3)}] ÷ [3 × { − 3) × (− 2)}]
= [29 − (− 2) {6 − 4}] ÷ [3 × { 5 + 6}] (On simplifying parentheses)
= [29 − (− 2) (2)] ÷ [3 × 11] (On performing subtraction and addition)
= [29 + 4] ÷ 33 (On performing multiplication)
= 33 ÷ 33
= 1
Q.13. Using brackets, write a mathematical expression for each of the following:
(i) Nine multiplied by the sum of two and five.
(ii) Twelve divided by the sum of one and three.
(iii) Twenty divided by the difference of seven and two.
(iv) Eight subtracted from the product of two and three.
(v) Forty divided by one more than the sum of nine and ten.
(vi) Two multiplied by one less than the difference of nineteen and six.
Ans:
(i) 9 (2 + 5)
(ii) 12 ÷ (1 + 3)
(iii) 20 ÷ (7 − 2)
(iv) (2 × 3 ) − 8
(v) 40 ÷ {(9 + 10) + 1}
(vi) 2 × {(19 − 6) − 1}
Objective Type Questions
Q.1. Mark the correct alternatives in each of the following:
(−1) × (−1) × (−1) × (−1) × ... 500 times =
(a) −1
(b) 1
(c) 500
(d) −500
Ans: The number of integers in the given product is even.
∴ (−1) × (−1) × (−1) × (−1) × ... 500 times
= 1 × 1 × 1 × 1 × ... 500 times
= 1
Hence, the correct answer is option (b).
Q.2. Mark the correct alternatives in each of the following:
(−1) + (−1) + (−1) + (−1) + ... 500 times =
(a) 500
(b) 1
(c) −1
(d) −500
Ans: (−1) + (−1) + (−1) + (−1) + ... 500 times
= −(1 + 1 + 1 + 1 + ... 500 times)
= −500
Hence, the correct answer is option (d).
Q.3. Mark the correct alternatives in each of the following:
The additive inverse of −7 is
(a) −7
(b) −1/7
(c) 7
(d) 1/7
Ans: We know that, for every integer a, there exists integer −a such that
a + (−a) = 0 = −a + a
Here, −a is the additive inverse of a and a is the additive inverse of −a.
Now, 7 + (−7) = 0 = −7 + 7
∴ 7 is the additive inverse of −7.
Hence, the correct answer is option (c).
Q.4. Mark the correct alternatives in each of the following:
The modulus of an integer x is 9, then
(a) x = 9 only
(b) x = −9 only
(c) x = ± 9
(d) None of these
Ans: The modulus (or absolute value) of an integer is its numerical value regardless of its sign. The absolute value of an integer is always non-negative.
It is given that,
Modulus of x = | x | = 9
Now, | −9 | = 9 and | 9 | = 9
∴ x = −9 or x = 9
⇒ x = ± 9
Hence, the correct answer is option (c).
Q.5. Mark the correct alternatives in each of the following:
By how much does 5 exceed −4?
(a) 1
(b) −1
(c) 9
(d) −9
Ans: Difference between 5 and −4 = 5 − (−4) = 5 + 4 = 9
Thus, 5 exceed −4 by 9.
Hence, the correct answer is option (c).
Q.6. Mark the correct alternatives in each of the following:
By how much less than −3 is −7?
(a) 4
(b) −4
(c) 10
(d) −10
Ans: Difference between −3 and −7 = (−3) − (−7) = −3 + 7 = 4
Thus, −7 is less than −3 by 4.
Hence, the correct answer is option (a).
Q.7. Mark the correct alternatives in each of the following:
The sum of two integers is 24. If one of them is −19, then the other is
(a) 43
(b) −43
(c) 5
(d) −5
Ans: Sum of two integers = 24
One of the integers = −19
∴ Other integer = Sum of two integers − One of the integers
= 24 − (−19)
= 24 + 19
= 43
Hence, the correct answer is option (a).
Q.8. Mark the correct alternatives in each of the following:
What must be subtracted from −6 to obtain −14?
(a) 8
(b) 20
(c) −20
(d) −8
Ans: Let x be subtracted from −6 to obtain −14.
∴ −6 − x = −14
Putting x = 8, we get
LHS = −6 − 8 = −6 + (−8) = −14 = RHS
Thus, 8 must be subtracted from −6 to obtain −14.
Hence, the correct answer is option (a).
Q.9. Mark the correct alternatives in each of the following:
What should be divided by 6 to get −18?
(a) −3
(b) 3
(c) −108
(d) 108
Ans:
Let x be divided by 6 to get −18.
∴x ÷ 6 = −18
⇒x/6 = −18
Putting x = −108, we get
LHS = = RHS
= RHS
Thus, −108 should be divided by 6 to get −18.
Hence, the correct answer is (c).
Q.10. Mark the correct alternatives in each of the following:
Which of the following is correct?
(a) −12 > −9
(b) −12 < −9
(c) (−12) + 9 > 0
(d) (−12) × 9 > 0
Ans: We know that if a and b are two negative integers, then the integer with greater absolute value is less than the integer with smaller absolute value.
Absolute value of −12 = | −12 | = 12
Absolute value of −9 = | −9 | = 9
∴ −12 < −9
Also,
(−12) + 9 = −3 < 0
and (−12) × 9 = −(12 × 9) = −108 < 0
Hence, the correct answer is option (b).
Q.11. Mark the correct alternative in each of the following:
The sum of two integers is −8. If one of the integers is 12, then the other is
(a) 20
(b) 4
(c) −4
(d) −20
Ans: Sum of two integers = −8
One of the integers = 12
∴ Other integer = Sum of two integers − One of the integers
= −8 − 12
= −8 + (−12)
= −20
Hence, the correct answer is option (d).
Q.12. Mark the correct alternative in each of the following:
On subtracting −14 from −18, we get
(a) 4
(b) −4
(c) −32
(d) −32
Ans: −14 subtracted from −18
= −18 − (−14)
= −18 + 14
= −4
Hence, the correct answer is option (b).
Q.13. Mark the correct alternative in each of the following:
(−35) × 2 + (−35) × 8 =
(a) −350
(b) −70
(c) −280
(d) 350
Ans: (−35) × 2 + (−35) × 8
= (−35) × (2 + 8) [a × b + a × c = a × (b + c)]
= (−35) × 10
= −350
Hence, the correct answer is option (a).
Q.14. Mark the correct alternative in each of the following:
If x ÷ 29 = 0, then x =
(a) 29
(b) −29
(c) 0
(d) None of these
Ans: We know that if a is a non-zero integer, then 0 ÷ a = 0.
∴ x ÷ 29 = 0
⇒ x = 0
Hence, the correct answer is option (c).
Q.15. Mark the correct alternative in each of the following:
If x = (−10) + (−10) + ... 15 times and y = (−2) × (−2) × (−2) × (−2) × (−2), then x − y =
(a) 118
(b) −118
(c) −182
(d) 182
Ans: x = (−10) + (−10) + ... 15 times
= − (10 + 10 + ... 15 times)
= −150
y = (−2) × (−2) × (−2) × (−2) × (−2)
= −(2 × 2 × 2 × 2 × 2)
(When the number of negative integers in a product is odd, the product is negative)
= −32
∴ x − y = −150 − (−32) = −150 + 32 = −118
Hence, the correct answer is option (b).
Q.16. Mark the correct alternative in each of the following:
If a = (−1) × (−1) × (−1) × ... 100 times and b = (−1) × (−1) × (−1) × ... 95 times, then a + b =
(a) −1
(b) −2
(c) 0
(d) 1
Ans: a = (−1) × (−1) × (−1) × ... 100 times
Here, the number of integers in the product is even.
∴ a = (−1) × (−1) × (−1) × ... 100 times
= 1 × 1 × 1 × ... 100 times
= 1
b = (−1) × (−1) × (−1) × ... 95 times
Here, the number of integers in the product is odd.
∴ b = (−1) × (−1) × (−1) × ... 95 times
= −(1 × 1 × 1 × ... 95 times)
= −1
So,
a + b = 1 + (−1) = 0
Hence, the correct answer is option (c).
Q.17. Mark the correct alternative in each of the following:
|| 3 − 12| − 4| =
(a) −5
(b) 5
(c) 7
(d) −7
Ans:
|| 3 − 12| − 4|
= || 3 + (−12)| − 4|
= || −9| − 4|
= |9 − 4| (Absolute value of an integer is its numerical value regardless of its sign)
= |5|
= 5
Hence, the correct answer is option (b).
Q.18. Mark the correct alternative in each of the following:
If the difference of an integer a and (−9) is 5, then a =
(a) 4
(b) 5
(c) −4
(d) −9
Ans: a − (−9) = 5 (Given)
⇒ a + 9 = 5
Putting a = −4, we get
LHS = −4 + 9 = 5 = RHS
∴ a = −4
Hence, the correct answer is option (c).
Q.19. Mark the correct alternative in each of the following:
The sum of two integers is 10. If one of them is negative, then the other has to be
(a) negative (b) positive
(c) may be positive or negative (d) None of these
Ans: It is given that the sum of two integers is 10, which is a positive integer.
But, we know that the sum of two negative integers is always a negative integer.
So, if the sum of two integers is positive and one of them is negative, then the other has to be positive.
For example,
−2 + 12 = 10
−5 + 15 = 10
Thus, the other integer has to be positive.
Hence, the correct answer is option (b).
Q.20. Mark the correct alternative in each of the following:
If x = (−1) × (−1) × (−1) × (−1) × ... 25 times, y = (−3) × (−3) × (−3), then xy
(a) −27
(b) 27
(c) 26
(d) −26
Ans: x = (−1) × (−1) × (−1) × (−1) × ... 25 times
The number of integers in the given product is odd.
∴ x = (−1) × (−1) × (−1) × (−1) × ... 25 times
= −(1 × 1 × 1 × ... 25 times)
= −1
y = (−3) × (−3) × (−3)
The number of integers in the given product is odd.
∴ y = (−3) × (−3) × (−3)
= −(3 × 3 × 3)
= −27
So,
xy = (−1) × (−27) = 27 (Product of two negative integers is always positive)
Hence, the correct answer is option (b).
|
76 videos|386 docs|39 tests
|
FAQs on Integers (Exercise 1.4) RD Sharma Solutions - Mathematics (Maths) Class 7 (Old NCERT)
| 1. What are integers? |  |
| 2. How are integers represented on a number line? |  |
| 3. What is the difference between positive and negative integers? |  |
| 4. How do we perform addition and subtraction of integers? |  |
| 5. Can you give an example of multiplying and dividing integers? |  |





















