Whole Numbers (Exercise 3.1) RD Sharma Solutions | Mathematics (Maths) Class 6 PDF Download
Q.1. Write down the smallest natural number.
Ans: The smallest natural number is 1.
Q.2. Write down the smallest whole number.
Ans: The smallest whole number is 0 (zero).
Q.3. Write down, if possible, the largest natural number.
Ans: We know that every natural number has a successor. Thus, there is no largest natural number.
Q.4. Write down, if possible, the largest whole number.
Ans: We know that every whole number has a successor. Thus, there is no largest whole number.
Q.5. Are all natural numbers also whole numbers?
Ans: Yes, all natural numbers are whole numbers.
Q.6. Are all whole numbers also natural numbers?
Ans: No, all whole numbers are not natural numbers because 0 is a whole number but not a natural number.
Q.7. Give successor of each of the whole numbers?
(i) 1000909
(ii) 2340900
(iii) 7039999
Ans:
Given Number Successor
(i) 1,000,909 1,000,909 + 1 = 1,000,910
(ii) 2,340,900 2,340,900 + 1 = 2,340,901
(iii) 7,039,999 7,039,999 + 1 = 7,040,000
Q.8. Write down the predecessor of each of the following whole numbers:
(i) 10000
(ii) 807000
(iii) 7005000
Ans:
Given Number Predecessor
(i) 10,000 10,000 - 1 = 9,999
(ii) 807,000 807,000 - 1 = 806,999
(iii) 7,005,000 7,005,000 - 1 = 7,004,999
Q.9. Represent the following numbers on the number line:
2,0,3,5,7,11,15
Ans:
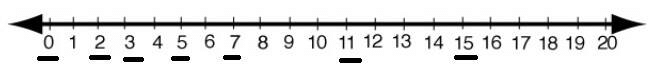
Q.10. How many whole numbers are there between 21 and 61?
Ans: The whole numbers between 21 and 61 are 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59 and 60.
Thus, there are 39 whole numbers between 21 and 61.
Q.11. Fill in the blanks with the appropriate symbol < or >:
(i) 25...205
(ii) 170...107
(iii) 415...514
(iv) 10001...100001
(v) 2300014...2300041
Ans: We have:
(i) 25 < 205
(ii) 170 > 107
(iii) 415 < 514
(iv) 10001 < 100001
(v) 2300014 < 2300041
Q.12. Arrange the following numbers is descending order:
925, 786, 1100, 141, 325, 886, 0, 270
Ans: Numbers in descending order:
1100, 925, 886, 786, 325, 270, 141, 0
Q.13. Write the largest number of 6 digits and the smallest number of 7 digits. Which one of these two is larger and by how much?
Ans:
Largest six-digit number = 999,999
Smallest seven-digit number = 1,000,000
Thus, the smallest seven-digit number is larger than the largest six-digit number.
Again,
Difference between these two numbers = 1,000,000 - 999,999 = 1
Hence, the smallest seven-digit number is larger than the largest six-digit number by 1.
Q.14. Write down three consecutive whole numbers just preceding 8510001.
Ans: We have:
First number = 8,510,001 - 1 = 8,510,000
Second number = 8,510,000 - 1 = 8,509,999
Third number = 8,509,999 - 1 = 8,509,998
Hence, the three consecutive whole numbers just preceding 8,510,001 are 8,510,000, 8,509,999 and 85,09,998.
Q.15. Write down the next three consecutive whole numbers starting from 4009998.
Ans: We have:
First number = 4,009,998 + 1 = 4,009,999
Second number = 4,009,999 + 1 = 4,010,000
Third number = 4,010,000 + 1 = 4,010,001
Hence, the next three consecutive whole numbers starting from 4,009,998 will be 4,009,999, 4,010,000 and 4,010,001.
Q.16. Give arguments in support of the statement that there does not exist the largest natural number.
Ans: We know that every natural number has a successor. Therefore, the largest natural number does not exist.
Q.17. Which of the following statements are true and which are false?
(i) Every whole number has its successor.
(ii) Every whole number has its predecessor.
(iii) 0 is the smallest natural number.
(iv) 1 is the smallest whole number.
(v) 0 is less than every natural number.
(vi) Between any two whole numbers there is a whole number.
(vii) Between any two non-consecutive whole numbers there is a whole number.
(viii) The smallest 5-digit number is the successor of the largest 4 digit number
(ix) Of the given two natural numbers, the one having more digits is greater.
(x) The predecessor of a two digit number cannot be a single digit number.
(xi) If a and b are natural numbers and a < b, than there is a natural number c such that a<b<c.
(xii) If a and b are whole numbers and a<b, then a+1< b+1.
(xiii) The whole number 1 has 0 as predecessor.
(xiv) The natural number 1 has no predecessor.
Ans:
(i) True
The successor of every whole number can be found by adding 1.
(ii) False
Zero (0) is a whole number whose predecessor (-1) is not a whole number.
(iii) False
1 is the smallest natural number.
(iv) False
Zero (0) is the smallest whole number.
(v) True
The smallest natural number is 1, so zero (0) is less than every natural number.
(vi) False
There is no whole number between two consecutive whole numbers.
(vii) True
(viii) True
The smallest five-digit number = 10,000
The largest four-digit number = 9,999
Difference = 10,000 - 9,999 = 1
Because the difference is 1, 10,000 is the successor of 9,999.
(ix) True
(x) False
10 is a two-digit number whose predecessor is 9, which is a one-digit number.
(xi) False
If a and b are consecutive natural numbers, then there cannot be any natural number c in between a and b.
(xii) True
(xiii) True
(xiv) True
The predecessor of natural number 1 is 0, which is not a natural number.
Objective Type Questions
Q.1. The smallest natural number is
(a) 0
(b) 1
(c) -1
(d) None of these
Ans: (b) 1
Q.2. The smallest whole number is
(a) 1
(b) 0
(c) -1
(d) None of these
Ans: (b) 0
Q.3. The predecessor of 1 in natural numbers is
(a) 0
(b) 2
(c) -1
(d) None of these
Ans: (d) None of these
We know that the smallest natural number is 1. Hence, its predecessor does not exist.
Q.4. The predecessor of 1 in whole numbers is
(a) 0
(b) -1
(c) 2
(d) None of these
Ans: (a) 0
Predecessor of 1 = 1 - 1 = 0
Q.5. The predecessor of 1 million is
(a) 9999
(b) 99999
(c) 999999
(d) 1000001
Ans: (c) 9,99,999
We have:
1 million = 10,00,000
Predecessor of 1 million
= 10,00,000 - 1
= 9,99,999
Q.6. The successor of 1 million is
(a) 10001
(b) 100001
(c) 1000001
(d) 10000001
Ans: (c) 10,00,001
We have:
1 million = 10,00,000
Successor of 1 million
= 10,00,000 + 1
= 10,00,001
Q.7. The product of the successor and predecessor of 99 is
(a) 9800
(b) 9900
(c) 1099
(d) 9700
Ans: (a) 9800
We have:
Successor of 99 = 99 + 1 = 100
Predecessor of 99 = 99 − 1 = 98
Their product = 100 × 98 = 9800
Q.8. The product of a whole number (other than zero) and its successor is
(a) an even number
(b) an odd number
(c) divisible by 4
(d) divisible by 3
Ans: (a) an even number
Example:
Whole number = 1
Successor of 1 = 1 + 1 = 2
Their product = 1 × 2 = 2
Thus, 2 is an even number.
Q.9. The product of the predecessor and successor of an odd natural number is always divisible by
(a) 2
(b) 4
(c) 6
(d) 8
Ans: (d) 8
The predecessor of an odd number is an even number.
The successor of an odd number is also an even number.
These two even numbers are two consecutive even numbers, and the product of two consecutive even numbers is always divisible by 8.
Q.10. The product of the predecessor and successor of an even natural number is
(a) divisible by 2
(b) divisible by 3
(c) divisible by 4
(d) an odd number
Ans: (d) an odd number
Example:
Even natural number = 2
Predecessor of 2 = 2 − 1 = 1
Successor of 2 = 2 + 1 = 3
Their product = 1 × 3 = 3
Thus, the product is an odd number.
Q.11. The successor of the smallest prime number is
(a) 1
(b) 2
(c) 3
(d) 4
Ans: The smallest prime number is 2
So, Successor of 2 = 2 + 1 = 3
Hence, the correct answer is option (c).
Q.12. If x and y are co-primes, then their LCM is
(a) 1
(b) x/y
(c) xy
(d) None of these
Ans: A set of numbers which do not have any other common factor other than 1 are called co-prime.
The LCM of two co-prime numbers is equal to their product.
Hence, the correct answer is option (c).
Q.13. The HCF of two co-primes is
(a) the smaller number
(b) the larger number
(c) product of the numbers
(d) 1
Ans: A set of numbers which do not have any other common factor other than 1 are called co-prime.
The HCF of two co-prime numbers is 1.
Hence, the correct answer is option (d).
Q.14. The smallest number which is neither prime nor composite is
(a) 0
(b) 1
(c) 2
(d) 3
Ans: The smallest number which is neither prime nor composite is 1
Hence, the correct answer is option (b).
Q.15. The product of any natural number and the smallest prime is
(a) an even number
(b) an odd number
(c) a prime number
(d) None of these
Ans: The smallest prime number is 2.
Thus, when we multiply any natural number we will always get an even number.
Hence, the correct answer is option (a).
Q.16. Every counting number has an infinite number of
(a) factors
(b) multiples
(c) prime factors
(d) None of these
Ans: Multiples are what we get after multiplying the number by any number.
Thus, every counting number has an infinite number of multiples
Hence, the correct answer is option (b).
Q.17. The product of two numbers is 1530 and their HCF is 15. The LCM of these numbers is
(a) 102
(b) 120
(c) 84
(d) 112
Ans:
Product of two numbers = HCF of two numbers × LCM of two numbers
⇒1530=15×LCM of two numbers
⇒LCM of two numbers=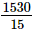 = 102
= 102
Hence, the correct answer is option (a).
Q.18. The least number divisible by each of the numbers 15, 20, 24 and 32 is
(a) 960
(b) 480
(c) 360
(d) 640
Ans: LCM of 15, 20, 24 and 32 is given by
15 = 3 × 5 = 31 × 51
20 = 2 × 2 × 5 = 22 × 51
24 = 2 × 2 × 2 × 3 = 23 × 31
32 = 2 × 2 × 2 × 2 × 2 = 25
LCM = 25 × 31 × 51 = 480
Hence, the correct answer is option (b).
Q.19. The greatest number which divides 134 and 167 leaving 2 as remainder in each case is
(a) 14
(b) 19
(c) 33
(d) 17
Ans: First we subtract the required remainder from 134 and 167.
Thus, we will get 132 and 165.
132 = 2 × 2 × 3 × 11 = 22 × 3 × 11
165 = 3 × 5 × 11 = 31 × 5 × 11
HCF = 3 × 11 = 33
Thus, the greatest number which divides 134 and 167 leaving 2 as remainder in each case is 33
Hence, the correct answer is option (c).
Q.20. Which of the following numbers is a prime number?
(a) 91
(b) 81
(c) 87
(d) 97
Ans: Since, factors of
91 = 1 × 7 × 13
81 = 1 × 3 × 3 × 3 × 3
87 = 1 × 3 × 29
97 = 1 × 97
Thus, 81, 87 and 91 all are not prime numbers.
Hence, the correct answer is option (d).
Q.21. If two numbers are equal, then
(a) their LCM is equal to their HCF
(b) their LCM is less than their HCF
(c) their LCM is equal to two times their HCF
(d) None of these
Ans: If two numbers are equal, then their LCM is equal to their HCF
Hence, the correct answer is option (a).
Q.22. a and b are two co-primes. Which of the following is/are true?
(a) LCM (a, b) = a × b
(b) HCF (a, b) = 1
(c) Both (a) and (b)
(d) Neither (a) nor (b)
Ans: A set of numbers which do not have any other common factor other than 1 are called co-prime.
The LCM of two co-prime numbers is equal to their product.
The HCF of two co-prime numbers is 1.
Hence, the correct answer is option (c).
|
92 videos|348 docs|54 tests
|
FAQs on Whole Numbers (Exercise 3.1) RD Sharma Solutions - Mathematics (Maths) Class 6
| 1. What is the importance of whole numbers in mathematics? |  |
| 2. How can whole numbers be classified? |  |
| 3. Can whole numbers be negative? |  |
| 4. What are the properties of whole numbers? |  |
| 5. How are whole numbers used in real-life situations? |  |

|
Explore Courses for Class 6 exam
|

|

















