Playing With Numbers (Exercise 2.11) RD Sharma Solutions | Mathematics (Maths) Class 6 PDF Download
Q.1. For each of the following pairs of numbers, verify the property:
Product of the number = Product of their H.C.F and L.C.M
(i) 25,65
(ii) 117,221
(iii) 35,40
(iv) 87,145
(v) 490,1155
Ans:
(i) Given numbers are 25 and 65.
Prime factorisation of 25 = 5 × 5
Prime factorisation of 65 = 5 × 13
HCF of 25 and 65 = 5
LCM of 25 and 65 = 5 × 5 × 13 = 325
Product of the given numbers = 25 × 65 = 1,625
Product of their HCF and LCM = 5 × 325 = 1,625
∴ Product of the number = Product of their HCF and LCM (Verified)
(ii) Given numbers are 117 and 221.
Prime factorisation of 117 = 3 × 3 × 13
Prime factorisation of 221 = 13 × 17
HCF of 117 and 221 = 13
LCM of 117 and 221 = 3 × 3 × 13 × 17 = 1,989
Product of the given number = 117 × 221 = 12,857
Product of their HCF and LCM = 13 × 1,989 = 12,857
∴ Product of the number = Product of their HCF and LCM (Verified)
(iii) Given numbers are 35 and 40.
Prime factorisation of 35 = 5 × 7
Prime factorisation of 40 = 2 × 2 × 2 × 5
HCF of 35 and 40 = 5
LCM of 35 and 40 = 2 × 2 × 2 × 5 × 7 = 280
Product of the given number = 35 × 40 = 1,400
Product of their HCF and LCM = 5 × 280 = 1,400
∴ Product of the number = Product of their HCF and LCM (Verified)
(iv) Given numbers are 87 and 145.
Prime factorisation of 87 = 3 × 29
Prime factorisation of 145 = 5 × 29
HCF of 87 and 145 = 29
LCM of 87 and 145 = 3 × 5 × 29 = 435
Product of the given number = 87 × 145 = 12,615
Product of their HCF and LCM = 29 × 435 = 12,615
∴ Product of the number = Product of their HCF and LCM (Verified)
(v) Given numbers are 490 and 1,155.
Prime factorisation of 490 = 2 × 5 × 7 × 7
Prime factorisation of 1,155 = 3 × 5 × 7 × 11
HCF of 490 and 1,155 = 5 × 7 = 35
LCM of 490 and 1,155 = 2 × 3 × 3 × 5 × 7 × 7 × 11 = 16,170
Product of the given number = 490 × 1,155 = 5,65,950
Product of their HCF and LCM = 35 × 16,170 = 5,65,950
∴ Product of the number = Product of their HCF and LCM (Verified)
Q.2. Find the H.C.F and L.C.F of the following pairs of numbers:
(i) 117,221
(ii) 234,572
(iii) 145,232
(iv) 861,1353
Ans:
(i) 117 and 221
Prime factorisation of 117 = 3 × 3 × 13
Prime factorisation of 221 = 13 × 17
∴ Required HCF of 117 and 221 = 13
∴ Required LCM of 117 and 221 = 3 × 3 × 13 × 17 = 1,989
(ii) 234 and 572
Prime factorisation of 234 = 2 × 3 × 3 × 13
Prime factorisation of 572 = 2 × 2 × 11 × 13
Required HCF of 234 and 572 = 2 × 13 = 26
Required LCM of 234 and 572 = 2 × 2 × 3 × 3 × 11 × 13 = 5,148
(iii) 145 and 232
Prime factorisation of 145 = 5 × 29
Prime factorisation of 232 = 2 × 2 × 2 × 29
Required HCF of 145 and 232 = 29
Required LCM of 145 and 232 = 2 × 2 × 2 × 5 × 29 = 1,160
(iv) 861 and 1,353
Prime factorisation of 861 = 3 × 7 × 41
Prime factorisation of 1,353 = 3 × 11 × 41
Required HCF of 861 and 1,353 = 3 × 41 = 123
Required LCM of 861 and 1,353 = 3 × 7 × 11 × 41 = 9,471
Q.3. The L.C.M and H.C.F of two numbers are 180 and 6 respectively. If ones of the numbers is 30, find the other number.
Ans: Given:
HCF of two numbers = 6
LCM of two numbers = 180
One of the given number = 30
Product of the two numbers = Product of their HCF and LCM
∴ 30 × other number = 6 × 180
Other number =6×180/30 = 36
Thus, the required number is 36.
Q.4. The H.C.F of two numbers is 16 and their product is 3072. Find their L.C.M.
Ans: Given:
HCF of two numbers = 16
Product of these two numbers = 3,072
Product of the two numbers = Product of their HCF and LCM
∴ 3,072 = 16 × LCM
LCM = =3072/16 = 192
Thus, the required LCM is 192.
Q.5. The H.C.F of two numbers is 145, their L.C.M is 2175. If one number is 725, find the other.
Ans:
HCF of two numbers = 145
LCM of two numbers = 2,175
One of the given numbers = 725
Product of the given two numbers = Product of their LCM and HCF
∴ 725 × other number = 145 × 2,175
Other number = 145 x 2175/725 =435
Thus, the required number is 435.
Q.6. Can two numbers have 16 as their H.C.F and 380 as their L.C.M.? Give reason.
Ans: No.
We know that HCF of the given two numbers must exactly divide their LCM.
But 16 does not divide 380 exactly.
Hence, there can be no two numbers with 16 as their HCF and 380 as their LCM.
Objective Type Questions
Q.1. Which of the following numbers is a perfect number?
(a) 4
(b) 12
(c) 8
(d) 6
Ans: (d) 6
A number for which the sum of all its factors is equal to twice the number is called a perfect number.
Factors of 6 are 1, 2 ,3, and 6.
Sum of the factors of 6 = 1 + 2 + 3 + 6 = 12 = 2 × 6
Hence, 6 is a perfect number.
Q.2. Which of the following are not twin-primes?
(a) 3,5
(b) 5,7
(c) 11,13
(d) 17,23
Ans: (d) 17, 23
Pairs of prime numbers that differ by 2 are called twin primes.
The difference between 17 and 23 is 6.
Hence, 17 and 23 are not twin primes.
Q.3. Which of the following are co-primes?
(a) 8,10
(b) 9,10
(c) 6,8
(d) 15,18
Ans: (b) 9, 10
9 = 3 ×3 × 1
10 = 2 × 5 × 1
Though both 9 and 10 are composite numbers, the only factor common to them is 1.
Therefore, 9 and 10 are co-primes.
Q.4. Which of the following is a prime number?
(a) 263
(b) 361
(c) 323
(d) 324
Ans: (a) 263
263 = 1 × 263
The number 263 has only two factors, 1 and 263.
Hence, it is a prime number.
Q.5. The number of primes between 90 and 100 is
(a) 0
(b) 1
(c) 2
(d) 3
Ans: (b) 1
There is only one prime number between 90 and 100, i.e. 97.
Q.6. Which of the following numbers is a perfect number?
(a) 16
(b) 8
(c) 24
(d) 28
Ans: (d) 28
A number for which the sum of all its factors is equal to twice the number is called a perfect number.
Factors of 28 are 1, 2 , 4, 7, 14, and 28.
Sum of factors of 28 = 1 + 2 + 4 + 7 + 14 + 28 = 56 = 2 × 28
Hence, 28 is a perfect number.
Q.7. Which of the following is a prime number?
(a) 203
(b) 139
(c) 115
(d) 161
Ans: (b) 139
139 = 1 × 139
The number 139 has only two factors, 1 and 139.
Hence, it is a prime number.\
Q.8. The total number of even prime numbers is
(a) 0
(b) 1
(c) 2
(d) unlimited
Ans: (b) 1
There is only one even number that is prime, i.e. 2.
Q.9. Which one of the following is a prime number?
(a) 161
(b) 221
(c) 373
(d) 437
Ans: (c) 373
373 = 1 × 373
The number 373 has only two factors, 1 and 373.
Hence, it is a prime number.
Q.10. The least prime is
(a) 1
(b) 2
(c) 3
(d) 5
Ans: (b) 2
2 is the least prime number. It is the only even prime number.
Q.11. Which one of the following numbers is divisible by 3?
(a) 27326
(b) 42356
(c) 73545
(d) 45326
Ans: (c) 73,545
Sum of the digits in 73,545 = 7 + 3 + 5 + 4 + 5 = 24
Since 24 is divisible by 3, 73545 is divisible by 3.
Q.12. Which of the following numbers is divisible by 4?
(a) 8675231
(b) 9843212
(c) 1234567
(d) 543123
Ans: (b) 98,43,212
Here, the number formed by the last two digits is 12, which is divisible by 4.
Therefore, 98,43,212 is divisible by 4.
Q.13. Which of the following numbers is divisible by 6?
(a) 7908432
(b) 68719402
(c) 45982024
(d) 24567891
Ans: A number divisible by 6 must also be divisible by 3 and 2 as 6 is a multiple of 3 and 2.
In 79,08,432, the sum of the digits = 7 + 9 + 0 + 8 + 4 + 3 + 2 = 33
Since 33 is a multiple of 3, this number is divisible by 3.
Also, since the last digit is 2, it is also divisible by 2.
Therefore, 79,08,432 is divisible by 6.
Hence the correct answer is option (a).
Q.14. Which of the following numbers is divisible by 8?
(a) 87653234
(b) 78956042
(c) 64298602
(d) 98741032
Ans: (d) 9,87,41,032
In 9,87,41,032, the number formed by the last three digits is 032, which is also divisible by 8.
Hence, 9,87,41,032 is divisible by 8.
Q.15. Which of the following numbers is divisible by 9?
(a) 9076185
(b) 92106345
(c) 10349576
(d) 95103476
Ans: (a) 90,76,185
In 90,76,185:
Sum of the digits = 9 + 0 + 7 + 6 + 1 + 8 + 5 = 36
Since 36 is divisible by 9, 9076185 is divisible by 9.
Q.16. Which of the following numbers is divisible by 11?
(a) 1111111
(b) 22222222
(c) 3333333
(d) 4444444
Ans: (b) 2,22,22,222
In 2,22,22,222, the difference of the sum of alternate digits 2 + 2 + 2 + 2 = 8 and 2 + 2 + 2 +2 = 8 is zero.
Hence, the number is divisible by 11.
Q.17. If 1*548 is divisible by 3, then * can take the value
(a) 0
(b) 2
(c) 7
(d) 8
Ans: (a) 0
Sum of the given digits = 1 + 5 + 4 + 8 = 18
Since 18 is a multiple of 3, the required digit is 0.
Q.18. 5*2 is a three digit number with * as a missing digit. If the number is divisible by 6, the missing digit is.
(a) 2
(b) 3
(c) 6
(d) 7
Ans: (a) 2
A number divisible by 6 must also be divisible by 3 as 6 is a multiple of 3.
Sum of the given digits = 5 + 2 = 7
We know that multiple of 3 greater than 7 is 9.
∴ 9 − 7 = 2
Therefore, the required digit is 2.
Q.19. What least value should be given to * so that the number 6342*1 is divisible by 3?
(a) 0
(b) 1
(c) 2
(d) 3
Ans: (c) 2
Sum of the given digits = 6 + 3 + 4 + 2 + 1 = 16
We know that multiple of 3 greater than 16 is 18.
∴ 18 − 16 = 2
Therefore, the smallest required digit is 2.
Q.20. What least value should be given to * so that the number 915*26 is divisible by 9?
(a) 1
(b) 4
(c) 2
(d) 6
Ans: (b) 4
A number is divisible by 9 if the sum of its digits is a multiple of 9.
Sum of the given digits = 9 + 1 + 5 + 2 + 6 = 23
We know that multiple of 9 greater than 23 is 27.
∴ 27 − 23 = 4
Hence, the smallest required digit is 4.
Q.21. What least number be assigned to * so that number 653*47 is divisible by 11?
(a) 1
(b) 2
(c) 6
(d) 9
Ans: (a) 1
Sum of the digits at odd places = 6 + 3 + 4 = 13
Sum of the digits at even places = 5 + * + 7 = 12 + *
Difference = 13 − [12 + *] = 1 − *
If 6,53,*47 is divisible by 11, then 1 − * must be zero or multiple of 11.
1 − * = 0 or 11
* = 1 or −10
But * is a digit, so * must be 1.
Q.22. What least number be assigned to * so that the number 63576*2 is divisible by 8?
(a) 1
(b) 2
(c) 3
(d) 4
Ans: (c) 3
The given number is divisible by 8 if the number formed by its last three digits is divisible by 8.
Hence, 63,57,6*2 is divisible by 8 if 6*2 is divisible by 8.
Thus, the least value of * will be 3.
Q.23. Which one of the following numbers is exactly divisible by 11?
(a) 235641
(b) 245642
(c) 315624
(d) 415624
Ans: (d) 4,15,624
Sum of digits at odd places = 4 + 5 + 2 = 11
Sum of digits at even places = 1 + 6 + 4 = 11
Difference of these two sums = 11 − 11 = 0
Therefore, 4,15,624 is divisible by 11.
Q.24. If 1*548 is divisible by 3, which of the following digits can replace *?
(a) 0
(b) 2
(c) 7
(d) 9
Ans: (a) 0
Sum of the given digits = 1 + 5 + 4 + 8 = 18
Since 18 is a multiple of 3, the required digit is 0.
Q.25. The sum of the prime numbers between 60 and 75 is
(a) 199
(b) 201
(c) 211
(d) 272
Ans: (d) 272
Prime numbers between 60 and 75 are 61, 67, 71, and 73.
Their sum is given by:
61 + 67 + 71 + 73 = 272
Q.26. The HCF of two consecutive natural numbers is
(a) 0
(b) 1
(c) 2
(d) non-existant
Ans: (b) 1
The HCF of any two consecutive natural numbers is 1 because two consecutive natural numbers are always co-prime.
Q.27. The HCF of two consecutive even numbers is
(a) 1
(b) 2
(c) 0
(d) non-existant
Ans: (b) 2
HCF of two consecutive even numbers is always 2.
For example:
HCF of 4 and 6 is 2.
HCF of 10 and 12 is 2 and so on.
Q.28. The HCF of two consecutive odd numbers is
(a) 1
(b) 2
(c) 0
(d) non-existant
Ans: (a) 1
We know that the common factor of two consecutive odd numbers is 1.
Thus, HCF of two consecutive odd numbers is 1.
Q.29. The HCF of an even number and an odd number is
(a) 1
(b) 2
(c) 0
(d) non-existant
Ans: (d) non-existent
Example: HCF of 8 and 21 is 1.
HCF of 6 and 9 is 3.
HCF of 9 and 36 is 9.
So there is no fixed number that can be the HCF of an even number and an odd number.
Q.30. The LCM of 24,36 and 40 is
(a) 4
(b) 90
(c) 360
(d) 720
Ans: (c) 360
We have:
24 = 2 × 2 × 2 × 3 = 23 × 3
36 = 2 × 2 × 3 × 3 = 22 × 32
40 = 2 × 2 × 2 × 5 = 23 × 5
Here, 2, 3, and 5 are the prime factors. Highest powers of 2, 3, and 5 are 3, 2, and 1, respectively.
∴ LCM of 24, 36, and 40 = 23 × 32 × 5 = 8 × 9 × 5 = 360
Q.31. If x and y are two co-primes, then their LCM is
(a) xy
(b) x+y
(c) x/y
(d) 1
Ans: (a) xy
The LCM of two co-prime numbers is equal to their product.
Thus, LCM of 'x' and 'y' will be xy.
Q.32. If the HCF of two number is 16 and their product is 3072, then their LCM is
(a) 182
(b) 192
(c) 12
(d) None of these
Ans: (b) 192
We know:
HCF × LCM = Product of two numbers
∵ 16 × LCM = 3,072
∴ LCM = 3,072/16=192
Q.33. The least number divisible by 15,20,24,32 and 36 is
(a) 1440
(b) 1660
(c) 2880
(d) None of these
Ans: (a) 1,440
The least number divisible by 15, 20, 24, 32, and 36 can be found by taking their LCM as:
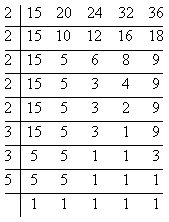
∴ LCM of 15, 20, 24, 32 and 36 = 2 × 2 × 2 × 2 × 2 × 3 × 3 × 5 = 1,440
Hence, 1,440 is the least number that is divisible by 15, 20, 24, 32 and 36.
Q.34. The smallest number which when diminished by 3 is divisible by 21, 28, 36 and 45 is
(a) 1257
(b) 1260
(c) 1263
(d) None of these
Ans: Required smallest number = LCM of (21, 28, 36, 45) + 3 = 1260 + 3 = 1263
Hence, the correct answer is option (c).
Q.35. Three numbers are in the ratio 1:2:3 and their HCF is 6, the numbers are
(a) 4,8,12
(b) 5,10,15
(c) 6,12,18
(d) 10,20,30
Ans: (c) 6, 12, 18
Three numbers are 1× HCF, 2 × HCF, and 3 × HCF, i.e. 1 × 6 = 6, 2 × 6 = 12, and 3 × 6 = 18.
Thus, the numbers are 6, 12, 18.
Q.36. The ratio of two numbers is 3:4 and their HCF is 4. Their LCM is
(a) 12
(b) 16
(c) 24
(d) 48
Ans: (d) 48
Two numbers are 3 × HCF and 4 × HCF
i.e. 3 × 4 = 12 and 4 × 4 = 16
LCM of 12 and 16 = 48
CCE Chapter Test - 1
Q.1. Which of the following numbers is prime?
(a) 23
(b) 51
(c) 38
(d) 26
Ans:
(a) 23 = 1 × 23,
23 has only two factors 1 and 23, Therfore, it is a prime number.
(b) 51 = 1 × 3 × 17,
51 has three factors 1, 3 and 17, Therfore, it is a composite number.
(c) 38 = 1 × 2 × 19,
38 has three factors 1, 2 and 19, Therfore, it is a composite number.
(d) 26 = 1 × 2 × 13,
26 has three factors 1, 2 and 13, Therfore, it is a composite number.
Hence, the correct answer is option (a).
Q.2. Which of the following numbers are twin primes?
(a) 3,5
(b) 5,11
(c) 3,11
(d) 13,17
Ans: Twin primes are pairs of primes which differ by two.
In (3, 5), the difference between the two primes is 2.
Therefore, (3, 5) are twin primes.
Hence, the correct answer is option (a).
Q.3. What smallest digit be written in the blank space of the mumber ......6724 so that the number formed is divisible by 3?
(a) 3
(b) 4
(c) 2
(d) 1
Ans: A number is divisible by 3 if the sum of its digits is divisible by 3.
The sum of digits in 6724 is 6 + 7+ 2 + 4 = 19
For divisble by 3 we have to add 2 in 19 i.e., 2 + 19 = 21, which is divisible by 3.
Hence, the correct answer is option (c).
Q.4. Which of the following numbers is divisible by 6?
(a) 1258
(b) 61233
(c) 901352
(d) 1790184
Ans: A number divisible by 2 and 3 is also divisble by 6.
Since, 1790184 is an even number
Therefore, it is divisible by 2.
The sum of digits in 1790184 is 1 + 7 + 9 + 0 + 1 + 8 + 4 = 30, which is divisible by 3.
Therefore, 1790184 is divisible by 6.
Hence, the correct answer is option (d).
Q.5. Which of the following numbers is divisible by 11?
(a) 7138965
(b) 10000001
(c) 10834
(d) 901154
Ans: A number is divisible by 11 if the difference of the sums of alternating digits is divisible by 11.
Sum of the digits at odd places = 1 + 0 + 0 + 0 = 1
Sum of the digits at even places = 0 + 0 + 0 + 1 = 1
Required difference, 1 − 1 = 0
Since, 0 is divisible by 11.
Therefore, 10000001 is divisible by 11.
Hence, the correct answer is option (b).
Q.6. Which of the following numbers is a perfect number?
(a) 12
(b) 28
(c) 8
(d) 16
Ans: A perfect number is a positive number that equals the sum of its divisors, excluding itself.
Divisors of 12 = 1, 2, 3 ,4 ,6 ,12
Divisors of 28 = 1, 2, 4, 7, 14, 28
Divisors of 8 = 1, 2 ,4 ,8
Divisors of 16 = 1, 2 ,4 ,8 ,16
In 28, the sum of divisors except itself, 1 + 2 + 4 + 7 + 14 is 28.
Hence, the correct answer is option (b).
Q.7. Which of the folowing numbers is not divisible by 4?
(a) 78536
(b) 1264
(c) 6421
(d) 7935
Ans: A number is divisible by 4 if the number's last two digits are divisible by 4.
In (a) 78536 and (b) 1264, the last two digits 36 and 64 respectively are divisible by 4.
Therefore, (a) 78536 and (b) 1264 are divisible by 4.
In (c) 6421 and (d) 7935 the last two digits 21 and 35 respectively are not divisible by 4.
Therefore, (c) 6421 and (d) 7935 are not divisible by 4.
Q.8. The smallest prime just greater than the HCF of 84 and 144 is
(a) 11
(b) 17
(c) 19
(d) 13
Ans: 84 = 1 × 2 × 2 × 3 × 7 = 22 × 31 × 71
144 = 1 ×2 × 2 × 2 × 2 × 3 × 3 = 24 × 32
HCF of 84 and 144 = 22 × 31 = 12
Prime number just greater than 12 is 13.
Hence, the correct answer is option (d).
Q.9. Every counting number has an infinite number of
(a) factors
(b) multiples
(c) prime factors
(d) None of these
Ans: Multiples are what we get after multiplying the number by any number.
Thus, every counting number has an infinite number of multiples
Hence, the correct answer is option (b).
Q.10. What least number should be replaced by * so that the number 37610*2 is exactly divisible by 9 ?
(a) 8
(b) 7
(c) 6
(d) 5
Ans: A number is divisible by 9 if the sum of its digits is divisible by 9.
The sum of digits in 37610*2 is 3 + 7+ 6 + 1 + 0 + 2 = 19
For divisble by 9 we have to add 8 in 19 i.e., 8 + 19 = 27, which is divisible by 9.
Hence, the correct answer is option (a).
Q.11. Define a perfect number. Write two perfect numbers
Ans: A perfect number is a positive number that equals the sum of its divisors, excluding itself.
Divisors of 6 = 1, 2, 3
Divisors of 28 = 1, 2, 4, 7, 14, 28
In 6, the sum of divisors except itself, 1 + 2 + 3 is 6.
In 28, the sum of divisors except itself, 1 + 2 + 4 + 7 + 14 is 28.
Two perfect numbers are 6 and 28.
Q.12. Make a list of seven consecutive numbers, none of which is prime.
Ans: The seven consecutive numbers, none of which is prime are:
90, 91, 92, 93, 94, 95, 96
Q.13. The HCF of two numbers is 23 and their product is 55545. Find their LCM
Ans: Product of two numbers = HCF of two numbers × LCM of two numbers
⇒ 55545 = 23 × LCM of two numbers
⇒ LCM of two numbers = 55545/23 = 2415
Q.14. Find the smallest 5-digit number which is exactly divisible by 20, 25, 30.
Ans:
20 = 1 × 2 × 2 × 5 = 22 × 51
25 = 1 × 5 × 5 × 31 = 52
30 = 1 × 2 × 3 × 5 = 21 × 31 × 51
LCM of 20, 25 and 30 = 22 × 31 × 52 = 300
Smallest five digit number is 10000
Now, if we divide 10000 by 60, we will get 33.33 as quotient.
The integer just greater than 33.33 is 34
∴ Required number = 300 × 34 = 10200
Hence, the smallest 5-digit number which is exactly divisible by 20, 25, 30 is 10200.
Q.15. Find the greatest number which divides 615 and 963, leaving the remainder 6 in each case.
Ans: First we subtract the required remainder from 615 and 963.
Thus, we will get 609 and 957.
609 = 3 × 7 × 29 = 31 × 71 × 291
165 = 3 × 11 × 29 = 31 × 111 × 291
HCF = 31 × 291 = 87
Hence, the greatest number which divides 615 and 963, leaving the remainder 6 in each case is 87.
Q.16. The length, breadth and height of a room are 1050 cm, 750 cm and 425 cm respectively. Find the length of the longest tape which can measure the three dimensions of the room exactly
Ans:
1050 = 1 × 2 × 3 × 5 × 5 × 7 = 21 × 31 × 52 × 71
750 = 1 × 2 × 3 × 5 × 5 × 5 = 21 × 31 × 53
425 = 1 × 5 × 5 × 17 = 52 × 171
30 = 1 × 2 × 3 × 5 = 21 × 31 × 51
HCF of 1050, 750, and 425 = 52 = 25
Hence, the length of the longest tape which can measure the three dimensions of the room exactly is 25 cm
Q.17. Find the greatest number of four digits which is exactly divisible by each of 8, 12, 18 and 30.
Ans:
8 = 1 × 2 × 2 × 2 = 23
12 = 1 × 2 × 2 × 3 = 22 × 31
18 = 1 × 2 × 3 × 3 = 21 × 32
30 = 1 × 2 × 3 × 5 = 21 × 31 × 51
LCM of 8, 12, 18, and 30 = 23 × 32 × 51 = 360
Largest 4-digit number is 9999
Now, if we divide 9999 by 360, we will get 27.78 as quotient.
The integer just less than 27.78 is 27
∴ Required number = 360 × 27 = 9720
Hence, the greatest number of four digits which is exactly divisible by each of 8, 12, 18 and 30 is 9720.
Q.18. Find the least number of five digits which is exactly divisible by each of 8, 12, 18, 40 and 45
Ans:
8 = 1 × 2 × 2 × 2 = 23
12 = 1 × 2 × 2 × 3 = 22 × 31
18 = 1 × 2 × 3 × 3 = 21 × 32
40 = 1 × 2 × 2 × 2 × 5 = 23 × 51
45 = 1 × 3 × 3 × 5 = 32 × 51
LCM of 8, 12, 18, 40 and 45 = 23 × 32 × 51 = 360
Smallest five digit number is 10000
Now, if we divide 10000 by 360, we will get 27.78 as quotient.
The integer just greater than 27.78 is 28
∴ Required number = 360 × 28 = 10080
Hence, the least number of five digits which is exactly divisible by each of 8, 12, 18, 40 and 45 is 10080.
Q.19. Reduce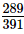 to the lowest terms
to the lowest terms
Ans:
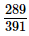 =
=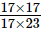
=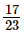
Q.20. Three tankers contain 403 lltres, 434 litres and 465 litres of diesel respectively. Find the maximum capacity of a container that can measure the diesel of three containers exact number of times.
Ans: The maximum capacity of three containers is equal to the HCF of 403, 434 and 465.
403 = 1 × 13 × 31 = 131 × 311
434 = 1 × 2 × 7 × 31 = 21 × 71 × 311
465 = 1 × 3 × 5 × 31 = 31 × 51 × 311
HCF of 403, 434 and 465 = 311 = 31
Hence, the maximum capacity of a container that can measure the diesel of three containers exact number of times is 31 litres
Q.21. A number which has only two factors is called a ..............
Ans: A number which has only two factors is called a prime number
Q.22. The smallest composite number is ......
Ans: A composite number is a positive integer which is not prime (i.e., which has factors other than 1 and itself).
Since, the factors of 4 are 1, 2 ,4.
Hence, the smallest composite number is 4.
Q.23. Two perfect numbers are ......... and ...........
Ans: A perfect number is a positive number that equals the sum of its divisors, excluding itself.
Divisors of 6 = 1, 2, 3
Divisors of 28 = 1, 2, 4, 7, 14, 28
In 6, the sum of divisors except itself, 1 + 2 + 3 is 6.
In 28, the sum of divisors except itself, 1 + 2 + 4 + 7 + 14 is 28.
Therefore, two perfect numbers are 6 and 28.
Q.24. The HCF of two consecutive odd numbers is ..........
Ans: Since, the common factor in two consecutive odd numbers is only 1.
Hence, the HCF of two consecutive odd numbers is 1.
Q.25. The prime triplet is ................
Ans: A set of three prime numbers which form an arithmetic sequence with common difference two is called a prime triplet.
Since, 3, 5 and 7 are satisfying the above condition.
Hence, the prime triplet is (3, 5, 7).
CCE Chapter Test - 2
Q.1. The greatest five digit number exactly divisible by 9 and 13 is
(a) 99945
(b) 99918
(c) 99964
(d) 99972
Ans: LCM of 9 and 13 = 9 × 13 = 117
Largest 5-digit number is 99999
Now, if we divide 99999 by 117, we will get 854.69 as quotient.
The integer just less than 854.69 is 854
∴ Required number = 117 × 854 = 99918
Hence, the correct answer is option (b).
Q.2. From the numbers 2, 3, 4, 5, 6, 7, 8, 9 how many pairs of co-primes can be formed?
(a) 19
(b) 18
(c) 20
(d) 21
Ans: We can form 19 pairs of co primes from the 2, 3, 4, 5, 6, 7, 8, 9 which are given below,
(2, 3), (2, 5), (2, 7), (2, 9), (3, 4),(3, 5), (3, 7), (3, 8), (4, 5), (4, 7), (4, 9), (5, 6), (5, 7), (5, 8), (5, 9), (6, 7), (7, 8), (7, 9) and (8, 9)
Hence, the correct answer is option (a).
Q.3. If the number 2345 a 60b is exactly divisible by 3 and 5, then the maximum value of a + b is
(a) 12
(b) 13
(c) 14
(d) 15
Ans: A number is divisible by 5 if its last digit is either 0 or 5 out of which 5 is maximum.
∴ b = 5
A number is divisible by 3 if the sum of its digits is divisible by 3
2 + 3 + 4 + 5 + 6 + 0 + 5 = 25
So, we can add maximum 8 to 25 which will give us 33 which is divisible by 3.
∴ a = 8
Now, a + b = 8 + 5 = 13
Hence, the correct answer is option (b).
Q.4. The HCF of 100 and 101 is .
(a) 1
(b) 7
(c) 37
(d) None of these
Ans: 100 = 1 × 2 × 2 × 5 × 5
101 = 1 × 101
Since, 100 is a composite number and 101 is a prime number.
Thus, their HCF is 1.
Hence, the correct answer is option (a).
Q.5. The LCM of 100 and 101 is
(a) 10100
(b) 1001
(c) 10101
(d) None of these
Ans: 100 = 1 × 2 × 2 × 5 × 5
101 = 1 × 101
Since, 100 is a composite number and 101 is a prime number.
Thus, their LCM = 100 × 101 = 10100
Hence, the correct answer is option (a).
Q.6. The greatest four digit number which when divided by 18 and 12 leaves a remainder of 4 in each case is
(a) 9976
(b) 9940
(c) 9904
(d) 9868
Ans:
18 = 1 × 2 × 3 × 3 = 21 × 32
12 = 1 × 2 × 2 × 3 = 22 × 31
LCM of 18 and 12 = 22 × 32 = 36
Largest 4-digit number is 9999
Now, if we divide 9999 by 36, we will get 277.75 as quotient.
The integer just less than 277.75 is 277
∴ Required number = (36 × 277) + 4 = 9972 + 4 = 9976
Hence, the correct answer is option (a).
Q.7. The GCD of two numbers is 17 and their LCM is 765. How many pairs of values can the numbers assume?
(a) 1 (b) 2 (c) 3 (d) 4
Ans: GCD of two numbers is 17
So, the numbers can be 17a and 17b.
Now, 17a × 17b = 17 × 765
⇒ ab = 45
So, we can get two pairs
a = 5 and b = 9 or a = 9 and b = 5
Thus, the numbers are 17 × 5 = 85 and 17 × 9 = 153.
Also, we can get the other pair 17 × 1 = 17 and 765.
Hence, the correct answer is option (b).
Q.8. The number of factors of 1080 is
(a) 32
(b) 28
(c) 24
(d) 36
Ans: 1080 = 2 × 2 × 2 × 3 × 3 × 3 × 5 = 23 × 33 × 51
Thus, the total number of factors ig given by
(3 + 1)(3 + 1)(1 + 1) = 32
Hence, the correct answer is option (a).
Q.9. The HCF of first 100 natural numbers is
(a) 2
(b) 100
(c) 1
(d) None of these
Ans: The HCF of first 100 natural numbers is 1 because there are some prime numbers like 2, 3, 5 and so on which can't have common factor other than 1.
Hence, the correct answer is option (c).
Q.10. The least number exactly divisible by 36 and 24 is
(a) 144
(b) 72
(c) 64
(d) 324
Ans: 36 = 2 × 2 × 3 × 3 = 22 × 32
24 = 2 × 2 × 2 × 3 = 23 × 31
LCM of 36 and 24 = 23 × 32 = 72
Hence, the correct answer is option (b).
Q.11. Find the HCF of all natural numbers from 200 to 478.
Ans: The HCF of all natural numbers from 200 to 478 is 1 because there are some prime numbers like 211, 233 and so on which can't have common factor other than 1.
Q.12. If x is prime, y is a composite number such that x + y = 240 and their LCM is 4199. Find x and y.
Ans: We know that the LCM of a prime number and a composite number is equal to their product.
So, xy = 4199
Now, x + y = 240
⇒ y = 240 − x
Substituting the value of y in xy = 4199, we will get
x( 240 − x) = 4199
⇒ 240x − x2 = 4199
⇒ x2 − 240x + 4199 = 0
⇒ x2 − 19x − 221x + 4199 = 0
⇒x(x − 19) − 221(x − 19) = 0
⇒ (x − 19)(x − 221) = 0
⇒ (x − 19) = 0 or (x − 221) = 0
⇒ x = 19, 221
∴ x = 19 and y = 221 or x = 221 and y = 19
Q.13. The LCM of two numbers is 1024 and one of them is a prime number. Find their HCF.
Ans: LCM of two numbers is 1024 = 210
Since, the other is prime number.
Hence, the other must be 2.
HCF of 2 and 1024 is 2.
Q.14. The HCF of two numbers is 4 and their LCM is 400. How many pairs of values can the numbers assume?
Ans: HCF of two numbers is 4
So, the numbers can be 4a and 4b.
Now, 4a × 4b = 4 × 400
⇒ ab = 100
So, we can get the pairs
a = 25 and b = 4
a = 4 and b = 25
Thus, the numbers are 4 × 25 = 100 and 4 × 4 = 16.
Also, we can get the other pair 4 × 1 = 4 and 400.
Hence, there are two pairs.
Q.15. Find the greatest number that can divide 101 and 115 leaving remainders 5 and 7 respectively.
Ans: First we will subtract 5 and 7 from 101 and 115 recpectively.
Now, we have 101 − 5 = 96 and 115 − 7 = 108
96 = 2 × 2 × 2 × 2 × 2 × 3 = 25 × 31
108 =2 × 2 × 3 × 3 × 3 = 22 × 33
HCF of 96 and 108= 22 × 31 = 12
Hence, the greatest number that can divide 101 and 115 leaving remainders 5 and 7 respectively is 12.
Q.16. Find the least three digit number which when divided by 20, 30, 40 and 50 leaves remainder 10 in each case.
Ans: 20 = 1 × 2 × 2 × 5 = 22 × 51
30 = 1 × 2 × 3 × 5 = 21 × 31 × 51
40 = 1 × 2 × 2 × 2 × 5 = 23 × 51
50 = 1 × 2 × 5 × 5 = 21 × 52
LCM of 20, 30, 40 and 50 = 23 × 31 × 52 = 600
∴ Required number = 600 + 10 = 610.
Hence, the least three digit number which when divided by 20, 30, 40 and 50 leaves remainder 10 in each case is 610.
Q.17. Find the largest number that divides 59 and 54 leaving remainders 3 and 5 respectively
Ans: First we will subtract 3 and 5 from 59 and 54 recpectively.
Now, we have 59 − 3 = 56 and 54 − 5 = 49
56 = 2 × 2 × 2 × 7 = 23 × 71
49 = 7 × 7 = 72
HCF of 56 and 49 = 71 = 7
Hence, the largest number that divides 59 and 54 leaving remainders 3 and 5 respectively is 7.
Q.18. Can two numbers have 12 as their HCF and 512 as their LCM? Justify your answer
Ans: HCF of two numbers is a factor of the LCM of those numbers
Thu, we cannot have two numbers whose HCF is 12 and LCM is 512.
Because, when we divide 512 by 12, we get a remainder of 42.68
Thus, 12 is not a factor of 512.
Hence, we cannot have two numbers of whose HCF is 12 and LCM is 512.
Q.19. Write all prime numbers between 50 and 100.
Ans: The prime numbers between 50 and 100 are given below:
53, 59, 61, 67, 71, 73, 79, 83, 89 and 97.
Q.20. Find the least 5-digit number which is exactly divisible by 20, 25 and 30.
Ans: 20 = 1 × 2 × 2 × 5 = 22 × 51
25 = 1 × 5 × 5 × 31 = 52
30 = 1 × 2 × 3 × 5 = 21 × 31 × 51
LCM of 20, 25 and 30 = 22 × 31 × 52 = 300
Least five digit number is 10000
Now, if we divide 10000 by 60, we will get 33.33 as quotient.
The integer just greater than 33.33 is 34
∴ Required number = 300 × 34 = 10200
Hence, the least 5-digit number which is exactly divisible by 20, 25, 30 is 10200.
Q.21. The least number which when divided by 6, 9, 12 and 18 leaves no remainder is
Ans: 6 = 2 × 3 = 21 × 31
9 = 3 × 3 = 32
12 = 2 × 2 × 3 = 22 × 31
18 = 2 × 3 × 3 = 21 × 32
LCM of 6, 9, 12 and 18 = 22 × 32 = 36
Hence, the least number which when divided by 6, 9, 12 and 18 leaves no remainder is 36
Q.22. If the product of two numbers is 360 and their HCF is 6, then their LCM is
Ans: Product of two numbers = HCF of two numbers × LCM of two numbers
⇒ 360 = 6 × LCM of two numbers
⇒ LCM of two numbers = 360/6=60
Q.23. The least number which when divided by 5, 7 and 8 leaves 3 as remainder in each case is
Ans: LCM of 5, 7 and 8 is 5 × 7 × 8 = 280.
The least number which when divided by 5, 7 and 8 leaves 3 as remainder in each case is given by
280 + 3
= 283
Q.24. The LCM of two numbers is 26. The possible values of HCF are .......
Ans: 26 = 1 × 2 × 13
So, the possible values of HCF are 1, 2 and 13.
Q.25. Two perfect numbers are ......... and ...........
Ans: A perfect number is a positive number that equals the sum of its divisors, excluding itself.
Divisors of 6 = 1, 2, 3
Divisors of 28 = 1, 2, 4, 7, 14, 28
In 6, the sum of divisors except itself, 1 + 2 + 3 is 6.
In 28, the sum of divisors except itself, 1 + 2 + 4 + 7 + 14 is 28.
Therefore, two perfect numbers are 6 and 28.
|
92 videos|348 docs|54 tests
|

|
Explore Courses for Class 6 exam
|

|

















