RS Aggarwal Solutions: Factors & Multiples (Exercise 2C) | Mathematics for Class 6 PDF Download
Find the prime factorization of each of the following numbers.
Q.1. 12.
Ans. We have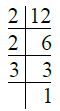
∴ 12 = 2 × 2 × 3 = 22 × 3.
Q.2. 18.
Ans. We have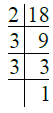
∴ 18 = 2 × 3 × 3
= 2 × 32.
Q.3. 48.
Ans. We have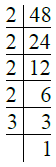
∴ 48 = 2 × 2 × 2 × 2 × 3
= 24 × 3.
Q.4. 56.
Ans. We have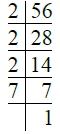
∴ 56 = 2 × 2 × 2 × 7
= 23 × 7.
Q.5. 90.
Ans. We have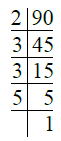
∴ 90 = 2 × 3 × 3 × 5
= 2 × 32 × 5.
Q.6. 136.
Ans. We have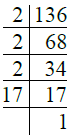
∴ 136 = 2 × 2 × 2 × 17
= 23 × 17.
Q.7. 252.
Ans. We have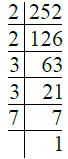
∴ 252 = 2 × 2 × 3 × 3 × 7
= 22 × 32 × 7.
Q.8. 420.
Ans. We have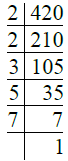
∴ 420 = 2 × 2 × 3 × 5 × 7
= 22 × 3 × 5 × 7.
Q.9. 637.
Ans. We have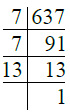
∴ 637 = 7 × 7 × 13
= 72 × 13.
Q.10. 945.
Ans. We have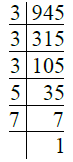
∴ 945 = 3 × 3 × 3 × 5 × 7
= 33 × 5 × 7.
Q.11. 1224.
Ans. We have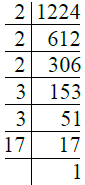
∴ 1224 = 2 × 2 × 2 × 3 × 3 × 17
= 23 × 32 × 17.
Q.12. 1323.
Ans. We have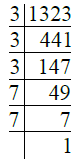
∴ 1323 = 3 × 3 × 3 × 7 × 7
= 33 × 72.
Q.13. 8712.
Ans. We have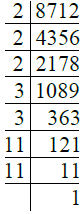
∴ 8712 = 2 × 2 × 2 × 3 × 3 × 11 × 11
= 23 × 32 × 112.
Q.14. 9317.
Ans. We have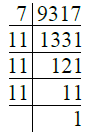
∴ 9317 = 7 × 11 × 11 × 11
= 7 × 113.
Q.15. 1035.
Ans. We have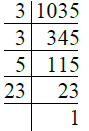
∴ 1035 = 3 × 3 × 5 × 23
= 32 × 5 × 23.
Q.16. 1197.
Ans. We have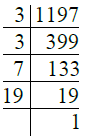
∴ 1197 = 3 × 3 × 7 × 19
= 32 × 7 × 19.
Q.17. 4641.
Ans. We have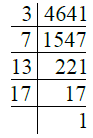
∴ 4641 = 3 × 7 × 13 × 17.
Q.18. 4335.
Ans. We have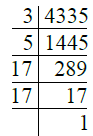
∴ 4335 = 3 × 5 × 17 × 17 = 3 × 5 × 172.
Q.19. 2907.
Ans. We have
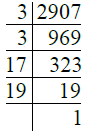
∴ 2907 = 3 × 3 × 17 × 19 = 32 × 17 × 19.
Q.20. 13915.
Ans. We have
∴ 13915 = 5 × 11 × 11 × 23 = 5 × 112 × 23
H.C.F. AND L.C.M.
Highest Common Factor (H.C.F.).
The greatest number which is a common factor of two or more given numbers, is called highest common factor (H.C.F.) or greatest common divisor (G.C.D.) or greatest common measure (G.C.M.).
To find H.C.F. (By Prime Factorization Method).
We first find the prime factorization of each of the given numbers. Then, the product of all common prime factors, using the least power of each common prime factor, is the H.C.F. of the given numbers.
To find H.C.F. (By Division Method).
To find the H.C.F. of two given numbers, we divide the greatest number by smaller one. Next, divide the divisor by the remainder. Go on repeating the process of dividing the preceding divisor by the remainder last obtained, till the remainder is zero. Then, last divisor is the required H.C.F. of the given numbers.
To find the H.C.F. of more than two numbers, first we find the H.C.F. of two numbers. The H.C.F. of this H.C.F. and the third number gives the H.C.F. of these three numbers and so on.
Lowest Common Multiple (L.C.M.).
The lowest common multiple of two or more numbers is the smallest number which is a multiple of each of the numbers.
To find L.C.M. (By Prime Factorization Method).
To find the L.C.M. of two or more numbers, we write the prime factorization of each of the given numbers. Then the product of all different prime factors of the given numbers, using the greatest power of each common prime factor, is the required L.C.M. of these numbers.
To find L.C.M. (By Division Method).
In this method, we arrange the given numbers in a line, in any order. We divide by a number which divides exactly at least two of the given numbers and carry forward the numbers which are not divisible. This process is repeated till no two of the given numbers are divisible by a same number. The product of the divisors and the undivided numbers is the required L.C.M. of the given numbers.
Properties of H.C.F. and L.C.M. of Given Numbers
1. The H.C.F. of given numbers is not greater than any of the given numbers.
2. The H.C.F. of two co-primes is 1.
3. The L.C.M. of given numbers is not less than any of the given numbers.
4. The L.C.M. of two co-primes is equal to their product.
5. The H.C.F. of given numbers is always a factor of their L.C.M.
6. If a and b are two given numbers such that a is a factor of b their H.C.F. = a
and their L.C.M. = b.
7. If two numbers are given then product of two numbers = product of their
H.C.F. and L.C.M.
Remark. For any two given numbers, we have :
(i) L.C.M.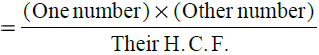
(ii) H.C.F.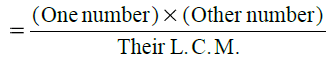
|
48 videos|334 docs|23 tests
|
FAQs on RS Aggarwal Solutions: Factors & Multiples (Exercise 2C) - Mathematics for Class 6
| 1. What are factors and multiples? |  |
| 2. How do you find the factors of a number? |  |
| 3. How do you find the multiples of a number? |  |
| 4. What is the difference between factors and multiples? |  |
| 5. Can a number be both a factor and a multiple? |  |
















