RS Aggarwal Solutions: Factors & Multiples (Exercise 2D) | Mathematics (Maths) Class 6 PDF Download

First we find the H.C.F. of 161 and 207Find the H.C.F. of the numbers in each of the following, using the prime factorization method :

Q.1. 84, 98.
Ans. We have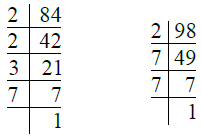

So, 84 = 2 × 2 × 3 × 7 = 22 × 3 × 7
98 = 2 × 7 × 7 = 2 × 72
∴ H.C.F. = 2 × 7 = 14.

Q.2. 170, 238.
Ans.
We have

So, 170 = 2 × 5 × 17
238 = 2 × 7 × 17

∴ H.C.F. of 170 and 238 = 2 × 17 = 34.

Q.3. 504, 980.
Ans. We have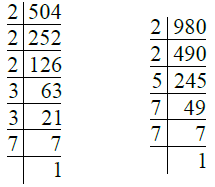

So, 504 = 2 × 2 × 2 × 3 × 3 × 7 = 2³ × 3² × 7
980 = 2 × 2 × 5 × 7 × 7 = 2² × 5 × 7²
∴ H.C.F. of 504 and 980 = 2. × 7
= 4 × 7 = 28.

Q.4. 72, 108, 180.
Ans. We have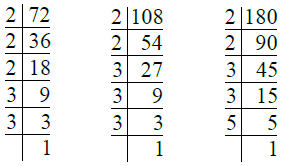

So, 72 = 2 × 2 × 2 × 3 × 3 = 2³ × 3²
108 = 2 × 2 × 3 × 3 × 3 = 2² × 3³
180 = 2 × 2 × 3 × 3 × 5 = 2² × 3² × 5
∴ H.C.F. of 72, 108,
180 = 22 × 32
= 4 × 9 = 36

Q.5. 84, 120, 138.
Ans. We have
So, 84 = 2 × 2 × 3 × 7
= 2² × 3 × 7

120 = 2 × 2 × 2 × 3 × 5
= 2³ × 3 × 5
138 = 2 × 3 × 23
∴ H.C.F. of 84, 120 and
138 = 2 × 3 = 6.

Q.6. 106, 159, 371.
Ans. We have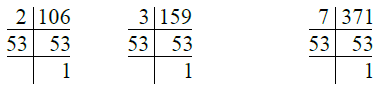

So, 106 = 2 × 53
159 = 3 × 53
371 = 7 × 53
∴ H.C.F. of 106, 159, 371 = 53.

Q.7. 272, 425.

Ans. We have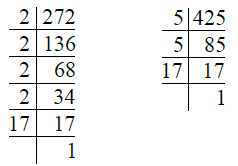

So, 272 = 2 × 2 × 2 × 2 × 17 = 2⁴ × 17
425 = 5 × 5 × 17
= 5² × 17
∴ H.C.F. of 272 and 425 = 17.

Q.8. 144, 252, 630.
Ans. We have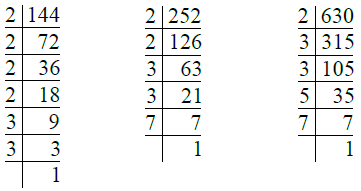

So, 144 = 2 × 2 × 2 × 2 × 3 × 3 = 2⁴ × 3²
252 = 2 × 2 × 3 × 3 × 7 = 2² × 3² × 7

630 = 2 × 3 × 3 × 5 × 7 = 2 × 3² × 5 × 7
∴ H.C.F. of 144, 252 and 630 = 2 × 3²
= 2 × 9 = 18.

Q.9. 1197, 5320, 4389.
Ans. We have

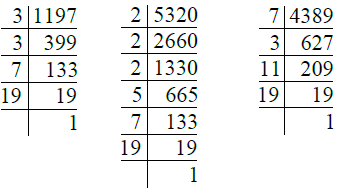
So, 1197 = 3 × 3 × 7 × 19 = 3² × 7 × 19
5320 = 2 × 2 × 2 × 5 × 7 × 19
= 2³ × 5 × 7 × 19
4389 = 7 × 3 × 11 × 19

∴ H.C.F. of 1197, 5320,
4389 = 7 × 19 = 133.

Find the H.C.F. of the numbers in each of the following using division method :

Q.10. 58, 70.

Ans. By division method, we have :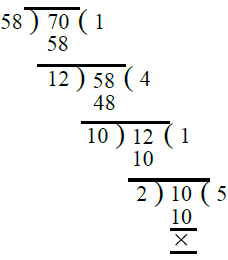

∴ H.C.F. of 58 and 70 = 2.

Q.11. 399, 437.
Ans. By division method, we have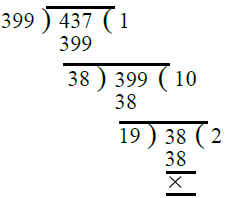

∴ H.C.F. of 399 and 437 = 19.

Q.12. 1045, 1520.
Sol. By division method, we have

∴ H.C.F. of 1045 and 1520 = 95.

Q.13. 1965, 2096.
Ans. By division method, we have

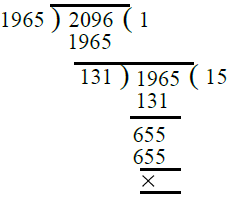
∴ H.C.F. of 1965 and 2096 = 131.

Q.14. 2241, 2324.
Ans. By division method, we have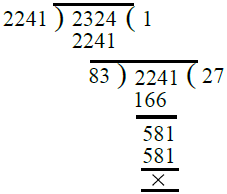

∴ H.C.F. of 2241 and 2324 = 83.

Q.15. 658, 940, 1128.
Ans. First, we find the H.C.F. of 658 and 940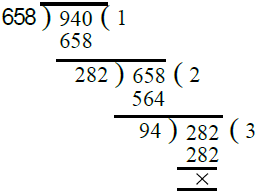

∴ H.C.F. of 658 and 940 is 94.
Now, we find the H.C.F. of 94 and 1128.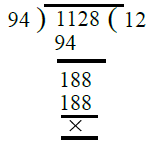

∴ H.C.F. of 94 and 1128 = 94
Hence, H.C.F. of 658, 940 and 1128
= 94.

Q.16. 754, 1508, 1972.
Ans. First, we find the H.C.F. of 754 and 1508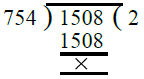

∴ H.C.F. of 754 and 1508 is 754
Now, we find the H.C.F. of 754 and 1972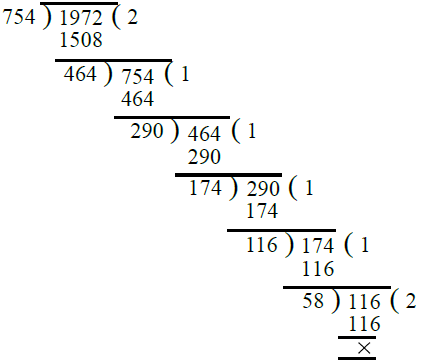

∴ H.C.F. of 754 and 1972 = 58
Hence, the H.C.F. of 754, 1508 and 1972
= 58.

Q.17. 391, 425, 527.
Ans. First, we find the H.C.F. of 391 and 425.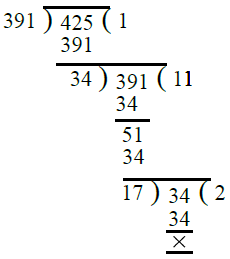

∴ H.C.F. of 391 and 425 is 17.
Now, we find the H.C.F. of 17 and 527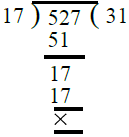

∴ H.C.F. of 17 and 527 is 17
Hence, H.C.F. of 391, 425 and 527 = 17.

Q.18. 1794, 2346, 4761.
Ans. First, we find the H.C.F. of 1794 and 2346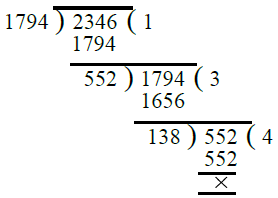

∴ H.C.F. of 1794 and 2346 is 138.
Now, we find the H.C.F. of 138 and 4761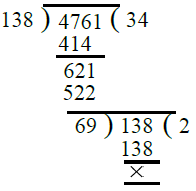

∴ H.C.F. of 138 and 4761 is 69.
Hence, the H.C.F. of 1794, 2346 and 4761 = 69.
Show that the following pairs are coprimes:

Q.19. 59, 97.
Ans. First, we find the H.C.F. of 59, 97.

∴ H.C.F. of 59 and 97 is 1.
Hence 59 and 97 are co-prime.

Q.20. 161, 192.
Ans. First, we find the H.C.F. of 161 and 192.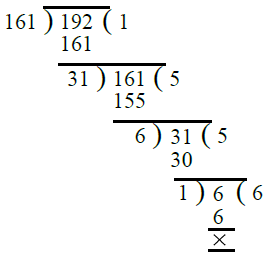

∴ H.C.F. of 161 and 192 is 1.
Hence 161 and 192 are co-prime.

Q.21. 343, 432.
Ans. First, we find the H.C.F. of 343 and 432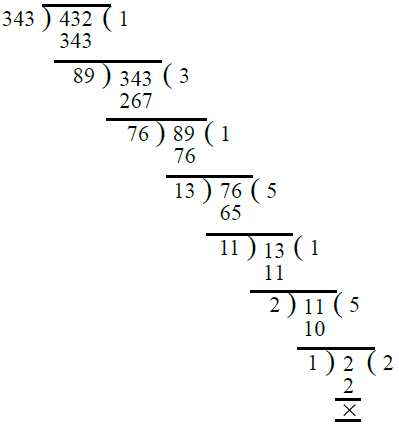

∴ H.C.F. of 343 and 432 is 1.
Hence 343 and 432 are co-prime.

Q.22. 512, 945.
Ans. First, we find the H.C.F. of 512 and 945.

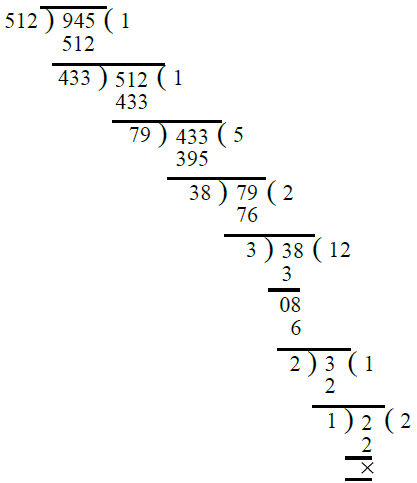
∴ H.C.F. of 512 and 945 is 1.
Hence 512 and 945 are co-prime.

Q.23. 385, 621.
Ans. First, we find the H.C.F. of 385 and 621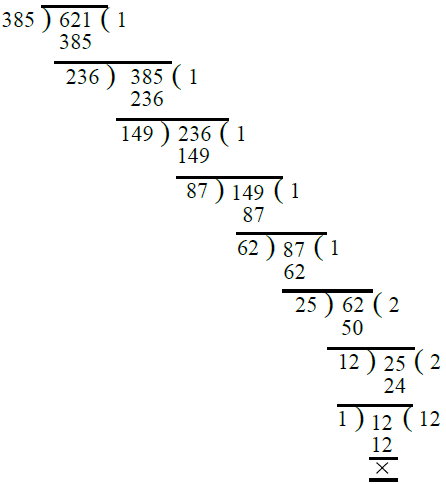

∴ H.C.F. of 385 and 621 is 1.
Hence the numbers 385 and 621 are co-prime.

Q.24. 847, 1014.
Ans. First, we find the H.C.F. of 847 and 1014.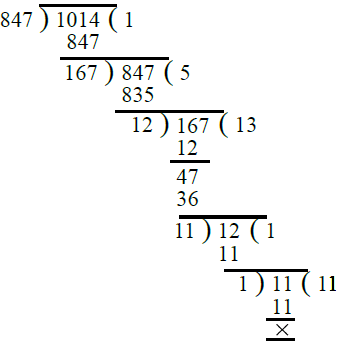

∴ H.C.F. of 847 and 1014 is 1.
Hence 847 and 1014 are co-prime.

Q.25. Find the greatest number which divides 615 and 963 leaving the remainder 6 in each case.
Ans. Clearly, we have to find the greatest number which divides (615 – 6) and (963 – 6) exactly.
So, the required number = H.C.F. of 615 – 6 = 609 and 963 – 6 = 957

∴ The required greatest number = 87.

Q.26. Find the greatest number which divides 2011 and 2623 leaving remainders 9 and 5 respectively.
Ans. Clearly, we have to find the greatest number which divides 2011 – 9 = 2002 and 2623 – 5 = 2618.
So, the required greatest number = H.C.F. of 2002 and 2618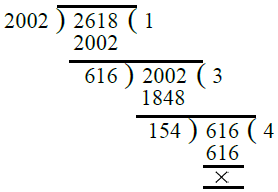

∴  Required greatest number = 154.

Q.27. Find the greatest number that will divide 445, 572 and 699 leaving remainders 4,5, 6 respectively.

Ans. Clearly, we have to find the greatest number which divides (445 – 4), (572 – 5) and (699 – 6). So, the required number = H.C.F. of 441, 567 and 693. First we find the H.C.F. of 441 and 567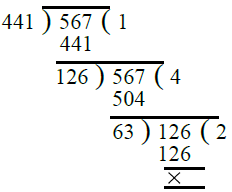

∴ H.C.F. of 441 and 567 is 63
Also,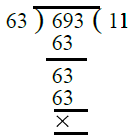

So H.C.F. of 63 and 693 is 63
Hence the required number = 63.

Q.28. Reduce each of the following fractions to the lowest terms :
(i)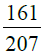
(ii)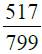
(iii)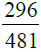
Ans.
(i) The given fraction =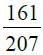  
First we find the H.C.F. of 161 and 207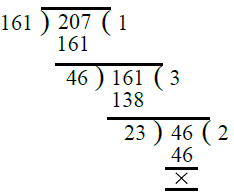

∴ H.C.F. of 161 and 207 = 23
Dividing the numerator and the denominator of the given function by 23, we get :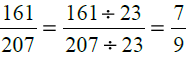

(ii) The given fraction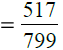
First we find the H.C.F. of 517 and 799 as under :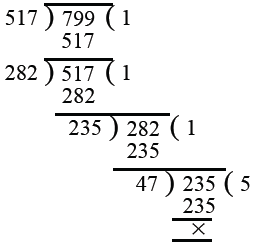

∴ H.C.F. of 517 and 799 is 47.
Dividing the numerator and the denominator of the given fraction by 47, we get :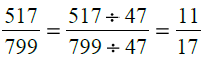

(iii) The given fraction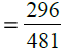
First we find the H.C.F. of 296 and 481 as under :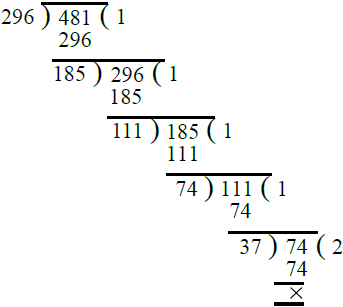

∴ H.C.F. of 296 and 481 is 37.

Dividing the numerator and denominator of the given fraction by 37, we get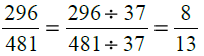


Q.29. Three pieces of timber 42 metres, 49 metres and 63 metres long have to be divided into planks of the same length. What is the greatest possible length of each plank ?
Ans.

Lengths of three pieces of timber = 42 metres, 49 metres, 63 metres
Greatest possible length of each plank = H.C.F. of 42 metres, 49 metres and

63 metres
First we find the H.C.F. of 42 and 49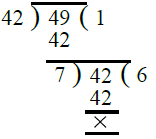

∴ H.C.F. of 42 and 49 = 7
Now we find the H.C.F. of 7 and 63

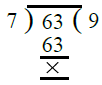
So, the H.C.F. of 7 and 63 is 7
∴ H.C.F. of 42 metres, 49 metres of 63 metres = 7 metres
Hence required possible length of each
plank = 7 metres.

Q. 30. Three different containers contain 403 L, 434 L and 465 L of milk respectively. Find the capacity of a container which can measure the milk of all the containers an exact number of times.
Ans. Quantity of milk in three different containers = 403 L, 434 L and 465 L
Clearly, the maximum capacity of the required container = H.C.F. of 403 L,
434 L, 465 L, we have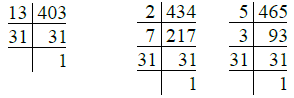

∴ 403 = 13 × 31
434 = 2 × 7 × 31
465 = 5 × 3 × 31
So the H.C.F. of 403 L, 434 L and 465 L = 31 L
Maximum capacity of the required container = 31 L.

Q.31. There are 527 apples, 646 pears and 748 oranges. These are to be arranged in heaps containing the same number of fruits. Find the greatest number of fruits possible in each heap. How many heaps are formed ?
Ans.
The given fruits = 527 apples, 646 pears and 748 oranges
Clearly, the greatest number of fruits in each heap = H.C.F. of 527, 646 and 748
we have

∴ 527 = 17 × 31
646 = 2 × 17 × 19
748 = 2 × 2 × 11 × 17
So, the H.C.F. of 527, 646 and 748 = 17
∴ Required number of fruits in each heap
= 17
Total number of fruits = 527 + 646 + 748
= 1921
Number of heaps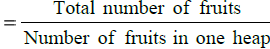

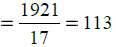
Q.32. Determine the longest tape which can be used to measure exactly the lengths 7 metres, 3 metres 85 cm and 12 metres 95 cm.
Ans.
The given lengths are :

7 metres = 7 × 100 cm = 700 cm
3 metres 85 cm = (3 × 100 + 85) cm
= 385 cm

12 metres 95 cm = (12 × 100 + 95) cm
= 1295 cm
Clearly, the length of the required longest tape

= H.C.F. of 700 cm, 385 cm and 1295 cm
We have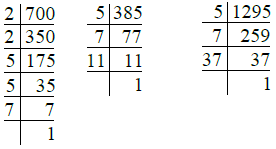

So, 700 = 2 × 2 × 5 × 5 × 7
= 2² × 5² × 7
385 = 5 × 7 × 11

1295 = 5 × 7 × 37
∴ H.C.F. of 700, 385 and
1295 = 5 × 7 = 35

The required length of the longest tape

= 35 cm.

Q.33. A rectangular courtyard is 18 m 72 cm long and 13 m 20 cm broad. It is to be paved with square tiles of the same size. Find the least possible number of such tiles.
Ans.
Length of the courtyard = 18 m 72 cm
= (18 × 100 + 72) cm
= 1872 cm
Breadth of the courtyard = 13 m 20 cm
= (13 × 100 + 20) cm

= 1320 cm
Greatest side of each of the square tiles
= H.C.F. of 1872 cm and 1320 cm
Now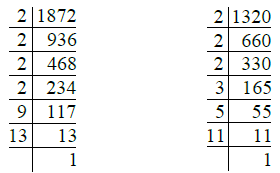

∴ 1872 = 2 × 2 × 2 × 2 × 9 × 13
= 2⁴ × 3² × 13
1320 = 2 × 2 × 2 × 3 × 5 × 11

= 2³ × 3 × 5 × 11
So, the H.C.F. of 1872 and 1320
= 2³ × 3 = 8 × 3 = 24
∴ Greatest side of the square tile
= 24 cm
Now Area of the courtyard
= Length × Breadth
= 1872 × 1320 cm²
Area of one square tile = Side × Side

= 24 × 24 cm²
∴ Least possible number of such tiles

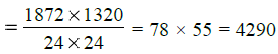
Q.34. Find the H.C.F. of :
(i) two prime numbers
(ii) two consecutive numbers
(iii) two co-primes
(iv) 2 and an even number.
Ans. (i) Let the two prime numbers be 13 and 17, we find the H.C.F. of 13 and 17 as under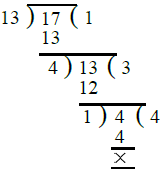

∴ H.C.F. of two prime numbers 13 and 17 = 1.
(ii) Let the two consecutive numbers be 59 and 60. We find the H.C.F. of 59 and 60 as
under :

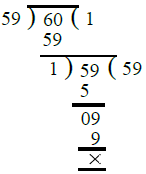
∴ H.C.F. of two consecutive numbers 59 and 60 = 1.
(iii) Let the two co-primes be 45 and 56. We find the H.C.F. of 45 and 56 as under :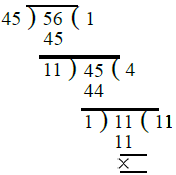

∴ H.C.F. of two co-primes 45 and 56 = 1.
(iv) We take 2 and another even number = 48 and find the H.C.F. of 2 and 48 as under :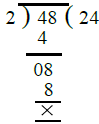

∴ H.C.F. of 2 and an even number 48 = 2.