RS Aggarwal Solutions: Factors & Multiples (Exercise 2E) | Mathematics (Maths) Class 6 PDF Download
Find the L.C.M. of the numbers given below :
Q.1. 42, 63
Ans. We have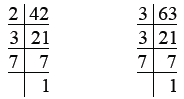
So, 42 = 2 × 3 × 7
63 = 3 × 3 × 7
= 32 × 7
∴ L.C.M. of 42 and 63 = 2 × 32 × 7
= 2 × 9 × 7
= 18 × 7 = 126
Q.2. 60, 75
Ans. We have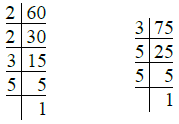
So, 60 = 2 × 2 × 3 × 5 = 22 × 3 × 5
75 = 3 × 5 × 5 = 3 × 52
L.C.M. of 60 and 75 = 22 × 3 × 52
= 4 × 3 × 25
= 4 × 75 = 300
Q.3. 12. 18, 20
Ans. We have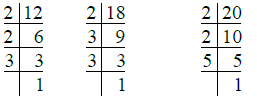
So, 12 = 2 × 2 × 3 = 22 × 3
18 = 2 × 3 × 3 = 2 × 32
20 = 2 × 2 × 5 = 22 × 5
∴ L.C.M. of 12, 18 and 20 = 22 × 32 × 5
= 4 × 9 × 5
= 20 × 9 = 180
Q.4. 36, 60, 72
Ans. We have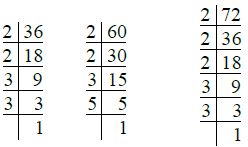
∴ 36 = 2 × 2 × 3 × 3 = 22 × 32
60 = 2 × 2 × 3 × 5 = 22 × 3 × 5
72 = 2 × 2 × 2 × 3 × 3 = 23 × 32
∴ L.C.M. of 36, 60 and 72 = 23 × 32 × 5
= 8 × 9 × 5
= 40 × 9 = 360
Q.5. 36, 40, 126
Ans. We have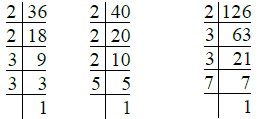
So, 36 = 2 × 2 × 3 × 3 = 22 × 32
40 = 2 × 2 × 2 × 5 = 23 × 5
126 = 2 × 3 × 3 × 7 = 2 × 32 × 7
L.C.M. of 36, 40 and 126
= 23 × 32 × 5 × 7
= 8 × 9 × 5 × 7
= 72 × 35 = 2520
Q.6. 16, 28, 40, 77
Ans.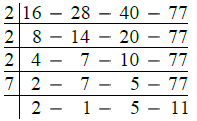
∴ L.C.M. of given numbers
= 2 × 2 × 2 × 7 × 2 × 5 × 11
= 8 × 14 × 55
= 112 × 55 = 6160
Q.7. 28, 36, 45, 60
Ans.
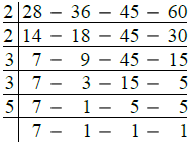
∴ L.C.M. of given numbers
= 2 × 2 × 3 × 3 × 5 × 7
= 36 × 35 = 1260
Q.8. 144, 180, 384
Ans.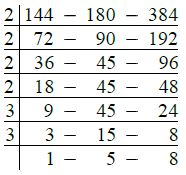
∴ L.C.M. of given numbers
= 2 × 2 × 2 × 2 × 3 × 3 × 5 × 8
= 16 × 9 × 40 = 144 × 40 = 5760
Q.9. 48, 64, 72, 96, 108
Ans.
∴ L.C.M. of given numbers
= 2 × 2 × 2 × 2 × 2 × 3 × 3 × 2 × 3
= 32 × 54 = 1728
Find the H.C.F. and L.C.M. of :
Q.10. 117, 221
Ans. First we find the H.C.F. of the given numbers as under :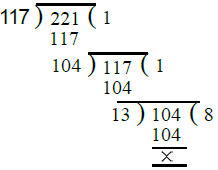
∴ H.C.F. of 117 and 221 = 13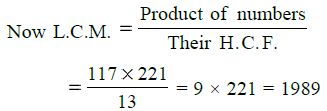
∴ H.C.F. = 13 and L.C.M. = 1989
Q.11. 234, 572
Ans. First we find the H.C.F. of 234 and 572 as under :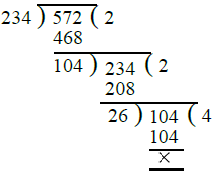
∴ H.C.F. of 234 and 572 = 26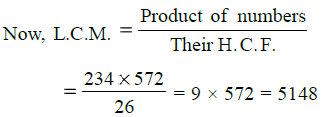
Q.12. 693, 1078
Ans. First we find the H.C.F. of 693 and 1078 as under :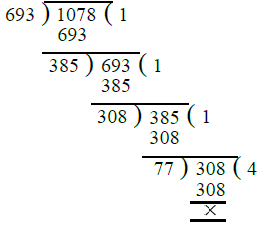
∴ H.C.F. of 693 and 1078 = 77
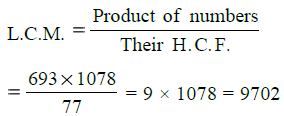
∴ H.C.F. = 77 and L.C.M. = 9702
Q.13. 145, 232
Ans. First we find the H.C.F. of 145 and 232 as under :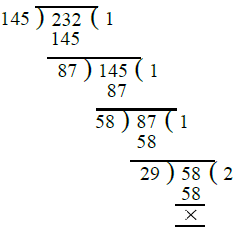
∴ H.C.F. of 145 and 232 = 29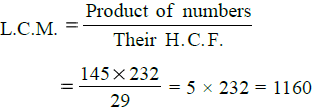
∴ H.C.F. = 29 and L.C.M. = 1160
Q.14. 861, 1353
Ans. First we find the H.C.F. of 861 and 1353 as under :
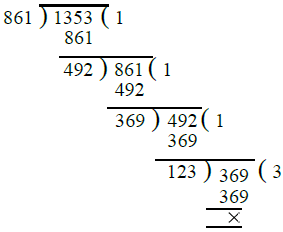
∴ H.C.F. of 861 and 1353 = 123
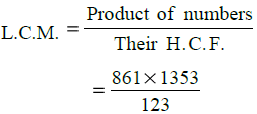
= 7 × 1353 = 9471
∴ H.C.F. = 123 and L.C.M. = 9471
Q.15. 2923, 3239
Ans. First we find the H.C.F. of 2923 and 3239 as under :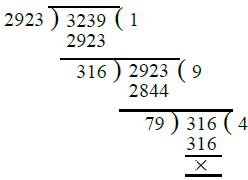
∴ H.C.F. of 2923 and 3239 = 79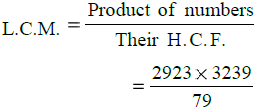
= 37 × 3239 = 119843
∴ H.C.F. = 79 and L.C.M. = 119843
Q.16. For each pair of numbers, verify that their product = (H.C.F. × L.C.M.)
(i) 87, 145
(ii) 186, 403
(iii) 490, 1155
Ans.
(i) We have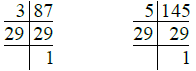
So, 87 = 3 × 29
145 = 5 × 29
∴ H.C.F. of 87 and 145 = 29
L.C.M. of 87 and 145 = 3 × 5 × 29
= 15 × 29 = 435
Now product of 87 and 145 = 87 × 145
= 12615
Their H.C.F. × L.C.M. = 29 × 435
= 12615
Hence verified.
(ii) We have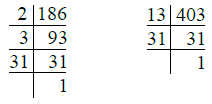
So, 186 = 2 × 3 × 31
403 = 13 × 31
∴ H.C.F. of 186 and 403 = 31
L.C.M. of 186 and 403
= 2 × 3 × 13 × 31 = 2418
Now product of 186 and 403
= 186 × 403 = 74958
Their H.C.F. × L.C.M. = 31 × 2418
= 74958
Hence verified.
(iii) 490, 1155
We have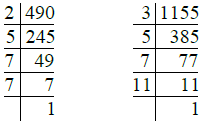
So, 490 = 2 × 5 × 7 ×7 = 2 × 5 × 72
1155 = 3 × 5 × 7 × 11
H.C.F. of 490 and 1155 = 5 × 7 = 35
L.C.M. of 490 and 1155
= 2 × 3 × 5 × 72 × 11
= 2 × 3 × 5 × 49 × 11
= 30 × 539 = 16170
Now, product of 490 and 1155
= 490 × 1155 = 565950
Their H.C.F. × L.C.M. = 35 × 16170
= 565950
Hence verified.
Q.17. The product of two numbers is 2160 and their H.C.F. is 12. Find their L.C.M.
Ans. We know that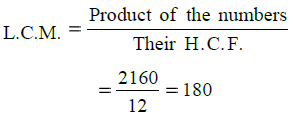
Q.18. The product of two numbers is 2560 and their L.C.M. is 320. Find their H.C.F.
Ans. We know that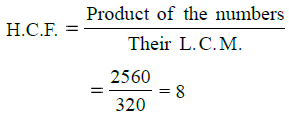
Q.19. The H.C.F. of two numbers is 145 and their L.C.M. is 2175. If one of the numbers is 725, find the other.
Ans.
We know that
One number × The other number
= H.C.F. × L.C.M.
∴ The other number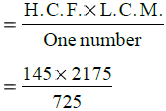
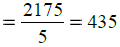
∴ Required number = 435
Q.20. The H.C.F. and L.C.M. of two numbers are 131 and 8253 respectively. If one of the numbers is 917, find the other.
Ans.
We know that
One number × The other number
= H.C.F. × L.C.M.
∴ The other number
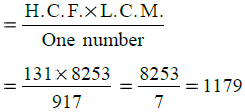
∴ Required number = 1179
Q.21. Find the least number divisible by 15, 20, 24, 32 and 36.
Ans. Required least number = L.C.M. of 15, 20, 24, 32 and 36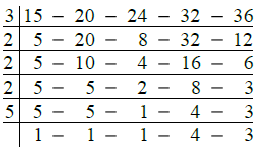
∴ L.C.M. = 3 × 2 × 2 × 2 × 5 × 4 × 3
= 24 × 60 = 1440
Hence, required least number = 1440
Q.22. Find the least number which when divided by 25, 40 and 60 leaves 9 as the remainder in each case.
Ans. Clearly, required least number = (L.C.M. of the given numbers + 9)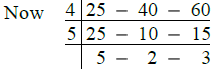
∴ L.C.M. of the given numbers
= 4 × 5 × 5 × 2 × 3
= 600
∴ Required least number = 600 + 9
= 609
Q.23. Find the least number of five digits that is exactly divisible by 16, 18, 24 and 30.
Ans.
First we find the L.C.M. of the given numbers as under :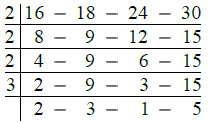
∴ L.C.M. of the given numbers
= 2 × 2 × 2 × 3 × 2 × 3 × 5
= 24 × 30 = 720
Now least number of five digits = 10000
Dividing 10000 by 720, we get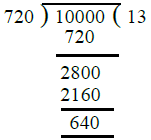
Clearly if we add 80 to 640, it will become 720 which is exactly divisible by 720.
∴ Required least number of five digits
= 10000 + 80 = 10080
Q. 24. Find the greatest number of five digits exactly divisible by 9, 12, 15, 18 and 24.
Ans. The greatest number of five digits exactly divisible by the given numbers = The greatest number of five digits exactly divisible by the L.C.M. of given numbers.
Now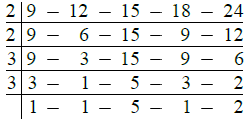
∴ L.C.M. of given numbers
= 2 × 2 × 3 × 3 × 5 × 2
= 360
Now greatest number of five digits
= 99999
Dividing 99999 by 360, we get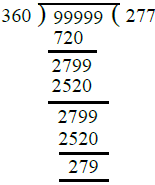
∴ Required greatest number of five digits
= 99999 – 279
= 99720
Q.25. Three bells toll at intervals of 9, 12, 15 minutes respectively. If they start tolling together, after what time will they next toll together ?
Ans.
Three bells will again toll together after an interval of time which is exactly divisible by 9, 12, 15 minutes.
∴ Required time = L.C.M. of 9, 12, 15 minutes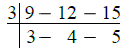
∴ L.C.M. of 9, 12, 15 minutes
= 3 × 3 × 4 × 5 minutes
= 9 × 20 minutes
= 180 minutes
∴ Required time = 180 minutes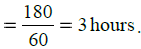
Q. 26. Three boys step off together from the same place. If their steps measure 36 cm, 48 cm and 54 cm, at what distance from the starting point will they again step together ?
Ans. Required distance = L.C.M. of 36 cm, 48 cm and 54 cm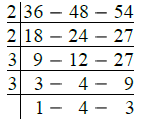
∴ L.C.M. of 36 cm, 48 cm, 54 cm
= 2 × 2 × 3 × 3 × 4 × 3 cm
= 36 × 12 cm
= 432 cm
= 4 m 32 cm
∴ Required distance = 4 m 32 cm.
Q. 27. The traffic lights at three different road crossings change after every 48 seconds, 72 seconds and 108 secondsrespectively. If they start changing simultaneously at 8 a.m., after how much time will they change again simultaneously ?
Ans. Required time = L.C.M. of 48 seconds, 72 seconds and 108 seconds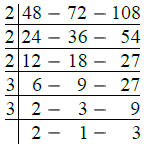
∴ L.C.M. of 48 sec., 72 sec. and 108 sec.
= 2 × 2 × 2 × 3 × 3 × 2 × 3 sec.
= 24 × 18 sec.
= 432 sec.
∴ Required time = 432 sec.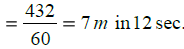
Q.28. Three measuring rods are 45 cm, 50 cm and 75 cm in length. What is the least length (in metres) of a rope that can be measured by the full length of each of these three rods ?
Ans.
Lengths of three rods = 45 cm, 50 cm and 75 cm
Required least length of the rope = L.C.M. of 45 cm, 50 cm, 75 cm
We have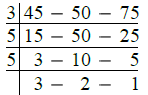
∴ L.C.M. of 45 cm, 50 cm and 75 cm
= 3 × 5 × 5 × 3 × 2 cm
= 15 × 30 cm
= 450 cm
∴ Required length of the rope = 450 cm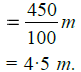
Q.29. An electronic device makes a beep after every 15 minutes. Another device makes a beep after every 20 minutes. They beeped together at 6 a.m. At what time will they next beep together ?
Ans.
The time after which both the devices will beep together = L.C.M. of 15 minutes and 20 minutes
Now,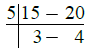
∴ L.C.M. of 15 minutes and 20 minutes
= 5 × 3 × 4
= 60 minutes
= 1 hour
∴ Both the devices will beep together after 1 hour from 6 a.m.
∴ Required time = 6 + 1
= 7 a.m.
Q.30. The circumferences of four wheels are 50 cm, 60 cm, 75 cm and 100 cm respectively. They start moving simultaneously. What least distance should they cover so that each wheel makes a complete number of revolutions ?
Ans.
The circumferences of four wheels = 50 cm, 60 cm, 75 cm and 100 cm
Required least distance = L.C.M. of 50 cm, 60 cm, 75 cm and 100 cm
Now,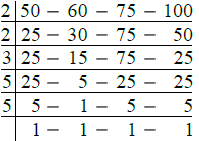
∴ L.C.M. of 50 cm, 60 cm, 75 cm, 100 cm
= 2 × 2 × 3 × 5 × 5 cm
= 300 cm = 3 m
∴ Required least distance = 3 m.
|
92 videos|348 docs|54 tests
|
FAQs on RS Aggarwal Solutions: Factors & Multiples (Exercise 2E) - Mathematics (Maths) Class 6
| 1. What is the difference between factors and multiples? |  |
| 2. How can I find the factors of a given number? |  |
| 3. What is the difference between common factors and common multiples? |  |
| 4. How can I find the common factors of two numbers? |  |
| 5. Can a number be its own factor or multiple? |  |

|
Explore Courses for Class 6 exam
|

|

















