RS Aggarwal Solutions: Whole Numbers (Exercise 3D) | Mathematics (Maths) Class 6 PDF Download

Q.1. Fill in the blanks to make each of the following a true statement :
(i) 246 × 1 = ................
(ii) 1369 × 0 = ............
(iii) 593 × 188 = 188 × .........
(iv) 286 × 753 = ............ × 286
(v) 38 × (91 × 37) = ............. × (38 × 37)
(vi) 13 × 100 × ............. = 1300000
(vii) 59 × 66 + 59 × 34 = 59 × (................+ .............)
(viii) 68 × 95 = 68 × 100 – 68 × .............

Ans. (i) 246 × 1 = 246
(By multiplicative property of 1)
(ii) 1369 × 0 = 0
(By multiplicative property of 0)
(iii) 593 × 188 = 188 × 593

(By commutative law of multiplicaton)

(iv) 286 × 753 = 753 × 286

(By commutative law of multiplication)

(v) 38 × (91 × 37) = 91 × (38 × 37)

(By associative law of multiplication)

(vi) 13 × 100 × 1000 = 1300000

(vii) 59 × 66 + 59 × 34 = 59 × (66 + 34)

(By distributive law of multiplication)

(viii) 68 × 95 = 68 × 100 – 68 × 5

Q.2. State the property used in each of the following statements :
(i) 19 × 17 = 17 × 19
(ii) 16 × 32 is a whole number
(iii) (29 × 36) × 18 = 29 × (36 × 18)
(iv) 1480 × 1 = 1480
(v) 1732 × 0 = 0
(vi) 72 × 98 + 72 × 2 = 72 × ( 98 + 2)
(vii) 63 × 126 – 63 × 26 = 63 × (126 – 26)

Ans. (i) Commutative law of multiplication
(ii) Closure property
(iii) Associative law of multiplication
(iv) Multiplicative property of 1
(v) Multiplicative property of 0
(vi) Distributive law of multiplication over addition in whole numbers
(vii) Distributive law of multiplication over subtraction in whole numbers

Q.3. Find the value of each of the following using various properties :
(i) 647 × 13 + 647 × 7
(ii) 8759 × 94 + 8759 × 6
(iii) 7459 × 999 + 7459
(iv) 9870 × 561 – 9870 × 461
(v) 569 × 17 + 569 × 13 + 569 × 70
(vi) 16825 × 16825 – 16825 × 6825

Ans. Using the law of distribution over addition

and subtraction
(i) 647 × 13 + 647 × 7
= 647 × (13 + 7) = 647 × 20
= 12940
(ii) 8759 × 94 + 8759 × 6
= 8759 × (94 + 6) = 8759 × 100
= 875900
(iii) 7459 × 999 + 7459
= 7459 × 999 + 7459 × 1
= 7459 × (999 + 1) = 7459 × 1000
= 7459000
(iv) 9870 × 561 – 9870 × 461
= 9870 × (561 – 461) = 9870 × 100
= 987000

(v) 569 × 17 + 569 × 13 + 569 × 70
= 569 × (17 + 13 + 70) = 569 × 100
= 56900

(vi) 16825 × 16825 – 16825 × 6825
= 16825 × (16825 – 6825)
= 16825 × 10000 = 168250000

Q.4. Determine each of the following products by suitable rearrangements :

(i) 2 × 1658 × 50

(ii) 4 × 927 × 25

(iii) 625 × 20 × 8 × 50

(iv) 574 × 625 × 16

(v) 250 × 60 × 50 × 8

(vi) 8 × 125 × 40 × 25

Ans. (i) 2 × 1658 × 50 = 1658 × (2 × 50)
(Associative law of multiplication)
1658 × 100 = 165800
(ii) 4 × 927 × 25 = 927 × (4 × 25)

(Associative law of multiplication)
= 927 × 100 = 92700

(iii) 625 × 20 × 8 × 50
(By associative law of multiplication)
(625 × 8) × (20 × 50)
= 5000 × 1000 = 5000000

(iv) 574 × (625 × 16)

= 574 × 10000 = 5740000

(v) 250 × 60 × 50 × 8

= (250 × 8) × (60 × 50)

(By associative law)

= 2000 × 3000 = 6000000

(vi) 8 × 125 × 40 × 25

= (8 × 125) × (40 × 25)

= 1000 × 1000 = 1000000

Q.5. Find each of the following products, using

distributive laws :

(i) 740 × 105
(ii) 245 × 1008

(iii) 947 × 96
(iv) 996 × 367

(v) 472 × 1097
(vi) 580 × 64

(vii) 439 × 997
(viii) 1553 × 198
Ans.
Using distributive law of multiplication over addition or subtraction,

(i) 740 × 105 = 740 × (100 + 5)
= 740 × 100 + 740 × 5
= 74000 + 3700 = 77700

(ii) 245 × 1008 = 245 × (1000 + 8)
= 245 × 1000 + 245 × 8
= 245000 + 1960 = 246960
(iii) 947 × 96 = 947 × (100 – 4)
= 947 × 100 – 947 × 4
= 94700 – 3788 = 90912

(iv) 996 × 367 = 367 × (1000 – 4)
= 367 × 1000 – 367 × 4
= 367000 – 1468 = 365532

(v) 472 × 1097 = 472 × (1100 – 3)
= 472 × 1100 – 472 × 3
= 519200 – 1416 = 517784
(vi) 580 × 64 = 580 × (60 + 4)
= 580 × 60 + 580 × 4
= 34800 + 2320 = 37120
(vii) 439 × 997 = 437 × (1000 – 3)
= 439 × 1000 – 439 × 3
= 439000 – 1317 = 437683
(viii) 1553 × 198 = 1553 × (200 – 2)
= 1553 × 200 – 1553 × 2

= 310600 – 3106 = 307494

Q.6. Find each of the following products, using distributive laws :
(i) 3576 × 9
(ii) 847 × 99
(iii) 2437 × 999
Ans. (i) 3576 × 9 = 3576 × (10 – 1)
= 3576 × 10 – 3576 × 1
= 35760 – 3576 = 32184
(ii) 847 × 99 = 84 × (100 – 1)
= 847 × 100 – 847 × 1
= 84700 – 847 = 83853
(iii) 2437 × 999 = 2437 × (1000 – 1)
= 2437 × 1000 – 2437 × 1
= 2437000 – 2437 = 2434563

Q.7. Find the products :
(i)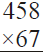
(ii)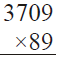
(iii)
(iv)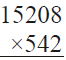
Ans.
(i)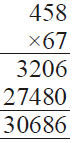

(ii)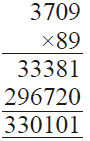

(iii)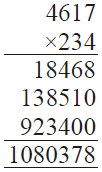

(iv)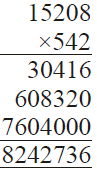


Q.8. Find the product of the largest 3-digit number and the largest 5-digit number.
Ans. Largest 3-digit number = 999
Largest 5-digit number = 99999
Required product = 99999 × 999
= 99999 × (1000 – 1)
= 99999 × 1000 – 99999 × 1
= 99999000 – 99999
= 9,98,99,001

Q.9. A car moves at a uniform speed of 75 km per hour. How much distance will it cover in 98 hours ?
Ans.
Speed of car = 75 km per hour
In 1 hour, distance covered by a car = 75 km
∴ In 98 hours, distance will be covered
= 75 × 98
= 75 × (100 – 2) = 75 × 100 – 75 × 2
= 7500 – 150 = 7350 km

Q.10. A dealer purchased 139 VCRs. If the cost of each set is Rs. 24350, find the cost of all the sets together.
Ans.
Cost of 1 set of VCR = Rs. 24350
Cost of 139 sets of VCR
= Rs. 24350 × 139 = Rs. 3384650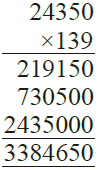


Q.11. A housing society constructed 197 houses. If the cost of construction for each house is Rs. 450000, what is the total cost for all the houses ?
Ans.
Cost of 1 house = Rs. 450000
Cost of 197 houses = Rs. 450000 × 197
= Rs. 450000 × (200 – 3)
= Rs. (450000 × 200 – 450000 × 3)
= Rs. (90000000 – 1350000) = Rs. 88650000

Q.12. 50 chairs and 30 blackboards were purchased for a school. If each chair costs Rs. 1065 and each blackboard costs Rs. 1645, find the total amount of the bill.
Ans.
Cost of each chair = Rs. 1065

∴ Cost of 50 chairs = Rs. 1065 × 50
= Rs. 53250
Cost of each blackboard = Rs. 1645
∴ Cost of 30 blackboards = Rs. 1645 × 30

= Rs. 49350
Total cost of 50 chairs and 30 blackboards
= Rs. 53250 + 49350 = Rs. 102600

Q.13. There are six sections of Class VI in a school and there are 45 students in each section. If the monthly charges from each student be Rs. 1650, find the total monthly collection from Class VI.
Ans. Number of students in 1 section = 45
∴ Number of students in 6 sections
= 45 × 6 = 270
Monthly charges of 1 student = Rs. 1650

∴ Total monthly incomes from the class VI

= Rs. 270 × 1650
= Rs. (300 – 30) × 1650
= Rs. (1650 × 300 – 1650 × 30)
= Rs. (495000 – 49500) = Rs. 445500

Q.14. The product of two whole numbers is zero. What do you conclude ?

Ans. Since the product of two whole numbers is zero

∴ From multiplicative property of zero, we conclude that one of the whole numbers is

zero.

Q.15. Fill in the blanks :
(i) Sum of two odd numbers is an ........ number.

(ii) Product of two odd numbers is an ........ number.
(iii) a × a = a ⇒ a = ?

Ans. (i) Sum of two odd numbers is an even number.

(ii) Product of two odd numbers is an odd number.

(iii) a × a = a ⇒ a = 1 as 1 × 1 = 1