Relational Calculus | Database Management System (DBMS) - Computer Science Engineering (CSE) PDF Download
Tuple Relational Calculus (TRC) in DBMS
Tuple Relational Calculus is a non-procedural query language unlike relational algebra. Tuple Calculus provides only the description of the query but it does not provide the methods to solve it. Thus, it explains what to do but not how to do.
In Tuple Calculus, a query is expressed as
{t| P(t)}
where t = resulting tuples,
P(t) = known as Predicate and these are the conditions that are used to fetch t
Thus, it generates set of all tuples t, such that Predicate P(t) is true for t.
P(t) may have various conditions logically combined with OR (∨), AND (∧), NOT(¬).
It also uses quantifiers:
∃ t ∈ r (Q(t)) = ”there exists” a tuple in t in relation r such that predicate Q(t) is true.
∀ t ∈ r (Q(t)) = Q(t) is true “for all” tuples in relation r.
Example:
Table-1: Customer
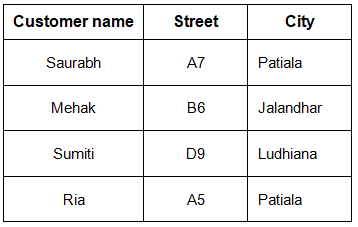 Table-2: Branch
Table-2: Branch
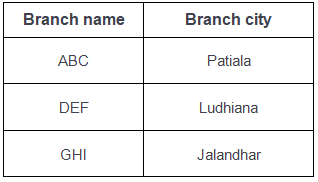
Table-3: Account
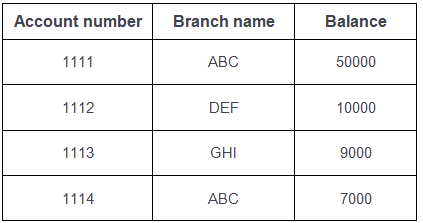 Table-4: Loan
Table-4: Loan
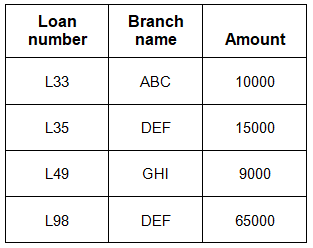 Table-5: Borrower
Table-5: Borrower
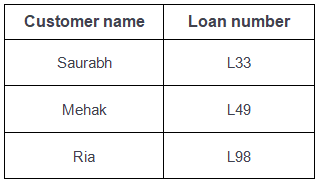
Table-6: Depositor

Queries-1: Find the loan number, branch, amount of loans of greater than or equal to 10000 amount.
{t| t ∈ loan ∧ t[amount]>=10000}
Resulting relation: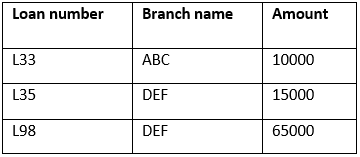 In the above query, t[amount] is known as tupple variable.
In the above query, t[amount] is known as tupple variable.
Queries-2: Find the loan number for each loan of an amount greater or equal to 10000.
{t| ∃ s ∈ loan(t[loan number] = s[loan number]
∧ s[amount]>=10000)}
Resulting relation:
Queries-3: Find the names of all customers who have a loan and an account at the bank.
{t | ∃ s ∈ borrower( t[customer-name] = s[customer-name])
∧ ∃ u ∈ depositor( t[customer-name] = u[customer-name])}
Resulting relation:
Queries-4: Find the names of all customers having a loan at the “ABC” branch.
{t | ∃ s ∈ borrower(t[customer-name] = s[customer-name]
∧ ∃ u ∈ loan(u[branch-name] = “ABC” ∧ u[loan-number] = s[loan-number]))}
Resulting relation:

Domain Relational Calculus in DBMS
Domain Relational Calculus is a non-procedural query language equivalent in power to Tuple Relational Calculus. Domain Relational Calculus provides only the description of the query but it does not provide the methods to solve it. In Domain Relational Calculus, a query is expressed as,
{ < x1, x2, x3, ..., xn > | P (x1, x2, x3, ..., xn ) }
where, < x1, x2, x3, …, xn > represents resulting domains variables and P (x1, x2, x3, …, xn ) represents the condition or formula equivalent to the Predicate calculus.
Predicate Calculus Formula
- Set of all comparison operators
- Set of connectives like and, or, not
- Set of quantifiers
Example:
Table-1: Customer
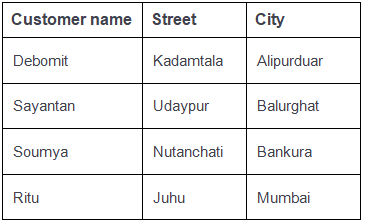
Table-2: Loan
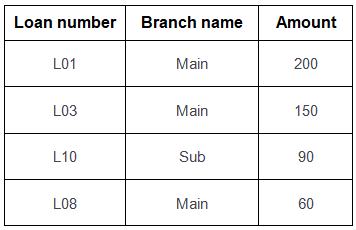
Table-3: Borrower

Query-1: Find the loan number, branch, amount of loans of greater than or equal to 100 amount.
{≺l, b, a≻ | ≺l, b, a≻ ∈ loan ∧ (a ≥ 100)}
Resulting relation:
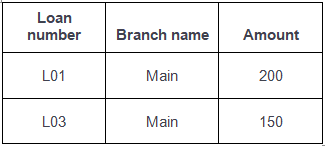
Query-2: Find the loan number for each loan of an amount greater or equal to 150.
{≺l≻ | ∃ b, a (≺l, b, a≻ ∈ loan ∧ (a ≥ 150)}
Resulting relation:

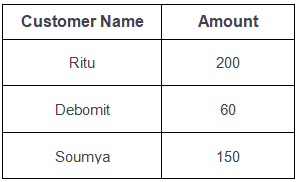
Query-3: Find the names of all customers having a loan at the “Main” branch and find the loan amount.
{≺c, a≻ | ∃ l (≺c, l≻ ∈ borrower ∧ ∃ b (≺l, b, a≻ ∈ loan ∧ (b = “Main”)))}
Resulting relation:
Note: The domain variables those will be in resulting relation must appear before | within ≺ and ≻ and all the domain variables must appear in which order they are in original relation or table.
|
62 videos|99 docs|35 tests
|
FAQs on Relational Calculus - Database Management System (DBMS) - Computer Science Engineering (CSE)
| 1. What is Tuple Relational Calculus (TRC) in DBMS? |  |
| 2. How does Tuple Relational Calculus differ from Domain Relational Calculus? |  |
| 3. What are the advantages of using Tuple Relational Calculus? |  |
| 4. Can Tuple Relational Calculus be used for complex queries? |  |
| 5. Is Tuple Relational Calculus widely used in practice? |  |
















