Lossless Decomposition | Database Management System (DBMS) - Computer Science Engineering (CSE) PDF Download
Lossless Join and Dependency Preserving Decomposition
Decomposition of a relation is done when a relation in relational model is not in appropriate normal form. Relation R is decomposed into two or more relations if decomposition is lossless join as well as dependency preserving.
Lossless Join Decomposition
If we decompose a relation R into relations R1 and R2,
- Decomposition is lossy if R1 ⋈ R2 ⊃ R
- Decomposition is lossless if R1 ⋈ R2 = R
To check for lossless join decomposition using FD set, following conditions must hold:
- Union of Attributes of R1 and R2 must be equal to attribute of R. Each attribute of R must be either in R1 or in R2.
Att(R1) U Att(R2) = Att(R) - Intersection of Attributes of R1 and R2 must not be NULL.
Att(R1) ∩ Att(R2) ≠ Φ - Common attribute must be a key for at least one relation (R1 or R2).
Att(R1) ∩ Att(R2) -> Att(R1) or Att(R1) ∩ Att(R2) -> Att(R2)
For Example, A relation R (A, B, C, D) with FD set{A->BC} is decomposed into R1(ABC) and R2(AD) which is a lossless join decomposition as:
- First condition holds true as Att(R1) U Att(R2) = (ABC) U (AD) = (ABCD) = Att(R).
- Second condition holds true as Att(R1) ∩ Att(R2) = (ABC) ∩ (AD) ≠ Φ
- Third condition holds true as Att(R1) ∩ Att(R2) = A is a key of R1(ABC) because A->BC is given.
Dependency Preserving Decomposition
If we decompose a relation R into relations R1 and R2, All dependencies of R either must be a part of R1 or R2 or must be derivable from combination of FD’s of R1 and R2.
For Example, A relation R (A, B, C, D) with FD set{A->BC} is decomposed into R1(ABC) and R2(AD) which is dependency preserving because FD A->BC is a part of R1(ABC).
GATE Question
Q. Consider a schema R(A,B,C,D) and functional dependencies A->B and C->D. Then the decomposition of R into R1(AB) and R2(CD) is [GATE-CS-2001]
(a) dependency preserving and lossless join
(b) lossless join but not dependency preserving
(c) dependency preserving but not lossless join
(d) not dependency preserving and not lossless join
Ans: (c)
Solution: For lossless join decomposition, these three conditions must hold true:
- Att(R1) U Att(R2) = ABCD = Att(R)
- Att(R1) ∩ Att(R2) = Φ, which violates the condition of lossless join decomposition.
Hence the decomposition is not lossless.
For dependency preserving decomposition,
A -> B can be ensured in R1(AB) and C->D can be ensured in R2(CD). Hence it is dependency preserving decomposition.
So, the correct option is C.
Dependency Preservation
A Decomposition D = { R1, R2, R3….Rn } of R is dependency preserving wrt a set F of Functional dependency if
(F1 ∪ F2 ∪ … ∪ Fm)+ = F+.
Consider a relation R
R ---> F{...with some functional dependency(FD)....}
R is decomposed or divided into R1 with FD { f1 } and R2 with { f2 }, then
there can be three cases:
f1 U f2 = F -----> Decomposition is dependency preserving.
f1 U f2 is a subset of F -----> Not Dependency preserving.
f1 U f2 is a super set of F -----> This case is not possible.
Problem: Let a relation R (A, B, C, D ) and functional dependency {AB –> C, C –> D, D –> A}. Relation R is decomposed into R1( A, B, C) and R2(C, D). Check whether decomposition is dependency preserving or not.
Solution:
R1(A, B, C) and R2(C, D)
Let us find closure of F1 and F2
To find closure of F1, consider all combination of
ABC. i.e., find closure of A, B, C, AB, BC and AC
Note: ABC is not considered as it is always ABC
closure(A) = { A } // Trivial
closure(B) = { B } // Trivial
closure(C) = {C, A, D} but D can't be in closure as D is not present R1.
= {C, A}
C--> A // Removing C from right side as it is trivial attribute
closure(AB) = {A, B, C, D}
= {A, B, C}
AB --> C // Removing AB from right side as these are trivial attributes
closure(BC) = {B, C, D, A}
= {A, B, C}
BC --> A // Removing BC from right side as these are trivial attributes
closure(AC) = {A, C, D}
AC --> D // Removing AC from right side as these are trivial attributes
F1 {C--> A, AB --> C, BC --> A}.
Similarly F2 { C--> D }
In the original Relation Dependency { AB --> C , C --> D , D --> A}.
AB --> C is present in F1.
C --> D is present in F2.
D --> A is not preserved.
F1 U F2 is a subset of F. So given decomposition is not dependency preserving.
Finding Attribute Closure and Candidate Keys using Functional Dependencies
What is Functional Dependency?
A functional dependency X->Y in a relation holds if two tuples having same value for X also have same value for Y i.e X uniquely determines Y.
In EMPLOYEE relation given in Table 1,
- FD E-ID->E-NAME holds because for each E-ID, there is a unique value of E-NAME.
- FD E-ID->E-CITY and E-CITY->E-STATE also holds.
- FD E-NAME->E-ID does not hold because E-NAME ‘John’ is not uniquely determining E-ID. There are 2 E-IDs corresponding to John (E001 and E003).
EMPLOYEE
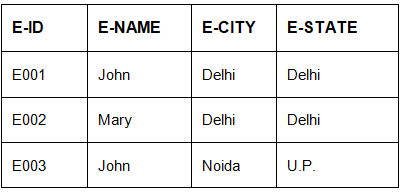 Table 1
Table 1
The FD set for EMPLOYEE relation given in Table 1 are:
{E-ID->E-NAME, E-ID->E-CITY, E-ID->E-STATE, E-CITY->E-STATE}
Trivial versus Non-Trivial Functional Dependency: A trivial functional dependency is the one which will always hold in a relation.
X->Y will always hold if X ⊇ Y
In the example given above, E-ID, E-NAME->E-ID is a trivial functional dependency and will always hold because {E-ID,E-NAME} ⊃ {E-ID}. You can also see from the table that for each value of {E-ID, E-NAME}, value of E-ID is unique, so {E-ID, E-NAME} functionally determines E-ID.
If a functional dependency is not trivial, it is called Non-Trivial Functional Dependency. Non-Trivial functional dependency may or may not hold in a relation. e.g; E-ID->E-NAME is a non-trivial functional dependency which holds in the above relation.
Properties of Functional Dependencies
Let X, Y, and Z are sets of attributes in a relation R. There are several properties of functional dependencies which always hold in R also known as Armstrong Axioms.
- Reflexivity: If Y is a subset of X, then X → Y. e.g.; Let X represents {E-ID, E-NAME} and Y represents {E-ID}. {E-ID, E-NAME}->E-ID is true for the relation.
- Augmentation: If X → Y, then XZ → YZ. e.g.; Let X represents {E-ID}, Y represents {E-NAME} and Z represents {E-CITY}. As {E-ID}->E-NAME is true for the relation, so { E-ID,E-CITY}->{E-NAME,E-CITY} will also be true.
- Transitivity: If X → Y and Y → Z, then X → Z. e.g.; Let X represents {E-ID}, Y represents {E-CITY} and Z represents {E-STATE}. As {E-ID} ->{E-CITY} and {E-CITY}->{E-STATE} is true for the relation, so { E-ID }->{E-STATE} will also be true.
- Attribute Closure: The set of attributes that are functionally dependent on the attribute A is called Attribute Closure of A and it can be represented as A+.
Steps to Find the Attribute Closure of A
Q. Given FD set of a Relation R, The attribute closure set S be the set of A
- Add A to S.
- Recursively add attributes which can be functionally determined from attributes of the set S until done.
From Table 1, FDs are
Given R(E-ID, E-NAME, E-CITY, E-STATE)
FDs = { E-ID->E-NAME, E-ID->E-CITY, E-ID->E-STATE, E-CITY->E-STATE }
The attribute closure of E-ID can be calculated as:
- Add E-ID to the set {E-ID}
- Add Attributes which can be derived from any attribute of set. In this case, E-NAME and E-CITY, E-STATE can be derived from E-ID. So these are also a part of closure.
- As there is one other attribute remaining in relation to be derived from E-ID. So result is: (E-ID)+ = {E-ID, E-NAME, E-CITY, E-STATE }
Similarly,
(E-NAME)+ = {E-NAME}
(E-CITY)+ = {E-CITY, E_STATE}
Q. Find the attribute closures of given FDs R(ABCDE) = {AB->C, B->D, C->E, D->A} To find (B)+ ,we will add attribute in set using various FD which has been shown in table below.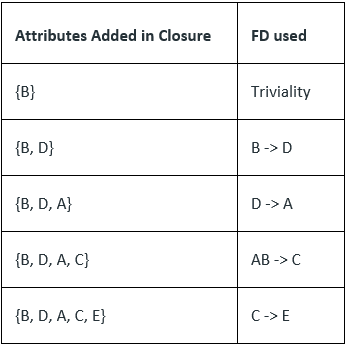
- We can find (C, D)+ by adding C and D into the set (triviality) and then E using(C -> E) and then A using (D -> A) and set becomes.
(C, D)+ = {C, D, E, A} - Similarly we can find (B, C)+ by adding B and C into the set (triviality) and then D using (B -> D) and then E using (C -> E) and then A using (D -> A) and set becomes (B, C)+ = {B, C, D, E, A}
Candidate Key
Candidate Key is minimal set of attributes of a relation which can be used to identify a tuple uniquely. For Example, each tuple of EMPLOYEE relation given in Table 1 can be uniquely identified by E-ID and it is minimal as well. So it will be Candidate key of the relation.
A candidate key may or may not be a primary key.
Super Key
Super Key is set of attributes of a relation which can be used to identify a tuple uniquely.For Example, each tuple of EMPLOYEE relation given in Table 1 can be uniquely identified by E-ID or (E-ID, E-NAME) or (E-ID, E-CITY) or (E-ID, E-STATE) or (E_ID, E-NAME, E-STATE) etc. So all of these are super keys of EMPLOYEE relation.
Note: A candidate key is always a super key but vice versa is not true.
|
62 videos|99 docs|35 tests
|
FAQs on Lossless Decomposition - Database Management System (DBMS) - Computer Science Engineering (CSE)
| 1. What is lossless decomposition? |  |
| 2. Why is lossless decomposition important in database design? |  |
| 3. How does lossless decomposition differ from lossy decomposition? |  |
| 4. What are the advantages of lossless decomposition? |  |
| 5. Can lossless decomposition be applied to any relation? |  |





















