The Scalar Product | NCERT on your Fingertips 2025-2026 Edition - NEET PDF Download

Velocity, displacement, force and acceleration are different types of vectors. Is there a way to find the effect of one vector on another? Can vectors operate in different directions and still affect each other? The answer lies in the Scalar product. An operation that reduces two or more vectors into a Scalar quantity! Let us see more!

What is a Scalar Quantity?

Before we learn about the Scalar product of two vectors, let’s refresh what we have already learned about the difference between a vector quantity and a scalar quantity. Scalar quantity is one dimensional and is described by its magnitude alone.  For example, distance, speed, mass etc.
Vector quantities, on the other hand, have a magnitude as well as a direction.  For example displacement, velocity, acceleration, force etc.  Some vector quantities are effectively the directional values of their corresponding scalar quantities. For example,  displacement, effectively, is the distance in a particular direction.  Vector quantities are expressed with an arrow above the appointed symbols. For example, displacement is expressed as 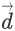 The following image explains the difference between distance, a scalar quantity, and displacement, a vector quantity: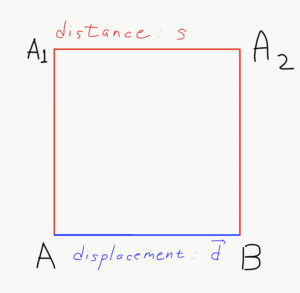

In the above diagram, if we take the square AA1A2B and assume it’s side as 5m, then the object travelling the red path has travelled a distance of 15 meters.  But, the displacement of the said object is only 5 meters in the direction of A to B. Similarly, if we assume that the same object has finished the traversing the red path in one second, then, the object’s speed is 15 m/s. But, the velocity of the said object is only 5 m/s.
Now, in Physics, from time to time, we need to multiply two vector quantities. Some of these multiplications require a scalar product. For example, Work is a scalar quantity and is a product of Force and Displacement. Here, we will learn how to derive a scalar quantity as a product of two vectors, and, how these multiplications hold various laws of mathematics.

Scalar Product of Two Vectors

Let’s consider two vector quantities A and B. We denote them as follows: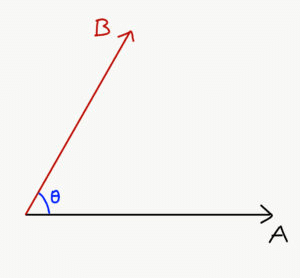

Their scalar product is A dot B.  It is defined as:
A.B = |A| |B| cosθ
Where, θ is the smaller angle between the vector A and vector B. An important reason to define it this way is that |B|cosθ is the projection of the vector B on the vector A. The projections can be understood from the following images: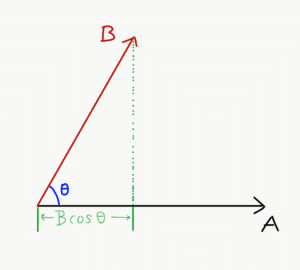

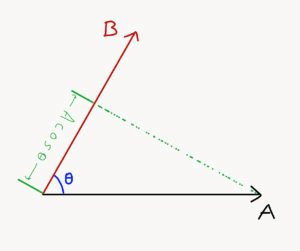
Since, A(Bcosθ) = B(Acosθ), we can say that
A.B = B.A
Hence, we say that the scalar product follows the commutative law. Similarly, the scalar product also follows the distributive law:
A.(B+C) = A.B + A.C
Now, let us assume three unit vectors, i, j and k, along with the three mutually perpendicular axes X, Y and Z respectively.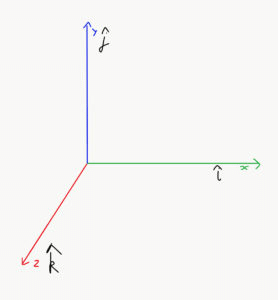

As cos (0) = 1, we have: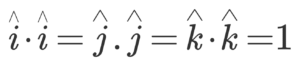

Also since the cosine of 90 degrees is zero, we have: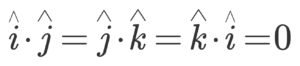

These two findings will help us deduce the scalar product of two vectors in three dimensions. Now, let’s assume two vectors alongside the above three axes: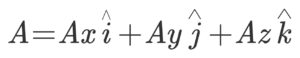


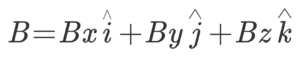
So their scalar product will be,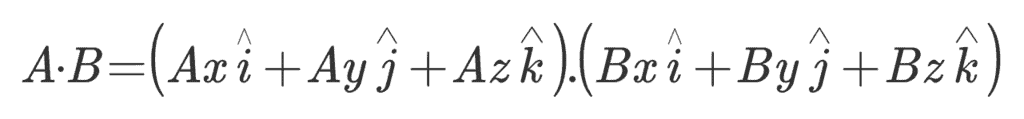

Hence,
A.B = A_xB_x + A_yB_y + A_zB_z  
Similarly, A² or A.A =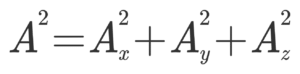

In Physics many quantities like work are represented by the scalar product of two vectors. The scalar product or the dot product is a mathematical operation that combines two vectors and results in a scalar. The magnitude of the scalar depends upon the magnitudes of the combining vectors and the inclination between them.

Solved Examples For You

Q: Let’s find the angle between force and the displacement; where, F = (2i + 3j + 4k) and d = (4i + 2j + 3k).
Solution: We already know that,  A.B = A_xB_x + A_yB_y + A_zB_z
Hence, F.d = F_xd_x + F_yd_y + F_zd_z = 2*4 + 3*2 + 4*3 = 26 units 
Also, F.d = F dcosθ
Now, F² = 2² + 3² + 4² = √29 units 
Similarly, d² = 4² + 2² + 3² = √29 units 
Hence, F d cosθ = 26 
Then, cosθ = 26/(F d) = 26/(√29 × √29) = 26/29, which gives cosθ = 0.89 or θ = cos^-1(0.89)