Towers of Hanoi | Programming and Data Structures - Computer Science Engineering (CSE) PDF Download
Tower of Hanoi, is a mathematical puzzle which consists of three towers (pegs) and more than one rings is as depicted −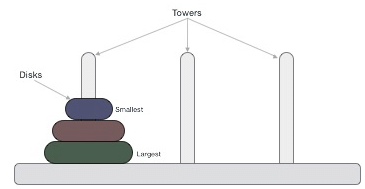 These rings are of different sizes and stacked upon in an ascending order, i.e. the smaller one sits over the larger one. There are other variations of the puzzle where the number of disks increase, but the tower count remains the same.
These rings are of different sizes and stacked upon in an ascending order, i.e. the smaller one sits over the larger one. There are other variations of the puzzle where the number of disks increase, but the tower count remains the same.
Rules
The mission is to move all the disks to some another tower without violating the sequence of arrangement. A few rules to be followed for Tower of Hanoi are −
- Only one disk can be moved among the towers at any given time.
- Only the "top" disk can be removed.
- No large disk can sit over a small disk.
Following is an animated representation of solving a Tower of Hanoi puzzle with three disks.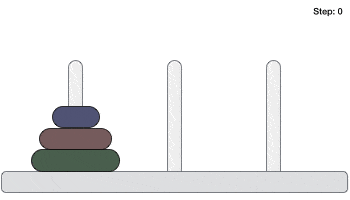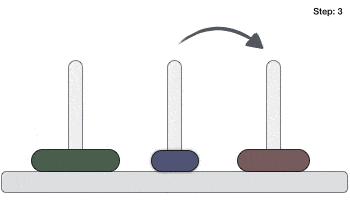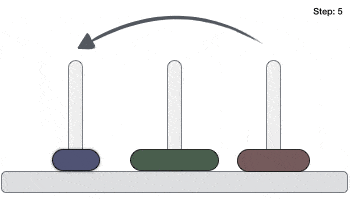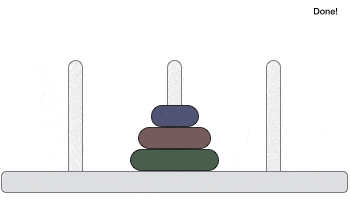
Tower of Hanoi puzzle with n disks can be solved in minimum 2n−1 steps. This presentation shows that a puzzle with 3 disks has taken 23 - 1 = 7 steps.
Algorithm
- To write an algorithm for Tower of Hanoi, first we need to learn how to solve this problem with lesser amount of disks, say → 1 or 2. We mark three towers with name, source, destination and aux (only to help moving the disks). If we have only one disk, then it can easily be moved from source to destination peg.
we have 2 disks − - First, we move the smaller (top) disk to aux peg.
- Then, we move the larger (bottom) disk to destination peg.
- And finally, we move the smaller disk from aux to destination peg.
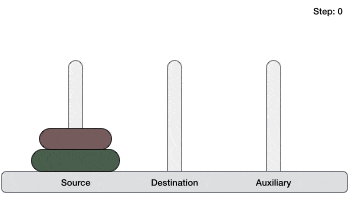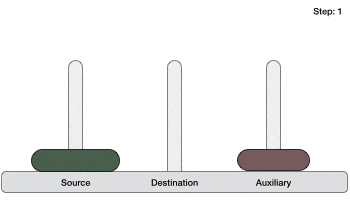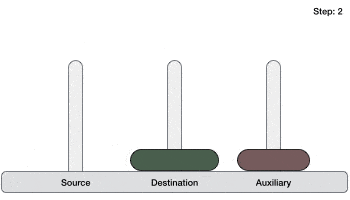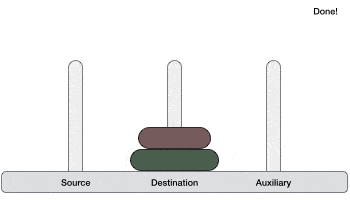
So now, we are in a position to design an algorithm for Tower of Hanoi with more than two disks. We divide the stack of disks in two parts. The largest disk (nth disk) is in one part and all other (n-1) disks are in the second part.
Our ultimate aim is to move disk n from source to destination and then put all other (n1) disks onto it. We can imagine to apply the same in a recursive way for all given set of disks.
The steps to follow are:
Step 1: Move n-1 disks from source to aux
Step 2: Move nth disk from source to dest
Step 3: Move n-1 disks from aux to dest
A recursive algorithm for Tower of Hanoi can be driven as follows:
START
Procedure Hanoi(disk, source, dest, aux)
IF disk == 1, THEN
move disk from source to dest ELSE
Hanoi(disk - 1, source, aux, dest) // Step 1
move disk from source to dest // Step 2
Hanoi(disk - 1, aux, dest, source) // Step 3
END IF
END Procedure
STOP
|
159 docs|30 tests
|
FAQs on Towers of Hanoi - Programming and Data Structures - Computer Science Engineering (CSE)
| 1. What is the Towers of Hanoi problem? |  |
| 2. How many moves are required to solve the Towers of Hanoi problem with n disks? |  |
| 3. What are the rules for solving the Towers of Hanoi problem? |  |
| 4. What is the recursive algorithm to solve the Towers of Hanoi problem? |  |
| 5. Can the Towers of Hanoi problem be solved iteratively? |  |
















