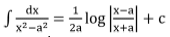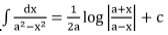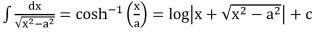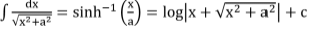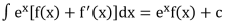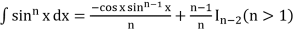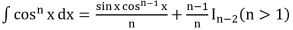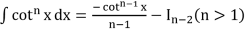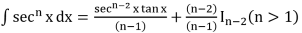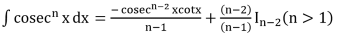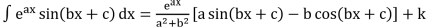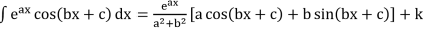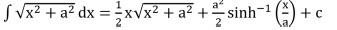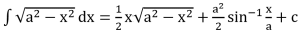Integration - Calculus | Mathematics for NDA PDF Download
Introduction
Let us consider  We observe that the cos x is the derivative function of sin x or we can say that sin x is an anti-derivative (or an integral) of cos x.
We observe that the cos x is the derivative function of sin x or we can say that sin x is an anti-derivative (or an integral) of cos x.
Some Important Integrals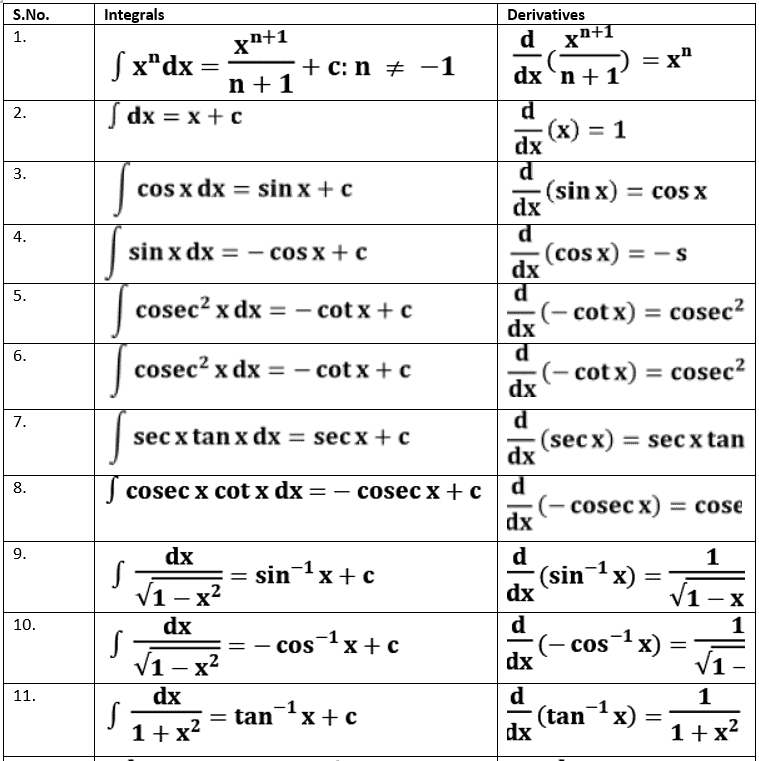
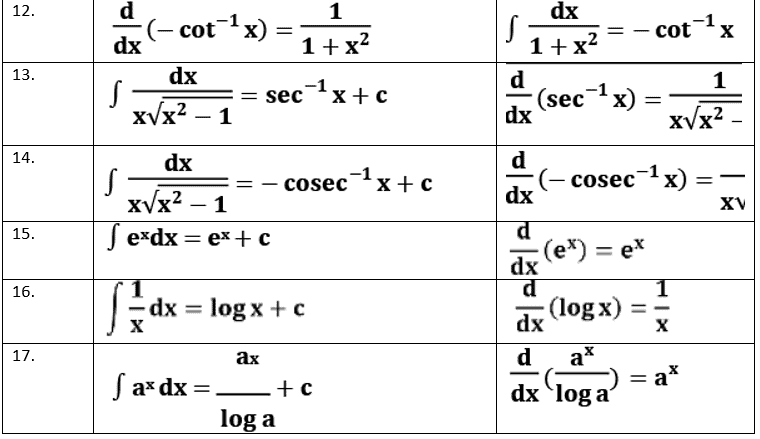
Some Properties of Indefinite Integrals
- ∫ [f(x) + g(x)] dx = ∫f(x)dx + ∫g(x)dx
- ∫kf(x)dx = k∫f(x)dx where k is constant
- ∫f'(ax + b)dx =
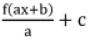
- ∫sinh x dx = cosh x + c
- ∫cosh x dx = sinh x + c
- ∫tanh x dx = log |cosh x| + c
- ∫coth x dx = log |sinh x| + c
- ∫sech x dx = tan-1 |sinh x | + c
- ∫cosec2h x dx = –coth x + c
- ∫cosech x coth x = –cosech x + c
- ∫sech x tanh x dx = –sech x + c
Methods of Integration
- Integration by substitution
- Integration using Trigonometric Identities
- Integration using partial fractions
- Integration by parts
1. Integration by Substitution
The given integral ∫f(x)dx can be transformed into another form by changing the independent variable x to t by substituting x = g(t) Consider, I = ∫f(x)dx
Put, x = g(t) so that dx / dt = g'(t)
dx = g'(t)dt
I = ∫f(x)dx = ∫f(g(t)) g'(t)dt
Example 1:
Integrate the following function, 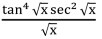
Solution:
Derivative of √x is = 1 / 2√x
We use the substitution √x = t
So, that 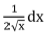 = dt ⇒ dx = 2t dt
= dt ⇒ dx = 2t dt
Thus, 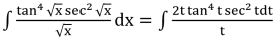
= 2∫tan4 t sec2 t dt
Again we make another substitution tan t = u
sec2 t dt = dx
= 2∫ x4 dx = 2u5/ 5 + c
= 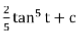
[since u = tan t]
= 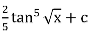
Note:
2. Integration using Trigonometric Identities
The following example can be solved by using trigonometric Identities
Example 2:
∫cos2x dx
Solution:
We know, cos 2x = 2 cos2 x – 1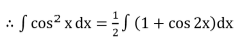
= 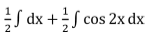
= 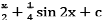
Integrals of Some Particular Functions
To find the integral of type 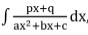 , where p,q,a,b,c are constants we need to find real numbers A, B such that
, where p,q,a,b,c are constants we need to find real numbers A, B such that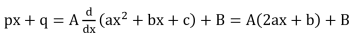
To determine A and B we equate from both sides the coefficients of x and the constant terms.
3. Integration by Partial Fractions
The following example can be solved by using partial fraction method
Example 3:
Find 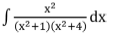
Solution: 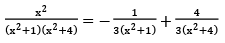
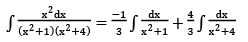
=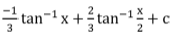
4. Integration by Parts
This can be done by using the given formula
f(x)g(x)dx = f(x)∫g(x)dx – ∫[∫g(x)dx] f'(x)dx
In integration by parts method proper choice of first and second function:
The first function is the word ILATE
I → Inverse Trigonometric
L → Logarithmic
A → Algebraic
T → Trigonometric
E → Exponential
Example 4:
Find the value of ∫x cos x dx
Solution:
Put f(x) = x (first function) and g(x) = cos x (second function) 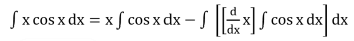
= x sin x – ∫sin x dx
= x sin x + cos x + c
Integrals of Some Particular Functions
Definite Integrals
A real valued function f(x) is continuous on [a, b] then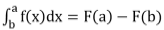 is called definite integral. Geometrically it gives area of finite regions.
is called definite integral. Geometrically it gives area of finite regions.
Properties of Definite Integrals
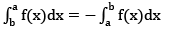
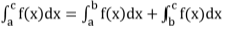
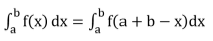
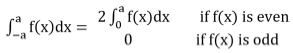
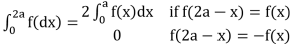

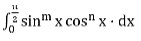
=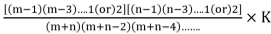 where k = π/2 ; if m and n are even
where k = π/2 ; if m and n are even
= 1 ; otherwise
Example 5:
Find the value of 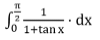
Solution:
Let, I = 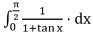
Also, I = 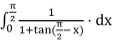 =
= 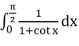 =
= 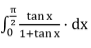

Solving Indefinite Integrals Using Functions
There are two functions which can be used to solve improper indefinite integrals. They are given as
A. Gamma Function
Gamma Function is defined by: 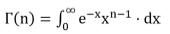
Properties
- Γ(1) = 1
- Γ(2) = 1
- Γ(3) = 2
- Γ(n+1) = nΓ(n) = n!
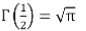
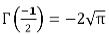
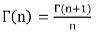
B. β – Function (Beta Function)
It is defined as β(m, n) = 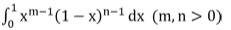
Properties
- β(m, n) = β(n, m)
- β(m, n) =
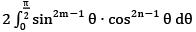
- β(m, n) =
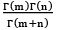
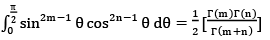
Example 6:
Find the value of 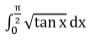
Solution: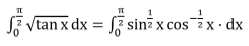
2m - 1 = 1 / 2
⇒ m = 3 / 4
⇒ 2n - 1 = -1 / 2
⇒ n = 1 / 4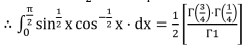
|
290 videos|298 docs|232 tests
|
FAQs on Integration - Calculus - Mathematics for NDA
| 1. What is integration in calculus? |  |
| 2. How is integration different from differentiation in calculus? |  |
| 3. What are the different methods of integration in calculus? |  |
| 4. What are the applications of integration in calculus? |  |
| 5. How can integration be used to find the area between two curves? |  |