Binary Search Tree | Programming and Data Structures - Computer Science Engineering (CSE) PDF Download
Introduction
Binary Search Tree is a node-based binary tree data structure which has the following properties:
- The left subtree of a node contains only nodes with keys lesser than the node’s key.
- The right subtree of a node contains only nodes with keys greater than the node’s key.
- The left and right subtree each must also be a binary search tree.
Binary Search Tree: Search and Insertion
The following is the definition of Binary Search Tree(BST) according to Wikipedia
Binary Search Tree is a node-based binary tree data structure which has the following properties:
- The left subtree of a node contains only nodes with keys lesser than the node’s key.
- The right subtree of a node contains only nodes with keys greater than the node’s key.
- The left and right subtree each must also be a binary search tree.
There must be no duplicate nodes.
The above properties of Binary Search Tree provides an ordering among keys so that the operations like search, minimum and maximum can be done fast. If there is no ordering, then we may have to compare every key to search for a given key.
Searching a key
For searching a value, if we had a sorted array we could have performed a binary search. Let’s say we want to search a number in the array what we do in binary search is we first define the complete list as our search space, the number can exist only within the search space. Now we compare the number to be searched or the element to be searched with the mid element of the search space or the median and if the record being searched is lesser we go searching in the left half else we go searching in the right half, in case of equality we have found the element. In binary search we start with ‘n’ elements in search space and then if the mid element is not the element that we are looking for, we reduce the search space to ‘n/2’ and we go on reducing the search space till we either find the record that we are looking for or we get to only one element in search space and be done with this whole reduction.
Search operation in binary search tree will be very similar. Let’s say we want to search for the number, what we’ll do is we’ll start at the root, and then we will compare the value to be searched with the value of the root if it’s equal we are done with the search if it’s lesser we know that we need to go to the left subtree because in a binary search tree all the elements in the left subtree are lesser and all the elements in the right subtree are greater. Searching an element in the binary search tree is basically this traversal in which at each step we will go either towards left or right and hence in at each step we discard one of the sub-trees. If the tree is balanced, we call a tree balanced if for all nodes the difference between the heights of left and right subtrees is not greater than one, we will start with a search space of ‘n’nodes and when we will discard one of the sub-trees we will discard ‘n/2’ nodes so our search space will be reduced to ‘n/2’ and then in the next step we will reduce the search space to ‘n/4’ and we will go on reducing like this till we find the element or till our search space is reduced to only one node. The search here is also a binary search and that’s why the name binary search tree.
- C++

- Java

- Python

- C#

- Javascript

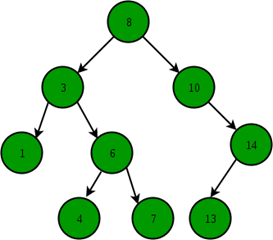
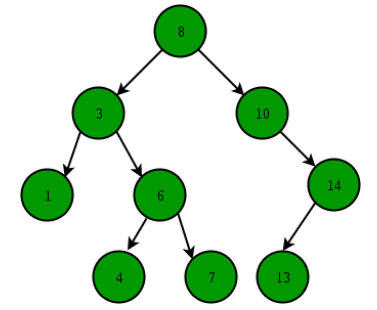
Illustration to search 6 in below tree:
- Start from the root.
- Compare the searching element with root, if less than root, then recurse for left, else recurse for right.
- If the element to search is found anywhere, return true, else return false.

Insertion of a key
A new key is always inserted at the leaf. We start searching a key from the root until we hit a leaf node. Once a leaf node is found, the new node is added as a child of the leaf node.
- C++




- C



- Java




- Python


- C#




Output
20
30
40
50
60
70
80
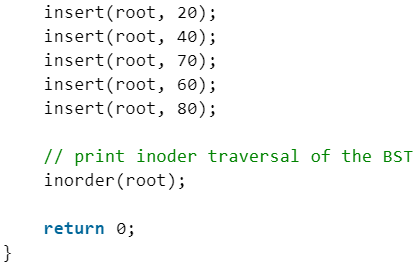
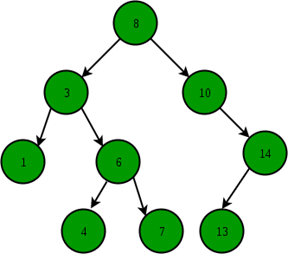
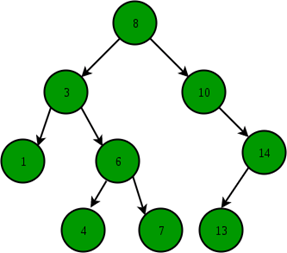
Illustration to insert 2 in below tree:
- Start from the root.
- Compare the inserting element with root, if less than root, then recurse for left, else recurse for right.
- After reaching the end, just insert that node at left(if less than current) else right.

Time Complexity: The worst-case time complexity of search and insert operations is O(h) where h is the height of the Binary Search Tree. In the worst case, we may have to travel from root to the deepest leaf node. The height of a skewed tree may become n and the time complexity of search and insert operation may become O(n).
Insertion using loop:
- Java



Output
10 15 20 30 40 50 60
Some Interesting Facts:
- Inorder traversal of BST always produces sorted output.
- We can construct a BST with only Preorder or Postorder or Level Order traversal. Note that we can always get inorder traversal by sorting the only given traversal.
- Number of unique BSTs with n distinct keys is Catalan Number
Binary Search Tree: Delete
We have discussed BST search and insert operations. In this post, the delete operation is discussed. When we delete a node, three possibilities arise.
- Node to be deleted is the leaf: Simply remove from the tree.

- Node to be deleted has only one child: Copy the child to the node and delete the child

- Node to be deleted has two children: Find inorder successor of the node. Copy contents of the inorder successor to the node and delete the inorder successor. Note that inorder predecessor can also be used.

The important thing to note is, inorder successor is needed only when the right child is not empty. In this particular case, inorder successor can be obtained by finding the minimum value in the right child of the node.
- C++






- C






- Java






- Python





- C#






Output:
Inorder traversal of the given tree
20 30 40 50 60 70 80
Delete 20
Inorder traversal of the modified tree
30 40 50 60 70 80
Delete 30
Inorder traversal of the modified tree
40 50 60 70 80
Delete 50
Inorder traversal of the modified tree
40 60 70 80
Illustration: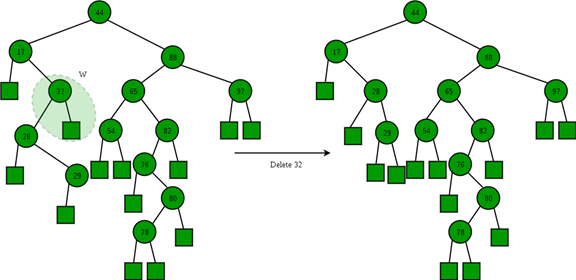
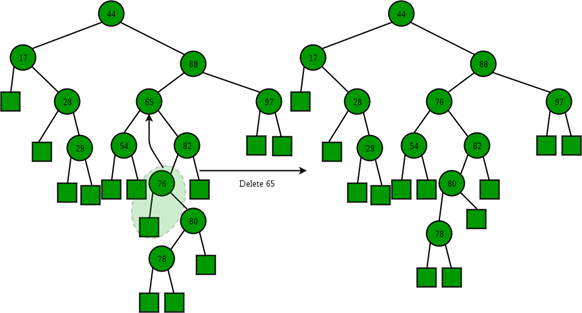 Time Complexity: The worst case time complexity of delete operation is O(h) where h is the height of the Binary Search Tree. In worst case, we may have to travel from the root to the deepest leaf node. The height of a skewed tree may become n and the time complexity of delete operation may become O(n)
Time Complexity: The worst case time complexity of delete operation is O(h) where h is the height of the Binary Search Tree. In worst case, we may have to travel from the root to the deepest leaf node. The height of a skewed tree may become n and the time complexity of delete operation may become O(n)
Optimization to above code for two children case :
In the above recursive code, we recursively call delete() for the successor. We can avoid recursive calls by keeping track of the parent node of the successor so that we can simply remove the successor by making the child of a parent NULL. We know that the successor would always be a leaf node.
- C++






- Java






- Python





Output:
Inorder traversal of the given tree
20 30 40 50 60 70 80
Delete 20
Inorder traversal of the modified tree
30 40 50 60 70 80
Delete 30
Inorder traversal of the modified tree
40 50 60 70 80
Delete 50
Inorder traversal of the modified tree
40 60 70 80
|
119 docs|30 tests
|
FAQs on Binary Search Tree - Programming and Data Structures - Computer Science Engineering (CSE)
| 1. What is a binary search tree? |  |
| 2. How does search operation in a binary search tree work? |  |
| 3. How does insertion operation in a binary search tree work? |  |
| 4. How does deletion operation in a binary search tree work? |  |
| 5. What is the time complexity of search, insertion, and deletion operations in a binary search tree? |  |

|
Explore Courses for Computer Science Engineering (CSE) exam
|

|