Graph Traversal (DFS & BFS) | Programming and Data Structures - Computer Science Engineering (CSE) PDF Download
Breadth First Search or BFS for a Graph
Breadth First Traversal (or Search) for a graph is similar to Breadth First Traversal of a tree (See method 2 of this post). The only catch here is, unlike trees, graphs may contain cycles, so we may come to the same node again. To avoid processing a node more than once, we use a boolean visited array. For simplicity, it is assumed that all vertices are reachable from the starting vertex.
For example, in the following graph, we start traversal from vertex 2. When we come to vertex 0, we look for all adjacent vertices of it. 2 is also an adjacent vertex of 0. If we don’t mark visited vertices, then 2 will be processed again and it will become a non-terminating process. A Breadth First Traversal of the following graph is 2, 0, 3, 1.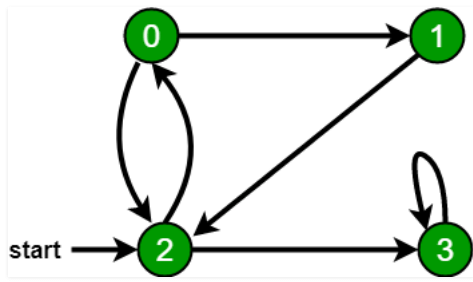
Following are the implementations of simple Breadth First Traversal from a given source.
The implementation uses adjacency list representation of graphs. STL‘s list container is used to store lists of adjacent nodes and queue of nodes needed for BFS traversal.
C++
// Program to print BFS traversal from a given
// source vertex. BFS(int s) traverses vertices
// reachable from s.
#include<iostream>
#include <list>
using namespace std;
// This class represents a directed graph using
// adjacency list representation
class Graph
{
int V; // No. of vertices
// Pointer to an array containing adjacency
// lists
list<int> *adj;
public:
Graph(int V); // Constructor
// function to add an edge to graph
void addEdge(int v, int w);
// prints BFS traversal from a given source s
void BFS(int s);
};
Graph::Graph(int V)
{
this->V = V;
adj = new list<int>[V];
}
void Graph::addEdge(int v, int w)
{
adj[v].push_back(w); // Add w to v’s list.
}
void Graph::BFS(int s)
{
// Mark all the vertices as not visited
bool *visited = new bool[V];
for(int i = 0; i < V; i++)
visited[i] = false;
// Create a queue for BFS
list<int> queue;
// Mark the current node as visited and enqueue it
visited[s] = true;
queue.push_back(s);
// 'i' will be used to get all adjacent
// vertices of a vertex
list<int>::iterator i;
while(!queue.empty())
{
// Dequeue a vertex from queue and print it
s = queue.front();
cout << s << " ";
queue.pop_front();
// Get all adjacent vertices of the dequeued
// vertex s. If a adjacent has not been visited,
// then mark it visited and enqueue it
for (i = adj[s].begin(); i != adj[s].end(); ++i)
{
if (!visited[*i])
{
visited[*i] = true;
queue.push_back(*i);
}
}
}
}
// Driver program to test methods of graph class
int main()
{
// Create a graph given in the above diagram
Graph g(4);
g.addEdge(0, 1);
g.addEdge(0, 2);
g.addEdge(1, 2);
g.addEdge(2, 0);
g.addEdge(2, 3);
g.addEdge(3, 3);
cout << "Following is Breadth First Traversal "
<< "(starting from vertex 2) \n";
g.BFS(2);
return 0;
}
Java
// Java program to print BFS traversal from a given source vertex.
// BFS(int s) traverses vertices reachable from s.
import java.io.*;
import java.util.*;
// This class represents a directed graph using adjacency list
// representation
class Graph
{
private int V; // No. of vertices
private LinkedList<Integer> adj[]; //Adjacency Lists
// Constructor
Graph(int v)
{
V = v;
adj = new LinkedList[v];
for (int i=0; i<v; ++i)
adj[i] = new LinkedList();
}
// Function to add an edge into the graph
void addEdge(int v,int w)
{
adj[v].add(w);
}
// prints BFS traversal from a given source s
void BFS(int s)
{
// Mark all the vertices as not visited(By default
// set as false)
boolean visited[] = new boolean[V];
// Create a queue for BFS
LinkedList<Integer> queue = new LinkedList<Integer>();
// Mark the current node as visited and enqueue it
visited[s]=true;
queue.add(s);
while (queue.size() != 0)
{
// Dequeue a vertex from queue and print it
s = queue.poll();
System.out.print(s+" ");
// Get all adjacent vertices of the dequeued vertex s
// If a adjacent has not been visited, then mark it
// visited and enqueue it
Iterator<Integer> i = adj[s].listIterator();
while (i.hasNext())
{
int n = i.next();
if (!visited[n])
{
visited[n] = true;
queue.add(n);
}
}
}
}
// Driver method to
public static void main(String args[])
{
Graph g = new Graph(4);
g.addEdge(0, 1);
g.addEdge(0, 2);
g.addEdge(1, 2);
g.addEdge(2, 0);
g.addEdge(2, 3);
g.addEdge(3, 3);
System.out.println("Following is Breadth First Traversal "+
"(starting from vertex 2)");
g.BFS(2);
}
}
// This code is contributed by Aakash Hasija
Python3
# Python3 Program to print BFS traversal
# from a given source vertex. BFS(int s)
# traverses vertices reachable from s.
from collections import defaultdict
# This class represents a directed graph
# using adjacency list representation
class Graph:
# Constructor
def __init__(self):
# default dictionary to store graph
self.graph = defaultdict(list)
# function to add an edge to graph
def addEdge(self,u,v):
self.graph[u].append(v)
# Function to print a BFS of graph
def BFS(self, s):
# Mark all the vertices as not visited
visited = [False] * (max(self.graph) + 1)
# Create a queue for BFS
queue = []
# Mark the source node as
# visited and enqueue it
queue.append(s)
visited[s] = True
while queue:
# Dequeue a vertex from
# queue and print it
s = queue.pop(0)
print (s, end = " ")
# Get all adjacent vertices of the
# dequeued vertex s. If a adjacent
# has not been visited, then mark it
# visited and enqueue it
for i in self.graph[s]:
if visited[i] == False:
queue.append(i)
visited[i] = True
# Driver code
# Create a graph given in
# the above diagram
g = Graph()
g.addEdge(0, 1)
g.addEdge(0, 2)
g.addEdge(1, 2)
g.addEdge(2, 0)
g.addEdge(2, 3)
g.addEdge(3, 3)
print ("Following is Breadth First Traversal"
" (starting from vertex 2)")
g.BFS(2)
# This code is contributed by Neelam Yadav
C#
// C# program to print BFS traversal
// from a given source vertex.
// BFS(int s) traverses vertices
// reachable from s.
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
// This class represents a directed
// graph using adjacency list
// representation
class Graph{
// No. of vertices
private int _V;
//Adjacency Lists
LinkedList<int>[] _adj;
public Graph(int V)
{
_adj = new LinkedList<int>[V];
for(int i = 0; i < _adj.Length; i++)
{
_adj[i] = new LinkedList<int>();
}
_V = V;
}
// Function to add an edge into the graph
public void AddEdge(int v, int w)
{
_adj[v].AddLast(w);
}
// Prints BFS traversal from a given source s
public void BFS(int s)
{
// Mark all the vertices as not
// visited(By default set as false)
bool[] visited = new bool[_V];
for(int i = 0; i < _V; i++)
visited[i] = false;
// Create a queue for BFS
LinkedList<int> queue = new LinkedList<int>();
// Mark the current node as
// visited and enqueue it
visited[s] = true;
queue.AddLast(s);
while(queue.Any())
{
// Dequeue a vertex from queue
// and print it
s = queue.First();
Console.Write(s + " " );
queue.RemoveFirst();
// Get all adjacent vertices of the
// dequeued vertex s. If a adjacent
// has not been visited, then mark it
// visited and enqueue it
LinkedList<int> list = _adj[s];
foreach (var val in list)
{
if (!visited[val])
{
visited[val] = true;
queue.AddLast(val);
}
}
}
}
// Driver code
static void Main(string[] args)
{
Graph g = new Graph(4);
g.AddEdge(0, 1);
g.AddEdge(0, 2);
g.AddEdge(1, 2);
g.AddEdge(2, 0);
g.AddEdge(2, 3);
g.AddEdge(3, 3);
Console.Write("Following is Breadth First " +
"Traversal(starting from " +
"vertex 2)\n");
g.BFS(2);
}
}
// This code is contibuted by anv89
Output:
Following is Breadth First Traversal (starting from vertex 2)
2 0 3 1
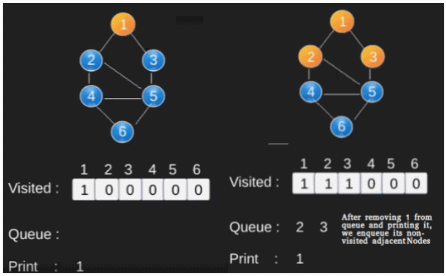
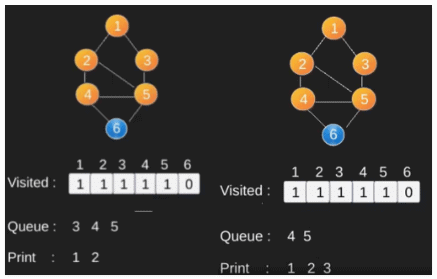
Illustration :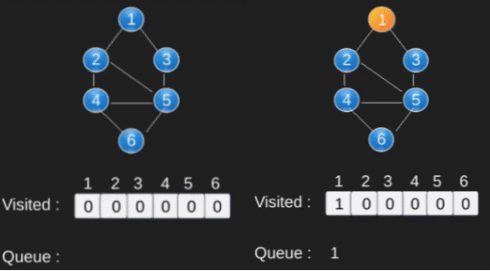
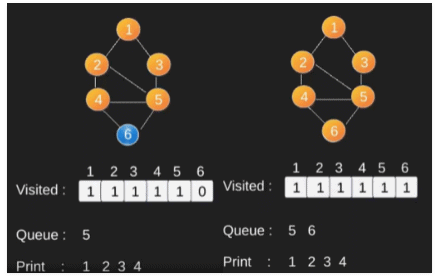
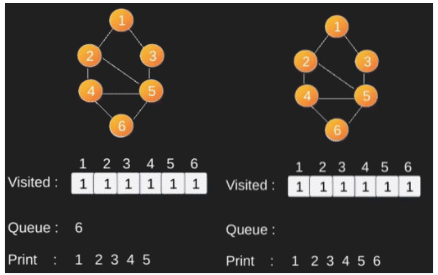
Depth First Search or DFS for a Graph
Depth First Traversal (or Search) for a graph is similar to Depth First Traversal of a tree. The only catch here is, unlike trees, graphs may contain cycles, a node may be visited twice. To avoid processing a node more than once, use a boolean visited array.
Example:
Input: n = 4, e = 6
0 -> 1, 0 -> 2, 1 -> 2, 2 -> 0, 2 -> 3, 3 -> 3
Output: DFS from vertex 1 : 1 2 0 3
Explanation:
DFS Diagram:
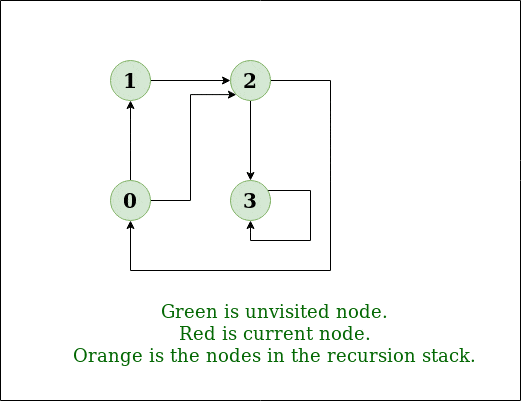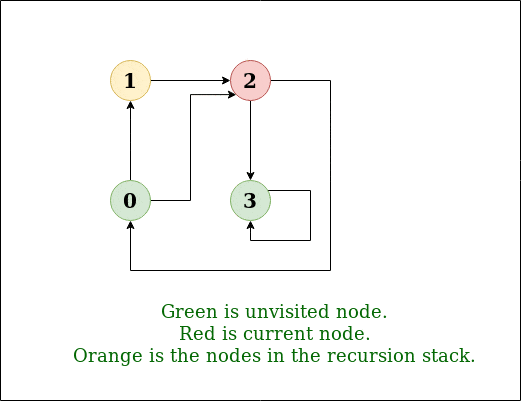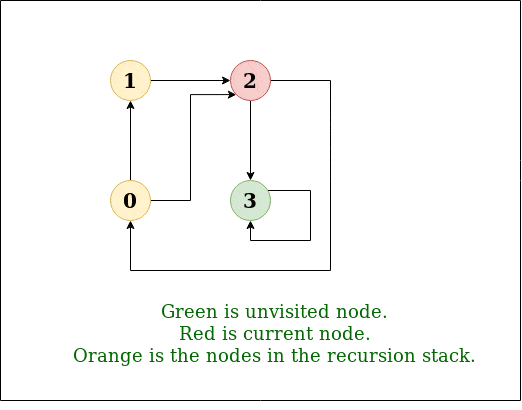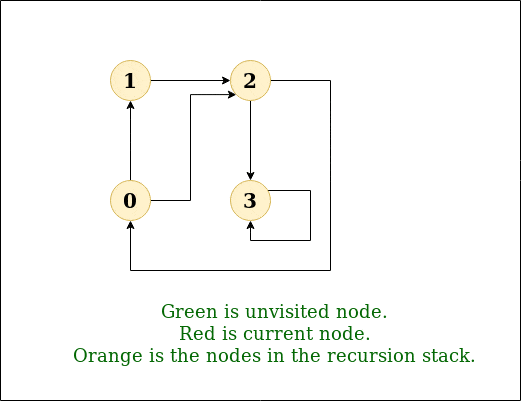
Input: n = 4, e = 6
2 -> 0, 0 -> 2, 1 -> 2, 0 -> 1, 3 -> 3, 1 -> 3
Output: DFS from vertex 2 : 2 0 1 3
Explanation:
DFS Diagram:
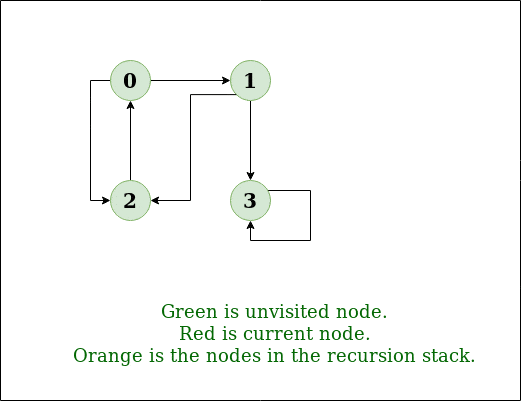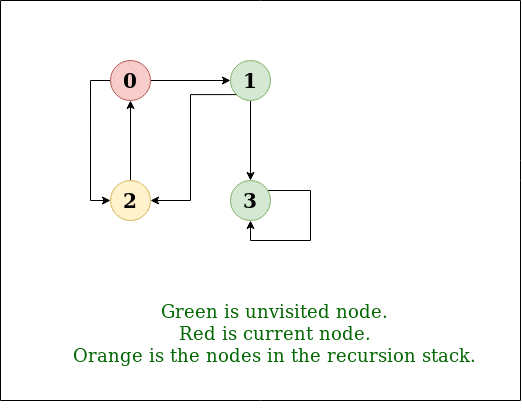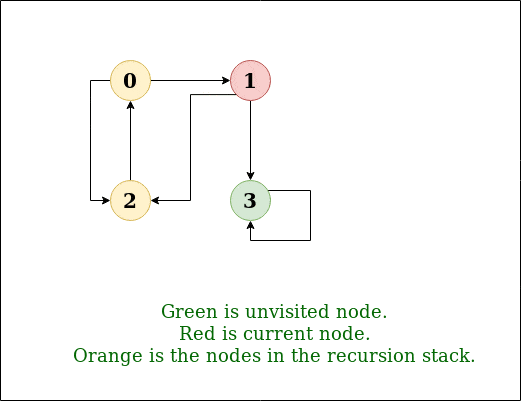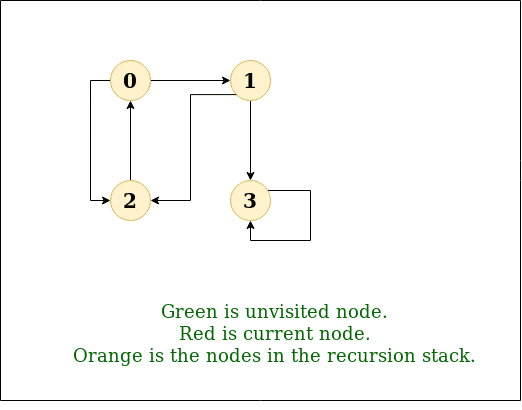
Prerequisites: See this post for all applications of Depth First Traversal.
Following are implementations of simple Depth First Traversal. The C++ implementation uses adjacency list representation of graphs. STL‘s list container is used to store lists of adjacent nodes.
Solution:
- Approach: Depth-first search is an algorithm for traversing or searching tree or graph data structures. The algorithm starts at the root node (selecting some arbitrary node as the root node in the case of a graph) and explores as far as possible along each branch before backtracking. So the basic idea is to start from the root or any arbitrary node and mark the node and move to the adjacent unmarked node and continue this loop until there is no unmarked adjacent node. Then backtrack and check for other unmarked nodes and traverse them. Finally print the nodes in the path.
- Algorithm:
- Create a recursive function that takes the index of node and a visited array.
- Mark the current node as visited and print the node.
- Traverse all the adjacent and unmarked nodes and call the recursive function with index of adjacent node.
Implementation:
C++
// C++ program to print DFS traversal from
// a given vertex in a given graph
#include <bits/stdc++.h>
using namespace std;
// Graph class represents a directed graph
// using adjacency list representation
class Graph
{
public:
map<int, bool> visited;
map<int, list<int>> adj;
// function to add an edge to graph
void addEdge(int v, int w);
// DFS traversal of the vertices
// reachable from v
void DFS(int v);
};
void Graph::addEdge(int v, int w)
{
adj[v].push_back(w); // Add w to v’s list.
}
void Graph::DFS(int v)
{
// Mark the current node as visited and
// print it
visited[v] = true;
cout << v << " ";
// Recur for all the vertices adjacent
// to this vertex
list<int>::iterator i;
for (i = adj[v].begin(); i != adj[v].end(); ++i)
if (!visited[*i])
DFS(*i);
}
// Driver code
int main()
{
// Create a graph given in the above diagram
Graph g;
g.addEdge(0, 1);
g.addEdge(0, 9);
g.addEdge(1, 2);
g.addEdge(2, 0);
g.addEdge(2, 3);
g.addEdge(9, 3);
cout << "Following is Depth First Traversal"
" (starting from vertex 2) \n";
g.DFS(2);
return 0;
}
// improved by Vishnudev C
Java
// Java program to print DFS
//mtraversal from a given given
// graph
import java.io.*;
import java.util.*;
// This class represents a
// directed graph using adjacency
// list representation
class Graph {
private int V; // No. of vertices
// Array of lists for
// Adjacency List Representation
private LinkedList<Integer> adj[];
// Constructor
@SuppressWarnings("unchecked") Graph(int v)
{
V = v;
adj = new LinkedList[v];
for (int i = 0; i < v; ++i)
adj[i] = new LinkedList();
}
// Function to add an edge into the graph
void addEdge(int v, int w)
{
adj[v].add(w); // Add w to v's list.
}
// A function used by DFS
void DFSUtil(int v, boolean visited[])
{
// Mark the current node as visited and print it
visited[v] = true;
System.out.print(v + " ");
// Recur for all the vertices adjacent to this
// vertex
Iterator<Integer> i = adj[v].listIterator();
while (i.hasNext())
{
int n = i.next();
if (!visited[n])
DFSUtil(n, visited);
}
}
// The function to do DFS traversal.
// It uses recursive
// DFSUtil()
void DFS(int v)
{
// Mark all the vertices as
// not visited(set as
// false by default in java)
boolean visited[] = new boolean[V];
// Call the recursive helper
// function to print DFS
// traversal
DFSUtil(v, visited);
}
// Driver Code
public static void main(String args[])
{
Graph g = new Graph(4);
g.addEdge(0, 1);
g.addEdge(0, 2);
g.addEdge(1, 2);
g.addEdge(2, 0);
g.addEdge(2, 3);
g.addEdge(3, 3);
System.out.println(
"Following is Depth First Traversal "
+ "(starting from vertex 2)");
g.DFS(2);
}
}
// This code is contributed by Aakash Hasija
Python3
# Python3 program to print DFS traversal
# from a given given graph
from collections import defaultdict
# This class represents a directed graph using
# adjacency list representation
class Graph:
# Constructor
def __init__(self):
# default dictionary to store graph
self.graph = defaultdict(list)
# function to add an edge to graph
def addEdge(self, u, v):
self.graph[u].append(v)
# A function used by DFS
def DFSUtil(self, v, visited):
# Mark the current node as visited
# and print it
visited.add(v)
print(v, end=' ')
# Recur for all the vertices
# adjacent to this vertex
for neighbour in self.graph[v]:
if neighbour not in visited:
self.DFSUtil(neighbour, visited)
# The function to do DFS traversal. It uses
# recursive DFSUtil()
def DFS(self, v):
# Create a set to store visited vertices
visited = set()
# Call the recursive helper function
# to print DFS traversal
self.DFSUtil(v, visited)
# Driver code
# Create a graph given
# in the above diagram
g = Graph()
g.addEdge(0, 1)
g.addEdge(0, 2)
g.addEdge(1, 2)
g.addEdge(2, 0)
g.addEdge(2, 3)
g.addEdge(3, 3)
print("Following is DFS from (starting from vertex 2)")
g.DFS(2)
# This code is contributed by Neelam Yadav
C#
// C# program to print DFS traversal
// from a given graph
using System;
using System.Collections.Generic;
// This class represents a directed graph
// using adjacency list representation
class Graph {
private int V; // No. of vertices
// Array of lists for
// Adjacency List Representation
private List<int>[] adj;
// Constructor
Graph(int v)
{
V = v;
adj = new List<int>[ v ];
for (int i = 0; i < v; ++i)
adj[i] = new List<int>();
}
// Function to Add an edge into the graph
void AddEdge(int v, int w)
{
adj[v].Add(w); // Add w to v's list.
}
// A function used by DFS
void DFSUtil(int v, bool[] visited)
{
// Mark the current node as visited
// and print it
visited[v] = true;
Console.Write(v + " ");
// Recur for all the vertices
// adjacent to this vertex
List<int> vList = adj[v];
foreach(var n in vList)
{
if (!visited[n])
DFSUtil(n, visited);
}
}
// The function to do DFS traversal.
// It uses recursive DFSUtil()
void DFS(int v)
{
// Mark all the vertices as not visited
// (set as false by default in c#)
bool[] visited = new bool[V];
// Call the recursive helper function
// to print DFS traversal
DFSUtil(v, visited);
}
// Driver Code
public static void Main(String[] args)
{
Graph g = new Graph(4);
g.AddEdge(0, 1);
g.AddEdge(0, 2);
g.AddEdge(1, 2);
g.AddEdge(2, 0);
g.AddEdge(2, 3);
g.AddEdge(3, 3);
Console.WriteLine(
"Following is Depth First Traversal "
+ "(starting from vertex 2)");
g.DFS(2);
Console.ReadKey();
}
}
// This code is contributed by techno2mahi
Output:
Following is Depth First Traversal (starting from vertex 2)
2 0 1 9 3
Complexity Analysis:
- Time complexity: O(V + E), where V is the number of vertices and E is the number of edges in the graph.
- Space Complexity: O(V).
Since, an extra visited array is needed of size V.
Handling Disconnected Graph
- Solution: This will happen by handling a corner case.
The above code traverses only the vertices reachable from a given source vertex. All the vertices may not be reachable from a given vertex as in the case of a Disconnected graph. To do complete DFS traversal of such graphs, run DFS from all unvisited nodes after a DFS.
The recursive function remains the same. - Algorithm:
- Create a recursive function that takes the index of node and a visited array.
- Mark the current node as visited and print the node.
- Traverse all the adjacent and unmarked nodes and call the recursive function with index of adjacent node.
- Run a loop from 0 to number of vertices and check if the node is unvisited in previous DFS then call the recursive function with current node.
Implementation:
C++
// C++ program to print DFS
// traversal for a given given
// graph
#include <bits/stdc++.h>
using namespace std;
class Graph {
// A function used by DFS
void DFSUtil(int v);
public:
map<int, bool> visited;
map<int, list<int>> adj;
// function to add an edge to graph
void addEdge(int v, int w);
// prints DFS traversal of the complete graph
void DFS();
};
void Graph::addEdge(int v, int w)
{
adj[v].push_back(w); // Add w to v’s list.
}
void Graph::DFSUtil(int v)
{
// Mark the current node as visited and print it
visited[v] = true;
cout << v << " ";
// Recur for all the vertices adjacent to this vertex
list<int>::iterator i;
for (i = adj[v].begin(); i != adj[v].end(); ++i)
if (!visited[*i])
DFSUtil(*i);
}
// The function to do DFS traversal. It uses recursive
// DFSUtil()
void Graph::DFS()
{
// Call the recursive helper function to print DFS
// traversal starting from all vertices one by one
for (auto i:adj)
if (visited[i.first] == false)
DFSUtil(i.first);
}
// Driver Code
int main()
{
// Create a graph given in the above diagram
Graph g;
g.addEdge(0, 1);
g.addEdge(0, 9);
g.addEdge(1, 2);
g.addEdge(2, 0);
g.addEdge(2, 3);
g.addEdge(9, 3);
cout << "Following is Depth First Traversal \n";
g.DFS();
return 0;
}
//improved by Vishnudev C
Java
// Java program to print DFS
// traversal from a given given
// graph
import java.io.*;
import java.util.*;
// This class represents a
// directed graph using adjacency
// list representation
class Graph {
private int V; // No. of vertices
// Array of lists for
// Adjacency List Representation
private LinkedList<Integer> adj[];
// Constructor
@SuppressWarnings("unchecked") Graph(int v)
{
V = v;
adj = new LinkedList[v];
for (int i = 0; i < v; ++i)
adj[i] = new LinkedList();
}
// Function to add an edge into the graph
void addEdge(int v, int w)
{
adj[v].add(w); // Add w to v's list.
}
// A function used by DFS
void DFSUtil(int v, boolean visited[])
{
// Mark the current node as visited and print it
visited[v] = true;
System.out.print(v + " ");
// Recur for all the vertices adjacent to this
// vertex
Iterator<Integer> i = adj[v].listIterator();
while (i.hasNext()) {
int n = i.next();
if (!visited[n])
DFSUtil(n, visited);
}
}
// The function to do DFS traversal. It uses recursive
// DFSUtil()
void DFS()
{
// Mark all the vertices as not visited(set as
// false by default in java)
boolean visited[] = new boolean[V];
// Call the recursive helper function to print DFS
// traversal starting from all vertices one by one
for (int i = 0; i < V; ++i)
if (visited[i] == false)
DFSUtil(i, visited);
}
// Driver Code
public static void main(String args[])
{
Graph g = new Graph(4);
g.addEdge(0, 1);
g.addEdge(0, 2);
g.addEdge(1, 2);
g.addEdge(2, 0);
g.addEdge(2, 3);
g.addEdge(3, 3);
System.out.println(
"Following is Depth First Traversal");
g.DFS();
}
}
// This code is contributed by Aakash Hasija
Python
# Python program to print DFS
# traversal for complete graph
from collections import defaultdict
# This class represents a
# directed graph using adjacency
# list representation
class Graph:
# Constructor
def __init__(self):
# default dictionary to store graph
self.graph = defaultdict(list)
# function to add an edge to graph
def addEdge(self, u, v):
self.graph[u].append(v)
# A function used by DFS
def DFSUtil(self, v, visited):
# Mark the current node as visited and print it
visited.add(v)
print v,
# Recur for all the vertices adjacent to
# this vertex
for neighbour in self.graph[v]:
if neighbour not in visited:
self.DFSUtil(neighbour, visited)
# The function to do DFS traversal. It uses
# recursive DFSUtil()
def DFS(self):
# Create a set to store all visited vertices
visited = set()
# Call the recursive helper function to print
# DFS traversal starting from all vertices one
# by one
for vertex in list(self.graph):
if vertex not in visited:
self.DFSUtil(vertex, visited)
# Driver code
# Create a graph given in the above diagram
g = Graph()
g.addEdge(0, 1)
g.addEdge(0, 2)
g.addEdge(1, 2)
g.addEdge(2, 0)
g.addEdge(2, 3)
g.addEdge(3, 3)
print "Following is Depth First Traversal"
g.DFS()
# This code is contributed by Neelam Yadav
C#
// C# program to print DFS
// traversal from a given given
// graph
using System;
using System.Collections.Generic;
// This class represents a
// directed graph using adjacency
// list representation
public class Graph {
private int V; // No. of vertices
// Array of lists for
// Adjacency List Representation
private List<int>[] adj;
// Constructor
Graph(int v)
{
V = v;
adj = new List<int>[ v ];
for (int i = 0; i < v; ++i)
adj[i] = new List<int>();
}
// Function to add an edge into the graph
void addEdge(int v, int w)
{
adj[v].Add(w); // Add w to v's list.
}
// A function used by DFS
void DFSUtil(int v, bool[] visited)
{
// Mark the current
// node as visited and print it
visited[v] = true;
Console.Write(v + " ");
// Recur for all the
// vertices adjacent to this
// vertex
foreach(int i in adj[v])
{
int n = i;
if (!visited[n])
DFSUtil(n, visited);
}
}
// The function to do
// DFS traversal. It uses recursive
// DFSUtil()
void DFS()
{
// Mark all the vertices as not visited(set as
// false by default in java)
bool[] visited = new bool[V];
// Call the recursive helper
// function to print DFS
// traversal starting from
// all vertices one by one
for (int i = 0; i < V; ++i)
if (visited[i] == false)
DFSUtil(i, visited);
}
// Driver code
public static void Main(String[] args)
{
Graph g = new Graph(4);
g.addEdge(0, 1);
g.addEdge(0, 2);
g.addEdge(1, 2);
g.addEdge(2, 0);
g.addEdge(2, 3);
g.addEdge(3, 3);
Console.WriteLine(
"Following is Depth First Traversal");
g.DFS();
}
}
// This code is contributed by PrinciRaj1992
Output:
Following is Depth First Traversal
0 1 2 3
Complexity Analysis:
- Time complexity: O(V + E), where V is the number of vertices and E is the number of edges in the graph.
- Space Complexity :O(V).
Since an extra visited array is needed of size V.
|
158 docs|31 tests
|
FAQs on Graph Traversal (DFS & BFS) - Programming and Data Structures - Computer Science Engineering (CSE)
| 1. What is the difference between Breadth First Search (BFS) and Depth First Search (DFS) for a graph? |  |
| 2. When should I use Breadth First Search (BFS) for graph traversal? |  |
| 3. When should I use Depth First Search (DFS) for graph traversal? |  |
| 4. What is the time complexity of Breadth First Search (BFS) and Depth First Search (DFS) for a graph? |  |
| 5. Can BFS or DFS be used to find the shortest path in a weighted graph? |  |
















