Trigonometric Ratios of Some Specific Angles | Mathematics for SSS 1 PDF Download
Trigonometry is all about triangles or to more precise about the relation between the angles and sides of a right-angled triangle. In this article we will be discussing about the ratio of sides of a right-angled triangle respect to its acute angle called trigonometric ratios of the angle and find the trigonometric ratios of specific angles: 0°, 30°, 45°, 60°, and 90°.
Consider the following triangle: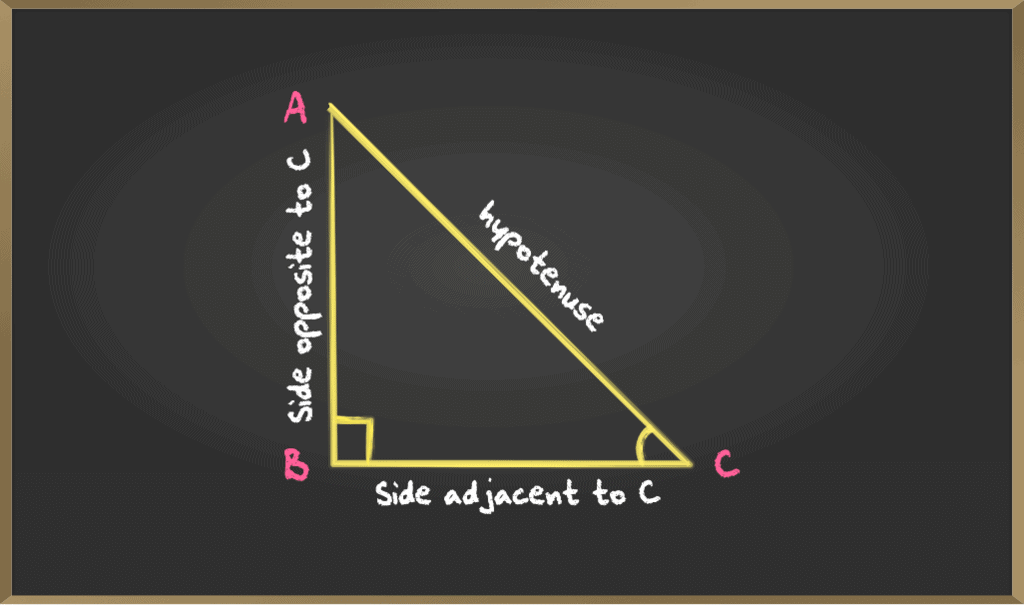
The side BA is opposite to angle ∠BCA so we call BA the opposite side to ∠C and AC is the hypotenuse, the other side BC is the adjacent side to ∠C.
Trigonometric Ratios of angle C
Sine: Sine of ∠C is the ratio between BA and AC that is the ratio between the side opposite to C and the hypotenuse.
Sin C = BA/AC
Cosine: Cosine of ∠C is the ratio between BC and AC that is the ratio between the side adjacent to C and the hypotenuse.
Cos C = BC/AC
Tangent: Tangent of ∠C is the ratio between BA and BC that is the ratio between the side opposite and adjacent to C
Tan C = BA/BC
Cosecant: Cosecant of ∠C is the reciprocal of sin C that is the ratio between the hypotenuse and the side opposite to C.
csc C = BA/AC
Secant: Secant of ∠C is the reciprocal of cos C that is the ratio between the hypotenuse and the side adjacent to C.
sec C = BA/AC
Cotangent: Cotangent of ∠C is the reciprocal of tan C that is the ratio between the side adjacent to C and side opposite to C.
Cot C = BA/AC
Finding trigonometric ratios for angle 0°, 30°, 45°, 60°, 90°
A. For angles 0° and 90°
If an angle A = 0° then the length of the opposite side would be zero and hypotenuse = adjacent side and if A = 90° then the hypotenuse = opposite side. So by using the above formulas for the trigonometric ratios and if the length of the hypotenuse is a.
if A = 0°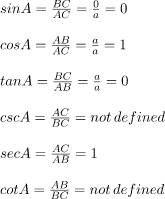
if A = 90°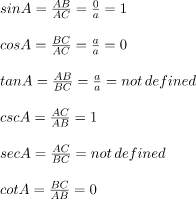
Here csc 0, cot 0, tan 90 and sec 90 are not defined as at the particular angle it is divided by 0 which is undefined.
B. For angles 30° and 60°
Consider an equilateral triangle ABC. Since each angle in an equilateral triangle is 60°, therefore, ∠A = ∠B = ∠C = 60°.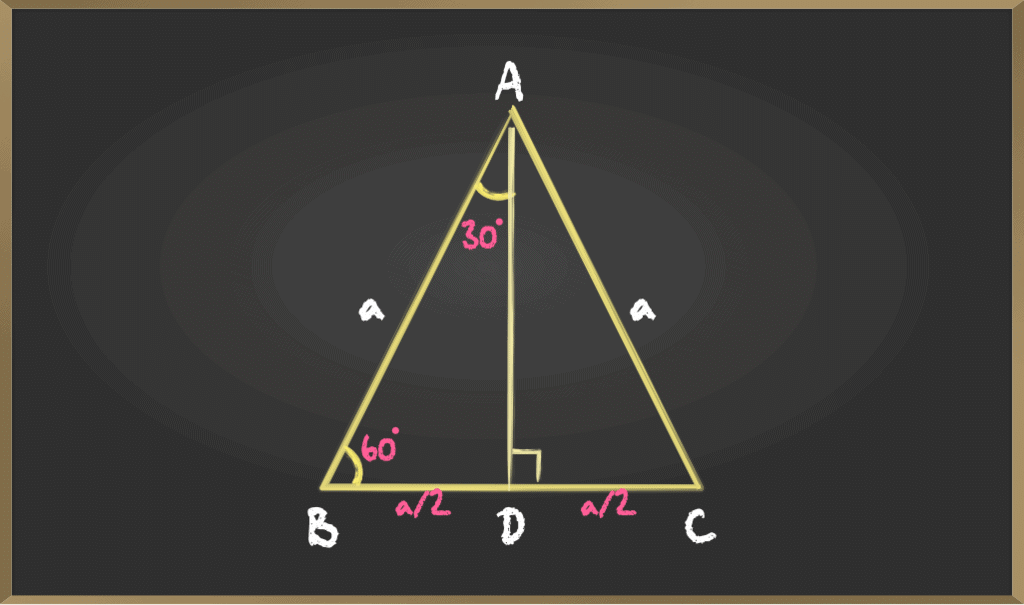 ∆ABD is a right triangle, right-angled at D with ∠BAD = 30° and ∠ABD = 60°, Here ∆ADB and ∆ADC are similar as they are Corresponding parts of Congruent triangles(CPCT).
∆ABD is a right triangle, right-angled at D with ∠BAD = 30° and ∠ABD = 60°, Here ∆ADB and ∆ADC are similar as they are Corresponding parts of Congruent triangles(CPCT).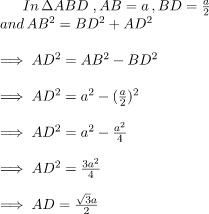
Now we know the values of AB, BD, and AD, So the trigonometric ratios for angle 30 are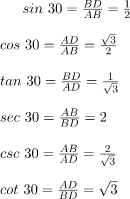
For angle 60°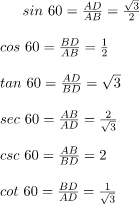
C. For angle 45°
In a right-angled triangle if one angle is 45° then the other angle is also 45° thus making it an isosceles right angle triangle If the length of side BC = a then length of AB = a and Length of AC(hypotenuse) is a√2, then
If the length of side BC = a then length of AB = a and Length of AC(hypotenuse) is a√2, then 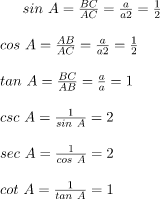
Result
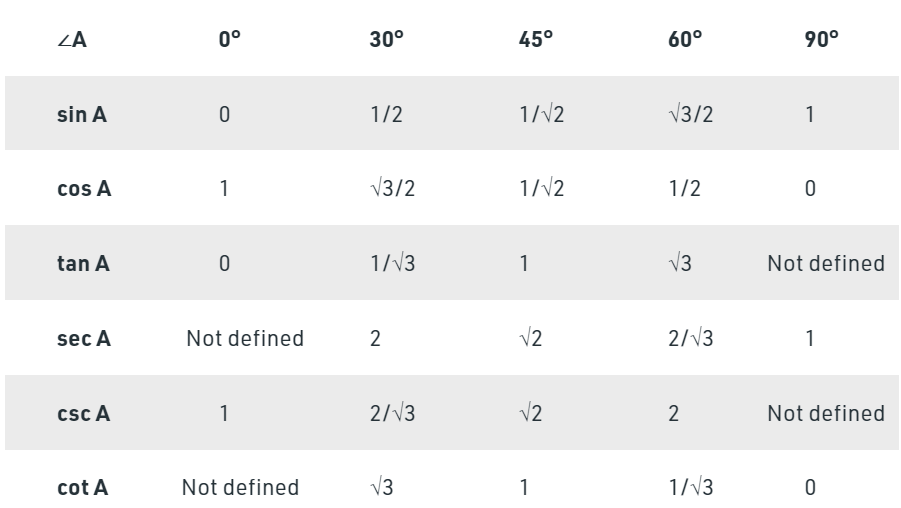
|
85 videos|374 docs|98 tests
|
FAQs on Trigonometric Ratios of Some Specific Angles - Mathematics for SSS 1
| 1. What are the trigonometric ratios of the angles 0°, 30°, 45°, 60°, and 90°? |  |
| 2. How can trigonometric ratios be used to solve problems involving angles in a triangle? |  |
| 3. What is the relationship between trigonometric ratios and the unit circle? |  |
| 4. How can I use the trigonometric ratios to find missing side lengths in right-angled triangles? |  |
| 5. Can trigonometric ratios be used for angles greater than 90°? |  |





















