Trigonometric Identities | Mathematics for Grade 9 PDF Download
Trigonometry is that branch of Mathematics, which relates to the study of angles, measurement of angles, and units of measurement. It also concerns itself with the six ratios for a given angle and the relations satisfied by these ratios. In an extended way, the study is also of the angles forming the elements of a triangle. Logically, a discussion of the properties of a triangle; solving a triangle, physical problems in the area of heights and distances using the properties of a triangle – all constitute a part of the study. It also provides a method of solution of trigonometric equations.
Trigonometric Identity
An equation involving trigonometric ratios of an angle is called trigonometric Identity if it is true for all values of the angle. These are useful whenever trigonometric functions are involved in an expression or an equation. The six basic trigonometric ratios are sine, cosine, tangent, cosecant, secant, and cotangent. All these trigonometric ratios are defined using the sides of the right triangle, such as an adjacent side, opposite side, and hypotenuse side.
Proof of the Trigonometric Identities
For any acute angle θ, prove that
(i) tanθ = sinθ/cosθ
(ii) cotθ = cosθ/sinθ
(iii) tanθ . cotθ = 1
(iv) sin2θ + cos2θ = 1
(v) 1 + tan2θ = sec2θ
(vi) 1 + cot2θ = cosec2θ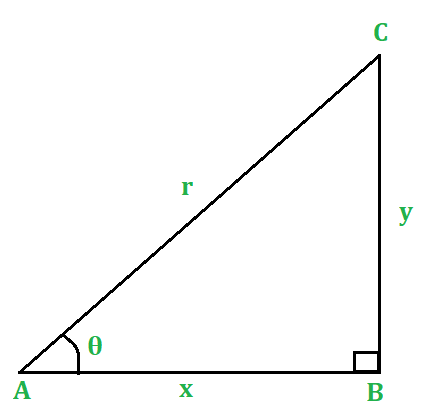
Proof:
Consider a right-angled △ABC (fig. 1) in which ∠B = 90° and ∠A = 0°.
Let AB = x units, BC y units and AC = r units.
Then,
(i) tanθ = y/x = (y/r)/(x/r) [dividing num. and denom. by r]
∴ tanθ = sinθ/cosθ
(ii) cotθ = x/y = (x/r)/(y/r) [dividing num. and denom. by r]
∴ cotθ = cosθ/sinθ
(iii) tanθ . cotθ = (sinθ/cosθ) . (cosθ/sinθ)
tanθ . cotθ = 1
Then, by Pythagoras’ theorem, we have
x2 + y2 = r2.
Now,
(iv) sin2θ + cos2θ = (y/r)2 + (x/r)2 = ( y2/r2 + x2/r2)
= (x2 + y2)/r2 = r2/r2 = 1 [x2+ y2 = r2]
sin2θ + cos2θ = 1
(v) 1 + tan2θ = 1 + (y/x)2 = 1 + y2/x2 = (y2 + x2)/x2 = r2/x2 [x2 + y2 = r2]
(r/x)2 = sec2θ
∴ 1 + tan2θ = sec2θ.
(vi) 1 + cot2θ = 1 + (x/y)2 = 1 + x2/y2 = (x2 + y2)/y2 = r2/y2 [x2 + y2 = r2]
(r2/y2) = cosec2θ
∴ 1 + cot2θ = cosec2θ.
Application of Trigonometric Identites
Application 1: Prove that (1 – sin2θ) sec2θ = 1
Proof:
We have:
LHS = (1 – sin2θ) sec2θ
= cos2θ . sec2θ
= cos2θ . (1/cos2θ)
=1
= RHS.
∴ LHS = RHS.
Application 2: Prove that (1 + tan2θ) cos2θ = 1
Proof:
We have:
LHS = (1 + tan2θ)cos2θ
= sec2θ . cos2θ
= (1/cos2θ) . cos2θ
= 1 = RHS.
∴ LHS=RHS.
Application 3: Prove that (cosec2θ – 1) tan²θ = 1
Proof:
We have:
LHS = (cosec²θ – 1) tan2θ
= (1 + cot2θ – 1) tan2θ
= cot2θ . tan2θ
= (1/tan2θ) . tan2θ
= 1 = RHS.
∴ LHS=RHS.
Application 4: Prove that (sec4θ – sec2θ) = (tan2θ + tan4θ)
Proof:
We have:
LHS = (sec4θ – sec2θ)
= sec2θ(sec2θ – 1)
= (1 + tan2θ) (1 + tan2θ – 1)
= (1 + tan2θ) tan2θ
= (tan2θ + tan4θ)
= RHS
∴ LHS = RHS.
Application 5: Prove that √(sec2θ + cosec2θ) = (tanθ + cotθ)
Proof:
We have:
LHS = √(sec2θ + cosec2θ ) = √((1 + tan2θ) + (1 + cot2θ))
= √(tan2θ + cot2θ + 2)
= √(tan2θ + cot2θ + 2tanθ.cotθ ) (tanθ . cotθ = 1)
= √(tanθ + cotθ)2
= tanθ + cotθ = RHS
∴ LHS = RHS.
|
67 videos|315 docs|92 tests
|
FAQs on Trigonometric Identities - Mathematics for Grade 9
| 1. What are trigonometric identities? |  |
| 2. What is the importance of trigonometric identities? |  |
| 3. How do I prove trigonometric identities? |  |
| 4. What are some commonly used trigonometric identities? |  |
| 5. How can I apply trigonometric identities in real-life situations? |  |

|
Explore Courses for Grade 9 exam
|

|

















