Subset Sum Problem | Algorithms - Computer Science Engineering (CSE) PDF Download
Introduction
Given a set of non-negative integers, and a value sum, determine if there is a subset of the given set with sum equal to given sum.
Example:
- Input: set[] = {3, 34, 4, 12, 5, 2}, sum = 9
Output: True
There is a subset (4, 5) with sum 9. - Input: set[] = {3, 34, 4, 12, 5, 2}, sum = 30
Output: False
There is no subset that add up to 30.
Methods
1. Method 1: Recursion.
Approach: For the recursive approach we will consider two cases.
- Consider the last element and now the required sum = target sum – value of ‘last’ element and number of elements = total elements – 1
- Leave the ‘last’ element and now the required sum = target sum and number of elements = total elements – 1
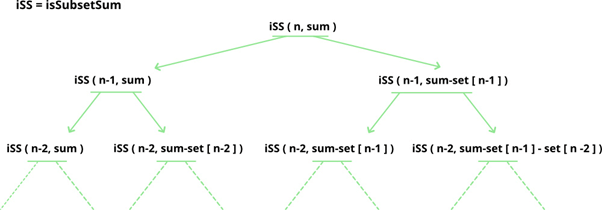
Following is the recursive formula for isSubsetSum() problem:
isSubsetSum(set, n, sum)
= isSubsetSum(set, n-1, sum) ||
isSubsetSum(set, n-1, sum-set[n-1])
Base Cases:
isSubsetSum(set, n, sum) = false, if sum > 0 and n == 0
isSubsetSum(set, n, sum) = true, if sum == 0
Let’s take a look at the simulation of above approach:
set[] = {3, 4, 5, 2}
sum = 9
(x, y) = 'x' is the left number of elements,
'y' is the required sum
- C++

- Java

- Python3

- C#

- PHP

- Javascript

Output: Found a subset with given sum
Complexity Analysis: The above solution may try all subsets of given set in worst case. Therefore time complexity of the above solution is exponential. The problem is in-fact NP-Complete (There is no known polynomial time solution for this problem).
2. Method 2: To solve the problem in Pseudo-polynomial time use the Dynamic programming.
So we will create a 2D array of size (arr.size() + 1) * (target + 1) of type boolean. The state DP[i][j] will be true if there exists a subset of elements from A[0….i] with sum value = ‘j’.
The approach for the problem is:
if (A[i-1] > j)
DP[i][j] = DP[i-1][j]
else
DP[i][j] = DP[i-1][j] OR DP[i-1][j-A[i-1]]
- This means that if current element has value greater than ‘current sum value’ we will copy the answer for previous cases
- And if the current sum value is greater than the ‘ith’ element we will see if any of previous states have already experienced the sum=’j’ OR any previous states experienced a value ‘j – A[i]’ which will solve our purpose.
The below simulation will clarify the above approach:
Below is the implementation of the above approach:
- C++


- Java


- Python3


- C#


- PHP


- Javascript


Output: Found a subset with given sum
Memoization Technique for finding Subset Sum
Method:
- In this method, we also follow the recursive approach but In this method, we use another 2-D matrix in we first initialize with -1 or any negative value.
- In this method, we avoid the few of the recursive call which is repeated itself that’s why we use 2-D matrix. In this matrix we store the value of the previous call value.
Below is the implementation of the above approach:
- C++


Output: YES
Complexity Analysis
- Time Complexity: O(sum * n), where sum is the ‘target sum’ and ‘n’ is the size of array.
- Auxiliary Space: O(sum * n), as the size of 2-D array is sum * n.
|
81 videos|80 docs|33 tests
|

|
Explore Courses for Computer Science Engineering (CSE) exam
|

|





































