Min Cost Path | Algorithms - Computer Science Engineering (CSE) PDF Download
Min Cost Path
Given a cost matrix cost[][] and a position (m, n) in cost[][], write a function that returns cost of minimum cost path to reach (m, n) from (0, 0). Each cell of the matrix represents a cost to traverse through that cell. The total cost of a path to reach (m, n) is the sum of all the costs on that path (including both source and destination). You can only traverse down, right and diagonally lower cells from a given cell, i.e., from a given cell (i, j), cells (i+1, j), (i, j+1), and (i+1, j+1) can be traversed. You may assume that all costs are positive integers.
For example, in the following figure, what is the minimum cost path to (2, 2)? 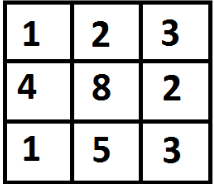 The path with minimum cost is highlighted in the following figure. The path is (0, 0) –> (0, 1) –> (1, 2) –> (2, 2). The cost of the path is 8 (1 + 2 + 2 + 3).
The path with minimum cost is highlighted in the following figure. The path is (0, 0) –> (0, 1) –> (1, 2) –> (2, 2). The cost of the path is 8 (1 + 2 + 2 + 3). 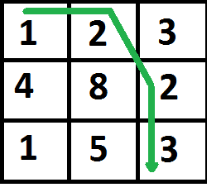
1. Optimal Substructure
The path to reach (m, n) must be through one of the 3 cells: (m-1, n-1) or (m-1, n) or (m, n-1). So minimum cost to reach (m, n) can be written as “minimum of the 3 cells plus cost[m][n]”. minCost(m, n) = min (minCost(m-1, n-1), minCost(m-1, n), minCost(m, n-1)) + cost[m][n]
2. Overlapping Subproblems
Following is a simple recursive implementation of the MCP (Minimum Cost Path) problem.
The implementation simply follows the recursive structure mentioned above:
- C++


C

- Java

- Python3

- C#


- PHP

- Javascript

Output: 8
It should be noted that the above function computes the same subproblems again and again. See the following recursion tree, there are many nodes which appear more than once. The time complexity of this naive recursive solution is exponential and it is terribly slow.
mC refers to minCost()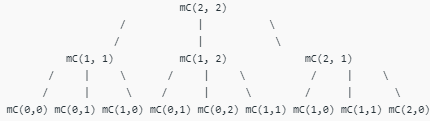
So the MCP problem has both properties (see this and this) of a dynamic programming problem. Like other typical Dynamic Programming(DP) problems, recomputations of the same subproblems can be avoided by constructing a temporary array tc[][] in a bottom-up manner.
- C++


- C


- Java


- Python

- C#


- PHP


- Javascript


Output: 8
Time Complexity of the DP implementation is O(mn) which is much better than Naive Recursive implementation.
Space Optimization
The idea is to use the same given array to store the solutions of subproblems.
- C++

- Java


- Python3

- C#


- Javascript


Output: 8
Alternate Solution
We can also use the Dijkstra’s shortest path algorithm. Below is the implementation of the approach:
- C++




Output: 7
Using a reverse priority queue in this solution can reduce the time complexity compared with a full scan looking for the node with minimum path cost. The overall Time Complexity of the DP implementation is O(mn) without consideration of priority queue in use, which is much better than Naive Recursive implementation.
|
81 videos|113 docs|33 tests
|
















