Computer Science Engineering (CSE) Exam > Computer Science Engineering (CSE) Notes > Algorithms > Asymptotic Notations
Asymptotic Notations | Algorithms - Computer Science Engineering (CSE) PDF Download
Introduction
Asymptotic notations are mathematical tools to represent the time complexity of algorithms for asymptotic analysis.
The following 3 asymptotic notations are mostly used to represent the time complexity of algorithms: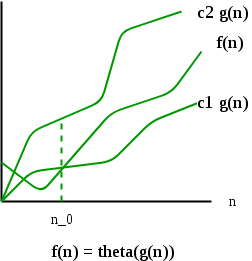
- Θ Notation: The theta notation bounds a function from above and below, so it defines exact asymptotic behavior.
A simple way to get Theta notation of an expression is to drop low order terms and ignore leading constants. For example, consider the following expression.
3n3 + 6n2 + 6000 = Θ(n3)
Dropping lower order terms is always fine because there will always be a number(n) after which Θ(n3) has higher values than Θ(n2) irrespective of the constants involved.
For a given function g(n), we denote Θ(g(n)) is following set of functions.
Θ(g(n)) = {f(n): there exist positive constants c1, c2 and n0 such
that 0 <= c1 * g(n) <= f(n) <= c2 * g(n) for all n >= n0}
The above definition means, if f(n) is theta of g(n), then the value f(n) is always between c1*g(n) and c2*g(n) for large values of n (n >= n0). The definition of theta also requires that f(n) must be non-negative for values of n greater than n0.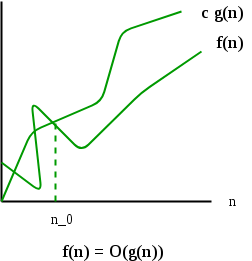
- Big O Notation: The Big O notation defines an upper bound of an algorithm, it bounds a function only from above. For example, consider the case of Insertion Sort. It takes linear time in best case and quadratic time in worst case. We can safely say that the time complexity of Insertion sort is O(n^2). Note that O(n^2) also covers linear time.
If we use Θ notation to represent time complexity of Insertion sort, we have to use two statements for best and worst cases:
(i) The worst case time complexity of Insertion Sort is Θ(n^2).
(ii) The best case time complexity of Insertion Sort is Θ(n).
The Big O notation is useful when we only have upper bound on time complexity of an algorithm. Many times we easily find an upper bound by simply looking at the algorithm.
O(g(n)) = { f(n): there exist positive constants c and
n0 such that 0 <= f(n) <= c*g(n) for
all n >= n0}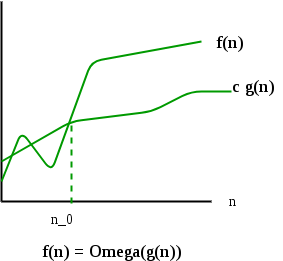
- Ω Notation: Just as Big O notation provides an asymptotic upper bound on a function, Ω notation provides an asymptotic lower bound.
Ω Notation can be useful when we have lower bound on time complexity of an algorithm. As discussed in the previous post, the best case performance of an algorithm is generally not useful, the Omega notation is the least used notation among all three.
For a given function g(n), we denote by Ω(g(n)) the set of functions.
Ω (g(n)) = {f(n): there exist positive constants c and
n0 such that 0 <= c*g(n) <= f(n) for
all n >= n0}.
Let us consider the same Insertion sort example here. The time complexity of Insertion Sort can be written as Ω(n), but it is not a very useful information about insertion sort, as we are generally interested in worst case and sometimes in average case.
Properties of Asymptotic Notations
As we have gone through the definition of this three notations let’s now discuss some important properties of those notations.
- General Properties
If f(n) is O(g(n)) then a * f(n) is also O(g(n)) ; where a is a constant.
Example: f(n) = 2n² + 5 is O(n²)
then 7 * f(n) = 7(2n² + 5) = 14n² + 35 is also O(n²) .
Similarly this property satisfies for both Θ and Ω notation.
We can say
If f(n) is Θ(g(n)) then a * f(n) is also Θ(g(n)) ; where a is a constant.
If f(n) is Ω (g(n)) then a * f(n) is also Ω (g(n)) ; where a is a constant. - Transitive Properties
If f(n) is O(g(n)) and g(n) is O(h(n)) then f(n) = O(h(n)) .
Example: if f(n) = n, g(n) = n² and h(n) = n³
n is O(n²) and n² is O(n³)
then n is O(n³)
Similarly, this property satisfies for both Θ and Ω notation.
We can say
If f(n) is Θ(g(n)) and g(n) is Θ(h(n)) then f(n) = Θ(h(n)) .
If f(n) is Ω (g(n)) and g(n) is Ω (h(n)) then f(n) = Ω (h(n)) - Reflexive Properties
Reflexive properties are always easy to understand after transitive.
If f(n) is given then f(n) is O(f(n)). Since MAXIMUM VALUE OF f(n) will be f(n) ITSELF !
Hence x = f(n) and y = O(f(n) tie themselves in reflexive relation always.
Example: f(n) = n² ; O(n²) i.e O(f(n))
Similarly, this property satisfies for both Θ and Ω notation.
We can say that:
If f(n) is given then f(n) is Θ(f(n)).
If f(n) is given then f(n) is Ω (f(n)). - Symmetric Properties
If f(n) is Θ(g(n)) then g(n) is Θ(f(n)).
Example: f(n) = n² and g(n) = n²
then f(n) = Θ(n²) and g(n) = Θ(n²)
This property only satisfies for Θ notation. - Transpose Symmetric Properties
If f(n) is O(g(n)) then g(n) is Ω (f(n)).
Example: f(n) = n , g(n) = n²
then n is O(n²) and n² is Ω (n)
This property only satisfies for O and Ω notations. - Some More Properties
(i) If f(n) = O(g(n)) and f(n) = Ω(g(n)) then f(n) = Θ(g(n))
(ii) If f(n) = O(g(n)) and d(n) = O(e(n))
then f(n) + d(n) = O( max( g(n), e(n) ))
Example: f(n) = n i.e O(n)
d(n) = n² i.e O(n²)
then f(n) + d(n) = n + n² i.e O(n²)
(iii) If f(n) = O(g(n)) and d(n) = O(e(n))
then f(n) * d(n) = O( g(n) * e(n) )
Example: f(n) = n i.e O(n)
d(n) = n² i.e O(n²)
then f(n) * d(n) = n * n² = n³ i.e O(n³)
Little O and Little Omega Notations
The main idea of asymptotic analysis is to have a measure of efficiency of algorithms that doesn’t depend on machine specific constants, mainly because this analysis doesn’t require algorithms to be implemented and time taken by programs to be compared. We have already discussed Three main asymptotic notations.
The following 2 more asymptotic notations are used to represent time complexity of algorithms:
- Little ο asymptotic notation
Big-Ο is used as a tight upper-bound on the growth of an algorithm’s effort (this effort is described by the function f(n)), even though, as written, it can also be a loose upper-bound. “Little-ο” (ο()) notation is used to describe an upper-bound that cannot be tight.
Definition: Let f(n) and g(n) be functions that map positive integers to positive real numbers. We say that f(n) is ο(g(n)) (or f(n) Ε ο(g(n))) if for any real constant c > 0, there exists an integer constant n0 ≥ 1 such that 0 ≤ f(n) < c*g(n).
Thus, little o() means loose upper-bound of f(n). Little o is a rough estimate of the maximum order of growth whereas Big-Ο may be the actual order of growth.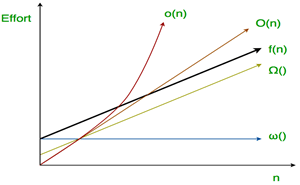 In mathematical relation, f(n) = o(g(n)) means lim f(n) / g(n) = 0
In mathematical relation, f(n) = o(g(n)) means lim f(n) / g(n) = 0
n → ∞
Examples:
Is 7n + 8 ∈ o(n2)?
In order for that to be true, for any c, we have to be able to find an n0 that makes
f(n) < c * g(n) asymptotically true.
lets took some example,
If c = 100,we check the inequality is clearly true. If c = 1 / 100 , we’ll have to use
a little more imagination, but we’ll be able to find an n0. (Try n0 = 1000.) From
these examples, the conjecture appears to be correct.
then check limits,
lim f(n)/g(n) = lim (7n + 8) / (n2) = lim 7 / 2n = 0 (l’hospital)
n → ∞ n → ∞ n → ∞
Hence 7n + 8 ∈ o(n2) - Little ω asymptotic notation
Definition : Let f(n) and g(n) be functions that map positive integers to positive real numbers. We say that f(n) is ω(g(n)) (or f(n) ∈ ω(g(n))) if for any real constant c > 0, there exists an integer constant n0 ≥ 1 such that f(n) > c * g(n) ≥ 0 for every integer n ≥ n0.
f(n) has a higher growth rate than g(n) so main difference between Big Omega (Ω) and little omega (ω) lies in their definitions.In the case of Big Omega f(n) = Ω(g(n)) and the bound is 0 <= cg(n) <= f(n), but in case of little omega, it is true for 0 <= c * g(n) < f(n).
The relationship between Big Omega (Ω) and Little Omega (ω) is similar to that of Big-Ο and Little o except that now we are looking at the lower bounds. Little Omega (ω) is a rough estimate of the order of the growth whereas Big Omega (Ω) may represent exact order of growth. We use ω notation to denote a lower bound that is not asymptotically tight.
And, f(n) ∈ ω(g(n)) if and only if g(n) ∈ ο((f(n)).
In mathematical relation,
if f(n) ∈ ω(g(n)) then,
lim f(n)/g(n) = ∞
n→∞
Example:
Prove that 4n + 6 ∈ ω(1);
the little omega(ο) running time can be proven by applying limit formula given below.
if lim f(n) / g(n) = ∞ then functions f(n) is ω(g(n))
n→∞
here,we have functions f(n) = 4n + 6 and g(n) = 1
lim (4n + 6) / (1) = ∞
n→∞
and,also for any c we can get n0 for this inequality 0 <= c*g(n) < f(n), 0 <= c * 1 < 4n + 6
Hence proved.
The document Asymptotic Notations | Algorithms - Computer Science Engineering (CSE) is a part of the Computer Science Engineering (CSE) Course Algorithms.
All you need of Computer Science Engineering (CSE) at this link: Computer Science Engineering (CSE)
|
81 videos|113 docs|33 tests
|
FAQs on Asymptotic Notations - Algorithms - Computer Science Engineering (CSE)
| 1. What are asymptotic notations in computer science engineering? |  |
Ans. Asymptotic notations in computer science engineering are mathematical tools used to describe the performance of an algorithm in terms of its input size. They provide a way to analyze the efficiency and scalability of algorithms by focusing on how the algorithm's runtime or space requirements grow as the input size increases.
| 2. What are the commonly used asymptotic notations in computer science engineering? |  |
Ans. The commonly used asymptotic notations in computer science engineering are:
- Big O notation (O): It represents the upper bound of an algorithm's time or space complexity.
- Omega notation (Ω): It represents the lower bound of an algorithm's time or space complexity.
- Theta notation (Θ): It represents both the upper and lower bounds of an algorithm's time or space complexity.
These notations are used to categorize algorithms based on their growth rates and provide a standardized way to compare their efficiency.
| 3. How is Big O notation (O) used in computer science engineering? |  |
Ans. Big O notation (O) is used in computer science engineering to analyze the worst-case scenario of an algorithm's time or space complexity. It represents the upper bound of the algorithm's performance. For example, if an algorithm has a time complexity of O(n^2), it means that the algorithm's runtime will not exceed a quadratic function of the input size (n). Big O notation provides a way to compare the efficiency of different algorithms and helps in selecting the most suitable algorithm for a given problem.
| 4. What is the significance of asymptotic notations in computer science engineering? |  |
Ans. Asymptotic notations are significant in computer science engineering for the following reasons:
- They provide a standardized way to express and compare the efficiency of algorithms.
- They help in selecting the most suitable algorithm for a given problem by considering its time or space complexity.
- They allow engineers to analyze and predict the performance of algorithms as the input size grows, aiding in designing scalable systems.
- They assist in understanding the trade-offs between time and space complexity and making informed decisions in algorithm design.
- They are widely used in algorithm analysis, data structure design, and optimization techniques, making them essential in computer science engineering.
| 5. How can asymptotic notations be used to analyze the efficiency of algorithms? |  |
Ans. Asymptotic notations can be used to analyze the efficiency of algorithms by providing a framework to measure their time or space complexity. By using notations like Big O, Omega, and Theta, engineers can estimate how an algorithm's performance scales with the input size. This analysis helps in identifying the growth rate of an algorithm and understanding its efficiency relative to other algorithms. By analyzing the efficiency, engineers can optimize algorithms, choose the best algorithm for a given problem, and design systems that can handle large-scale inputs efficiently.
Related Searches
















