Longest Common Subsequence | Algorithms - Computer Science Engineering (CSE) PDF Download
Longest Common Subsequence
Let us discuss Longest Common Subsequence (LCS) problem as one more example problem that can be solved using Dynamic Programming.
LCS Problem Statement: Given two sequences, find the length of longest subsequence present in both of them. A subsequence is a sequence that appears in the same relative order, but not necessarily contiguous. For example, “abc”, “abg”, “bdf”, “aeg”, ‘”acefg”, .. etc are subsequences of “abcdefg”.
In order to find out the complexity of brute force approach, we need to first know the number of possible different subsequences of a string with length n, i.e., find the number of subsequences with lengths ranging from 1,2,..n - 1. Recall from theory of permutation and combination that number of combinations with 1 element are nC1. Number of combinations with 2 elements are nC2 and so forth and so on. We know that nC0 + nC1 + nC2 + … nCn = 2n. So a string of length n has 2n-1 different possible subsequences since we do not consider the subsequence with length 0. This implies that the time complexity of the brute force approach will be O(n * 2n). Note that it takes O(n) time to check if a subsequence is common to both the strings. This time complexity can be improved using dynamic programming.
It is a classic computer science problem, the basis of diff (a file comparison program that outputs the differences between two files), and has applications in bioinformatics.
Examples:
- LCS for input Sequences “ABCDGH” and “AEDFHR” is “ADH” of length 3.
- LCS for input Sequences “AGGTAB” and “GXTXAYB” is “GTAB” of length 4.
The naive solution for this problem is to generate all subsequences of both given sequences and find the longest matching subsequence. This solution is exponential in term of time complexity. Let us see how this problem possesses both important properties of a Dynamic Programming (DP) Problem.
- Optimal Substructure:
Let the input sequences be X[0..m-1] and Y[0..n-1] of lengths m and n respectively. And let L(X[0..m-1], Y[0..n-1]) be the length of LCS of the two sequences X and Y. Following is the recursive definition of L(X[0..m-1], Y[0..n-1]).
If last characters of both sequences match (or X[m-1] == Y[n-1]) then L(X[0..m-1], Y[0..n-1]) = 1 + L(X[0..m-2], Y[0..n-2])
If last characters of both sequences do not match (or X[m-1] != Y[n-1]) then L(X[0..m-1], Y[0..n-1]) = MAX ( L(X[0..m-2], Y[0..n-1]), L(X[0..m-1], Y[0..n-2]) )
Examples:
(i) Consider the input strings “AGGTAB” and “GXTXAYB”. Last characters match for the strings. So length of LCS can be written as:
L(“AGGTAB”, “GXTXAYB”) = 1 + L(“AGGTA”, “GXTXAY”) (ii) Consider the input strings “ABCDGH” and “AEDFHR. Last characters do not match for the strings. So length of LCS can be written as:
(ii) Consider the input strings “ABCDGH” and “AEDFHR. Last characters do not match for the strings. So length of LCS can be written as:
L(“ABCDGH”, “AEDFHR”) = MAX ( L(“ABCDG”, “AEDFHR”), L(“ABCDGH”, “AEDFH”) )
So the LCS problem has optimal substructure property as the main problem can be solved using solutions to subproblems. - Overlapping Subproblems:
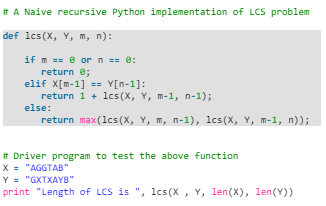
Following is simple recursive implementation of the LCS problem. The implementation simply follows the recursive structure mentioned above.
- C++

- C

- Java

- Python

- C#

- PHP

Output: Length of LCS is 4
Time complexity of the above naive recursive approach is O(2^n) in worst case and worst case happens when all characters of X and Y mismatch i.e., length of LCS is 0.
Considering the above implementation, following is a partial recursion tree for input strings “AXYT” and “AYZX”
In the above partial recursion tree, lcs(“AXY”, “AYZ”) is being solved twice. If we draw the complete recursion tree, then we can see that there are many subproblems which are solved again and again. So this problem has Overlapping Substructure property and recomputation of same subproblems can be avoided by either using Memoization or Tabulation. Following is a tabulated implementation for the LCS problem.
- C++


- C


- Java


- Python

- C#


- PHP


Output: Length of LCS is 4
Time Complexity of the above implementation is O(mn) which is much better than the worst-case time complexity of Naive Recursive implementation.
|
81 videos|80 docs|33 tests
|
FAQs on Longest Common Subsequence - Algorithms - Computer Science Engineering (CSE)
| 1. What is a Longest Common Subsequence (LCS)? |  |
| 2. How is the length of the Longest Common Subsequence computed? |  |
| 3. What is the time complexity of finding the Longest Common Subsequence? |  |
| 4. Can the Longest Common Subsequence have multiple solutions? |  |
| 5. Can the Longest Common Subsequence be empty? |  |

|
Explore Courses for Computer Science Engineering (CSE) exam
|

|
 (ii) Consider the input strings “ABCDGH” and “AEDFHR. Last characters do not match for the strings. So length of LCS can be written as:
(ii) Consider the input strings “ABCDGH” and “AEDFHR. Last characters do not match for the strings. So length of LCS can be written as: