Undirected Graph | Algorithms - Computer Science Engineering (CSE) PDF Download

Detect Cycle in an Undirected Graph

A disjoint-set data structure is a data structure that keeps track of a set of elements partitioned into a number of disjoint (non-overlapping) subsets. A union-find algorithm is an algorithm that performs two useful operations on such a data structure:

Find: Determine which subset a particular element is in. This can be used for determining if two elements are in the same subset.

Union: Join two subsets into a single subset.
In this, we will discuss the application of Disjoint Set Data Structure. The application is to check whether a given graph contains a cycle or not.

Union: Find Algorithm can be used to check whether an undirected graph contains cycle or not. Note that we have discussed an algorithm to detect cycle. This is another method based on Union-Find. This method assumes that the graph doesn’t contain any self-loops. 

We can keep track of the subsets in a 1D array, let’s call it parent[].

Let us consider the following graph: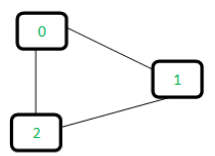

For each edge, make subsets using both the vertices of the edge. If both the vertices are in the same subset, a cycle is found.
Initially, all slots of parent array are initialized to -1 (means there is only one item in every subset).
0   1   2
-1 -1  -1

Now process all edges one by one:

1. Edge 0-1: Find the subsets in which vertices 0 and 1 are. Since they are in different subsets, we take the union of them. For taking the union, either make node 0 as parent of node 1 or vice-versa.
   0   1   2    <----- 1 is made parent of 0 (1 is now representative of subset {0, 1})
   1  -1  -1
2. Edge 1-2: 1 is in subset 1 and 2 is in subset 2. So, take union.
   0   1   2    <----- 2 is made parent of 1 (2 is now representative of subset {0, 1, 2})
   1   2  -1
3. Edge 0-2: 0 is in subset 2 and 2 is also in subset 2. Hence, including this edge forms a cycle.
   How subset of 0 is same as 2?
   0->1->2 // 1 is parent of 0 and 2 is parent of 1  

Based on the above explanation, below are implementations:

• C++
   
  
  
• C
  
  
  
• Java
  
  
  
• Python
  
  
• C#
  
  
  

Output: graph contains cycle

Detect cycle in an undirected graph

Given an undirected graph, how to check if there is a cycle in the graph?
Example:
1. Input: n = 4, e = 4
Output: Yes
Explanation:
0 1, 1 2, 2 3, 0 2
Diagram: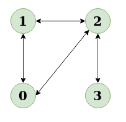
The diagram clearly shows a cycle 0 to 2 to 1 to 0

2. Input: n = 4, e = 3
0 1, 1 2, 2 3
Output: No
Explanation:
Diagram: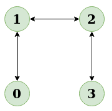
The diagram clearly shows no cycle 

Articles about cycle detection:

• cycle detection for directed graph.
• union-find algorithm for cycle detection in undirected graphs.

Approach: Run a DFS from every unvisited node. Depth First Traversal can be used to detect a cycle in a Graph. DFS for a connected graph produces a tree. There is a cycle in a graph only if there is a back edge present in the graph. A back edge is an edge that is joining a node to itself (self-loop) or one of its ancestor in the tree produced by DFS.
To find the back edge to any of its ancestor keep a visited array and if there is a back edge to any visited node then there is a loop and return true.

Algorithm: 

1. Create the graph using the given number of edges and vertices.
2. Create a recursive function that that current index or vertex, visited and recursion stack.
3. Mark the current node as visited and also mark the index in recursion stack.
4. Find all the vertices which are not visited and are adjacent to the current node. Recursively call the function for those vertices, If the recursive function returns true return true.
5. If the adjacent vertices are already marked in the recursion stack then return true.
6. Create a wrapper class, that calls the recursive function for all the vertices and if any function returns true, return true.
7. Else if for all vertices the function returns false return false.

Dry Run: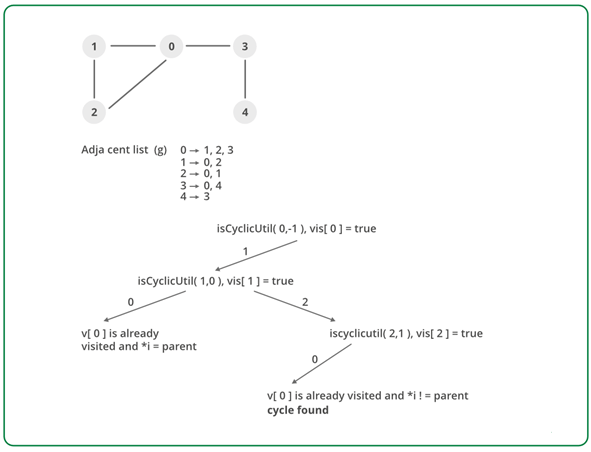
Implementation:

• C++
  
  
  
  
• Java
  
  
  
• Python
  
  
• C#
  
  
  

Output:

• Graph contains cycle
• Graph doesn't contain cycle

Complexity Analysis:

• Time Complexity: O(V+E).
  The program does a simple DFS Traversal of the graph which is represented using adjacency list. So the time complexity is O(V+E).
• Space Complexity: O(V).
  To store the visited array O(V) space is required. 

Biconnected Components

A biconnected component is a maximal biconnected subgraph.
Biconnected Graph is already discussed here. In this, we will see how to find biconnected component in a graph using algorithm by John Hopcroft and Robert Tarjan.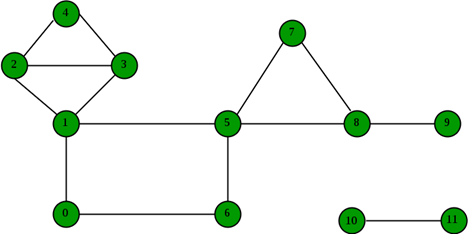

In above graph, following are the biconnected components:

• 4–2 3–4 3–1 2–3 1–2
• 8–9
• 8–5 7–8 5–7
• 6–0 5–6 1–5 0–1
• 10–11

Algorithm is based on Disc and Low Values discussed in Strongly Connected Components Article.

Idea is to store visited edges in a stack while DFS on a graph and keep looking for Articulation Points (highlighted in above figure). As soon as an Articulation Point u is found, all edges visited while DFS from node u onwards will form one biconnected component. When DFS completes for one connected component, all edges present in stack will form a biconnected component.
If there is no Articulation Point in graph, then graph is biconnected and so there will be one biconnected component which is the graph itself.

• C++
  
  
  
  
  // Driver program to test above function
  int main()
  {
  
• Java
  
  
  
  
• Python
  
  
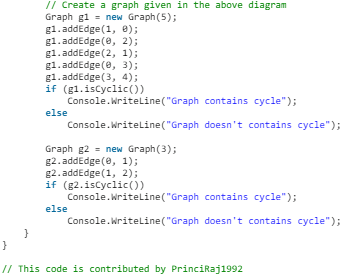
  # Create a graph given in the above diagram
  
• C#
  
  
  
  
  
  }  
  // This code is contributed by PrinciRaj1992

Output:
4--2 3--4 3--1 2--3 1--2
8--9
8--5 7--8 5--7
6--0 5--6 1--5 0--1
10--11
Above are 5 biconnected components in graph