Quick Sort | Algorithms - Computer Science Engineering (CSE) PDF Download

Introduction

Like Merge Sort, QuickSort is a Divide and Conquer algorithm. It picks an element as pivot and partitions the given array around the picked pivot. There are many different versions of quickSort that pick pivot in different ways.

1. Always pick first element as pivot.
2. Always pick last element as pivot (implemented below)
3. Pick a random element as pivot.
4. Pick median as pivot.

The key process in quickSort is partition(). Target of partitions is, given an array and an element x of array as pivot, put x at its correct position in sorted array and put all smaller elements (smaller than x) before x, and put all greater elements (greater than x) after x. All this should be done in linear time.

Pseudo Code for recursive QuickSort function :
/* low  --> Starting index,  high  --> Ending index */
quickSort(arr[], low, high)
{
    if (low < high)
    {
        /* pi is partitioning index, arr[pi] is now
           at right place */
        pi = partition(arr, low, high);
        quickSort(arr, low, pi - 1);  // Before pi
        quickSort(arr, pi + 1, high); // After pi
    }
}

Partition Algorithm

There can be many ways to do partition, following pseudo code adopts the method given in CLRS book. The logic is simple, we start from the leftmost element and keep track of index of smaller (or equal to) elements as i. While traversing, if we find a smaller element, we swap current element with arr[i]. Otherwise we ignore current element.
/* low  --> Starting index,  high  --> Ending index */
quickSort(arr[], low, high)
{
    if (low < high)
    {
        /* pi is partitioning index, arr[pi] is now
           at right place */
        pi = partition(arr, low, high);
        quickSort(arr, low, pi - 1);  // Before pi
        quickSort(arr, pi + 1, high); // After pi
    }
}

Pseudo code for partition()
/* This function takes last element as pivot, places
   the pivot element at its correct position in sorted
    array, and places all smaller (smaller than pivot)
   to left of pivot and all greater elements to right
   of pivot */
partition (arr[], low, high)
{
    // pivot (Element to be placed at right position)
    pivot = arr[high];
    i = (low - 1)  // Index of smaller element and indicates the
                   // right position of pivot found so far
    for (j = low; j <= high- 1; j++)
    {
        // If current element is smaller than the pivot
        if (arr[j] < pivot)
        {
            i++;    // increment index of smaller element
            swap arr[i] and arr[j]
        }
    }
    swap arr[i + 1] and arr[high])
    return (i + 1)
}

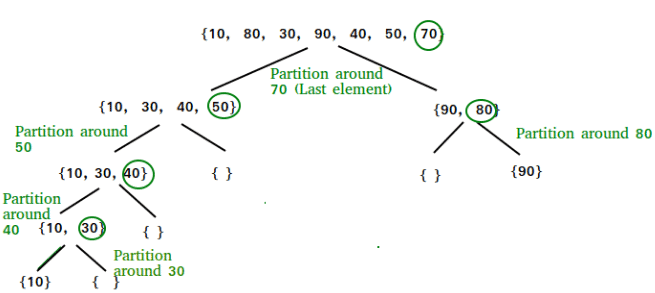
Illustration of partition()
arr[] = {10, 80, 30, 90, 40, 50, 70}
Indexes:  0   1   2   3   4   5   6
low = 0, high =  6, pivot = arr[h] = 70
Initialize index of smaller element, i = -1
Traverse elements from j = low to high-1
j = 0 : Since arr[j] <= pivot, do i++ and swap(arr[i], arr[j])
i = 0
arr[] = {10, 80, 30, 90, 40, 50, 70} // No change as i and j
                                     // are same
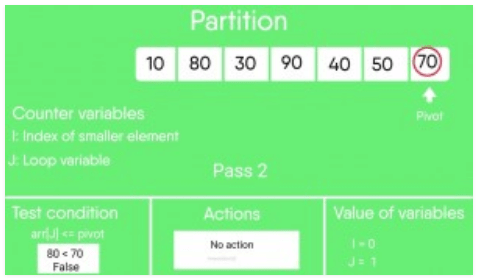
j = 1 : Since arr[j] > pivot, do nothing
// No change in i and arr[]
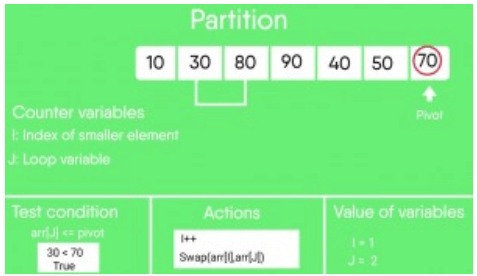
j = 2 : Since arr[j] <= pivot, do i++ and swap(arr[i], arr[j])
i = 1
arr[] = {10, 30, 80, 90, 40, 50, 70} // We swap 80 and 30
j = 3 : Since arr[j] > pivot, do nothing
// No change in i and arr[]

j = 4 : Since arr[j] <= pivot, do i++ and swap(arr[i], arr[j])
i = 2
arr[] = {10, 30, 40, 90, 80, 50, 70} // 80 and 40 Swapped
j = 5 : Since arr[j] <= pivot, do i++ and swap arr[i] with arr[j]
i = 3
arr[] = {10, 30, 40, 50, 80, 90, 70} // 90 and 50 Swapped
We come out of loop because j is now equal to high-1.
Finally we place pivot at correct position by swapping
arr[i+1] and arr[high] (or pivot)
arr[] = {10, 30, 40, 50, 70, 90, 80} // 80 and 70 Swapped
Now 70 is at its correct place. All elements smaller than
70 are before it and all elements greater than 70 are after
it.

Implementation
Following are the implementations of QuickSort:

C++14
 

Java

Python3

Output
Sorted array:
1 5 7 8 9 10

Analysis of QuickSort

Time taken by QuickSort, in general, can be written as following.
T(n) = T(k) + T(n - k - 1) + θ(n)
The first two terms are for two recursive calls, the last term is for the partition process. k is the number of elements which are smaller than pivot.
The time taken by QuickSort depends upon the input array and partition strategy. 

Following are three cases.

1. Worst Case: The worst case occurs when the partition process always picks greatest or smallest element as pivot. If we consider above partition strategy where last element is always picked as pivot, the worst case would occur when the array is already sorted in increasing or decreasing order. Following is recurrence for worst case.
   T(n) = T(θ) + T(n - 1) + θ(n)
   which is equivalent to
   T(n) = T(n - 1) + θ(n)
   The solution of above recurrence is θ(n²).
2. Best Case: The best case occurs when the partition process always picks the middle element as pivot. Following is recurrence for best case.
   T(n) = 2T(n / 2) + θ(n)
   The solution of above recurrence is θ (nLogn). It can be solved using case 2 of Master Theorem.
3. Average Case: To do average case analysis, we need to consider all possible permutation of array and calculate time taken by every permutation which doesn’t look easy.
   We can get an idea of average case by considering the case when partition puts O(n/9) elements in one set and O(9n/10) elements in other set. Following is recurrence for this case.
   T(n) = T(n / 9) + T(9n / 10) + θ(n)
   Solution of above recurrence is also O(nLogn)
   Although the worst case time complexity of QuickSort is O(n2) which is more than many other sorting algorithms like Merge Sort and Heap Sort, QuickSort is faster in practice, because its inner loop can be efficiently implemented on most architectures, and in most real-world data. QuickSort can be implemented in different ways by changing the choice of pivot, so that the worst case rarely occurs for a given type of data. However, merge sort is generally considered better when data is huge and stored in external storage.

Is QuickSort stable?
The default implementation is not stable. However any sorting algorithm can be made stable by considering indexes as comparison parameter.

Is QuickSort In-place?
As per the broad definition of in-place algorithm it qualifies as an in-place sorting algorithm as it uses extra space only for storing recursive function calls but not for manipulating the input.

What is 3-Way QuickSort?
In simple QuickSort algorithm, we select an element as pivot, partition the array around pivot and recur for subarrays on left and right of pivot.
Consider an array which has many redundant elements. For example, {1, 4, 2, 4, 2, 4, 1, 2, 4, 1, 2, 2, 2, 2, 4, 1, 4, 4, 4}. If 4 is picked as pivot in Simple QuickSort, we fix only one 4 and recursively process remaining occurrences. In 3 Way QuickSort, an array arr[l..r] is divided in 3 parts:
(a) arr[l..i] elements less than pivot.
(b) arr[i+1..j-1] elements equal to pivot.
(c) arr[j..r] elements greater than pivot.
See this for implementation.

How to implement QuickSort for Linked Lists?

• QuickSort on Singly Linked List
• QuickSort on Doubly Linked List

Can we implement QuickSort Iteratively? 
Yes, please refer Iterative Quick Sort.

Why Quick Sort is preferred over MergeSort for sorting Arrays
Quick Sort in its general form is an in-place sort (i.e. it doesn’t require any extra storage) whereas merge sort requires O(N) extra storage, N denoting the array size which may be quite expensive. Allocating and de-allocating the extra space used for merge sort increases the running time of the algorithm. Comparing average complexity we find that both type of sorts have O(NlogN) average complexity but the constants differ. For arrays, merge sort loses due to the use of extra O(N) storage space.
Most practical implementations of Quick Sort use randomized version. The randomized version has expected time complexity of O(nLogn). The worst case is possible in randomized version also, but worst case doesn’t occur for a particular pattern (like sorted array) and randomized Quick Sort works well in practice.
Quick Sort is also a cache friendly sorting algorithm as it has good locality of reference when used for arrays.
Quick Sort is also tail recursive, therefore tail call optimizations is done.

Why MergeSort is preferred over QuickSort for Linked Lists?
In case of linked lists the case is different mainly due to difference in memory allocation of arrays and linked lists. Unlike arrays, linked list nodes may not be adjacent in memory. Unlike array, in linked list, we can insert items in the middle in O(1) extra space and O(1) time. Therefore merge operation of merge sort can be implemented without extra space for linked lists.
In arrays, we can do random access as elements are continuous in memory. Let us say we have an integer (4-byte) array A and let the address of A[0] be x then to access A[i], we can directly access the memory at (x + i*4). Unlike arrays, we can not do random access in linked list. Quick Sort requires a lot of this kind of access. In linked list to access i’th index, we have to travel each and every node from the head to i’th node as we don’t have continuous block of memory. Therefore, the overhead increases for quick sort. Merge sort accesses data sequentially and the need of random access is low.

How to optimize QuickSort so that it takes O(Log n) extra space in worst case?
Snapshots: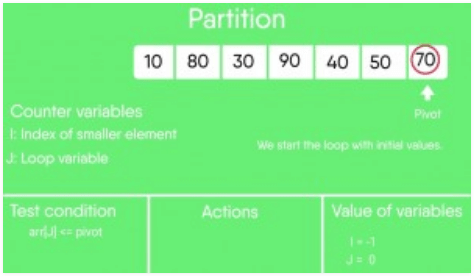

• Quiz on QuickSort
• Recent Articles on QuickSort
• Coding practice for sorting.

Iterative Quick Sort

Following is a typical recursive implementation of Quick Sort that uses last element as pivot.

C++

Java




Output:
2 2 4 6 9

The above implementation can be optimized in many ways:

1. The above implementation uses last index as pivot. This causes worst-case behavior on already sorted arrays, which is a commonly occurring case. The problem can be solved by choosing either a random index for the pivot, or choosing the middle index of the partition or choosing the median of the first, middle and last element of the partition for the pivot. (See this for details)
2. To reduce the recursion depth, recur first for the smaller half of the array, and use a tail call to recurse into the other.
3. Insertion sort works better for small subarrays. Insertion sort can be used for invocations on such small arrays (i.e. where the length is less than a threshold t determined experimentally). For example, this library implementation of qsort uses insertion sort below size 7.
   Despite above optimizations, the function remains recursive and uses function call stack to store intermediate values of l and h. The function call stack stores other bookkeeping information together with parameters. Also, function calls involve overheads like storing activation record of the caller function and then resuming execution.

The above function can be easily converted to iterative version with the help of an auxiliary stack. Following is an iterative implementation of the above recursive code.

C++

C

Java

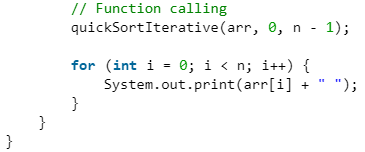
Python

C#

PHP

Output:
1 2 2 3 3 3 4 5
The above mentioned optimizations for recursive quick sort can also be applied to iterative version.

1. Partition process is same in both recursive and iterative. The same techniques to choose optimal pivot can also be applied to iterative version.
2. To reduce the stack size, first push the indexes of smaller half.
3. Use insertion sort when the size reduces below a experimentally calculated threshold.

QuickSort on Singly Linked List

QuickSort on Doubly Linked List is discussed here. QuickSort on Singly linked list was given as an exercise. Following is C++ implementation for same. The important things about implementation are, it changes pointers rather swapping data and time complexity is same as the implementation for Doubly Linked List.
In partition(), we consider last element as pivot. We traverse through the current list and if a node has value greater than pivot, we move it after tail. If the node has smaller value, we keep it at its current position.
In QuickSortRecur(), we first call partition() which places pivot at correct position and returns pivot. After pivot is placed at correct position, we find tail node of left side (list before pivot) and recur for left list. Finally, we recur for right list.

C++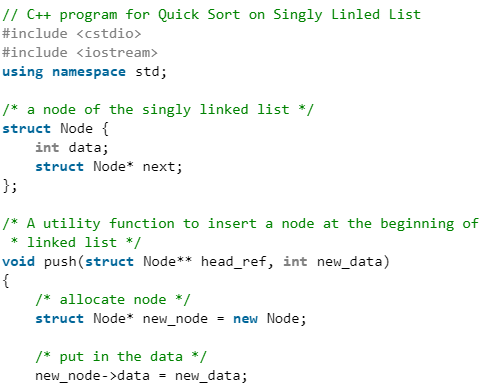

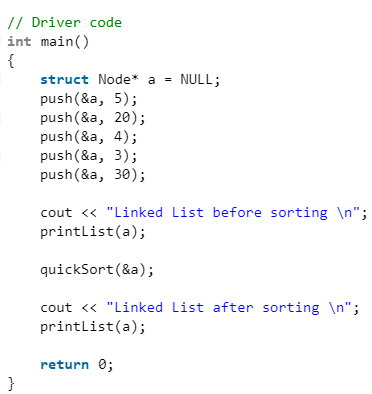
Java

Python3

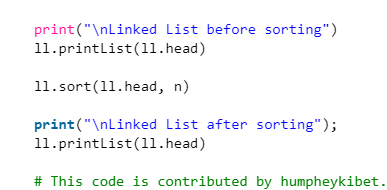
C#

Javascript

Output
Linked List before sorting
30 3 4 20 5
Linked List after sorting
3 4 5 20 30

QuickSort on Doubly Linked List

Following is a typical recursive implementation of QuickSort for arrays. The implementation uses last element as pivot.

C++

Java

Python3

C#

Can we use the same algorithm for Linked List?
Following is C++ implementation for the doubly linked list. The idea is simple, we first find out pointer to the last node. Once we have a pointer to the last node, we can recursively sort the linked list using pointers to first and last nodes of a linked list, similar to the above recursive function where we pass indexes of first and last array elements. The partition function for a linked list is also similar to partition for arrays. Instead of returning index of the pivot element, it returns a pointer to the pivot element. In the following implementation, quickSort() is just a wrapper function, the main recursive function is _quickSort() which is similar to quickSort() for array implementation.
 C++

C

Java

C#

Output:
Linked List before sorting
30  3  4  20  5
Linked List after sorting
3  4  5  20  30
Time Complexity: Time complexity of the above implementation is same as time complexity of QuickSort() for arrays. It takes O(n^2) time in the worst case and O(nLogn) in average and best cases. The worst case occurs when the linked list is already sorted.
Can we implement random quicksort for a linked list?
Quicksort can be implemented for Linked List only when we can pick a fixed point as the pivot (like the last element in the above implementation). Random QuickSort cannot be efficiently implemented for Linked Lists by picking random pivot.