Directed Acyclic Graphs (DAG) | Algorithms - Computer Science Engineering (CSE) PDF Download
| Table of contents |

|
| Detect Cycle in a Directed Graph |

|
| → |

|
| Longest Path in a Directed Acyclic Graph |

|
| Shortest Path in Directed Acyclic Graph |

|
Detect Cycle in a Directed Graph
Given a directed graph, check whether the graph contains a cycle or not. Your function should return true if the given graph contains at least one cycle, else return false.
Example:
1. Input: n = 4, e = 6
0
→
1, 0→
2, 1→
2, 2→
0, 2→
3, 3→
3Output: Yes
Explanation:
Diagram:
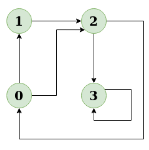 The diagram clearly shows a cycle 0 → 2 → 0
The diagram clearly shows a cycle 0 → 2 → 02. Input: n = 4, e = 4
0 → 1, 0 → 2, 1 → 2, 2 → 3
Output: No
Explanation:
Diagram:
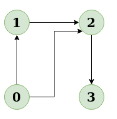
The diagram clearly shows no cycle
Solution using Depth First Search or DFS
- Approach: Depth First Traversal can be used to detect a cycle in a Graph. DFS for a connected graph produces a tree. There is a cycle in a graph only if there is a back edge present in the graph. A back edge is an edge that is from a node to itself (self-loop) or one of its ancestors in the tree produced by DFS. In the following graph, there are 3 back edges, marked with a cross sign. We can observe that these 3 back edges indicate 3 cycles present in the graph.
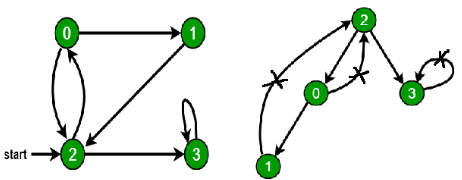
- For a disconnected graph, Get the DFS forest as output. To detect cycle, check for a cycle in individual trees by checking back edges.
To detect a back edge, keep track of vertices currently in the recursion stack of function for DFS traversal. If a vertex is reached that is already in the recursion stack, then there is a cycle in the tree. The edge that connects the current vertex to the vertex in the recursion stack is a back edge. Use recStack[] array to keep track of vertices in the recursion stack.
Dry run of the above approach: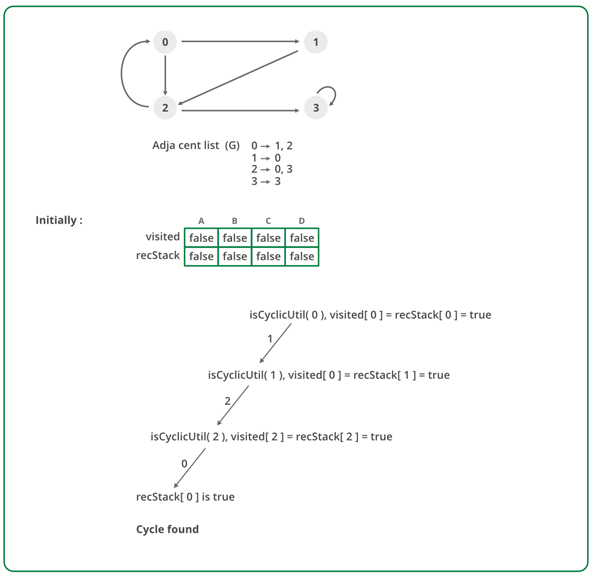
- Algorithm:
(i) Create the graph using the given number of edges and vertices.
(ii) Create a recursive function that initializes the current index or vertex, visited, and recursion stack.
(iii) Mark the current node as visited and also mark the index in recursion stack.
(iv) Find all the vertices which are not visited and are adjacent to the current node. Recursively call the function for those vertices, If the recursive function returns true, return true.
(v) If the adjacent vertices are already marked in the recursion stack then return true.
(vi) Create a wrapper class, that calls the recursive function for all the vertices and if any function returns true return true. Else if for all vertices the function returns false return false.
Implementation:
- C++


- Java


- Python


- C#


Output:
Graph contains cycle
Complexity Analysis
- Time Complexity: O(V + E).
Time Complexity of this method is same as time complexity of DFS traversal which is O(V + E). - Space Complexity: O(V).
To store the visited and recursion stack O(V) space is needed.
Longest Path in a Directed Acyclic Graph
Given a Weighted Directed Acyclic Graph (DAG) and a source vertex s in it, find the longest distances from s to all other vertices in the given graph.
The longest path problem for a general graph is not as easy as the shortest path problem because the longest path problem doesn’t have optimal substructure property. In fact, the Longest Path problem is NP-Hard for a general graph. However, the longest path problem has a linear time solution for directed acyclic graphs. The idea is similar to linear time solution for shortest path in a directed acyclic graph., we use Topological Sorting.
We initialize distances to all vertices as minus infinite and distance to source as 0, then we find a topological sorting of the graph. Topological Sorting of a graph represents a linear ordering of the graph (See below, figure (b) is a linear representation of figure (a) ). Once we have topological order (or linear representation), we one by one process all vertices in topological order. For every vertex being processed, we update distances of its adjacent using distance of current vertex.
Following figure shows step by step process of finding longest paths: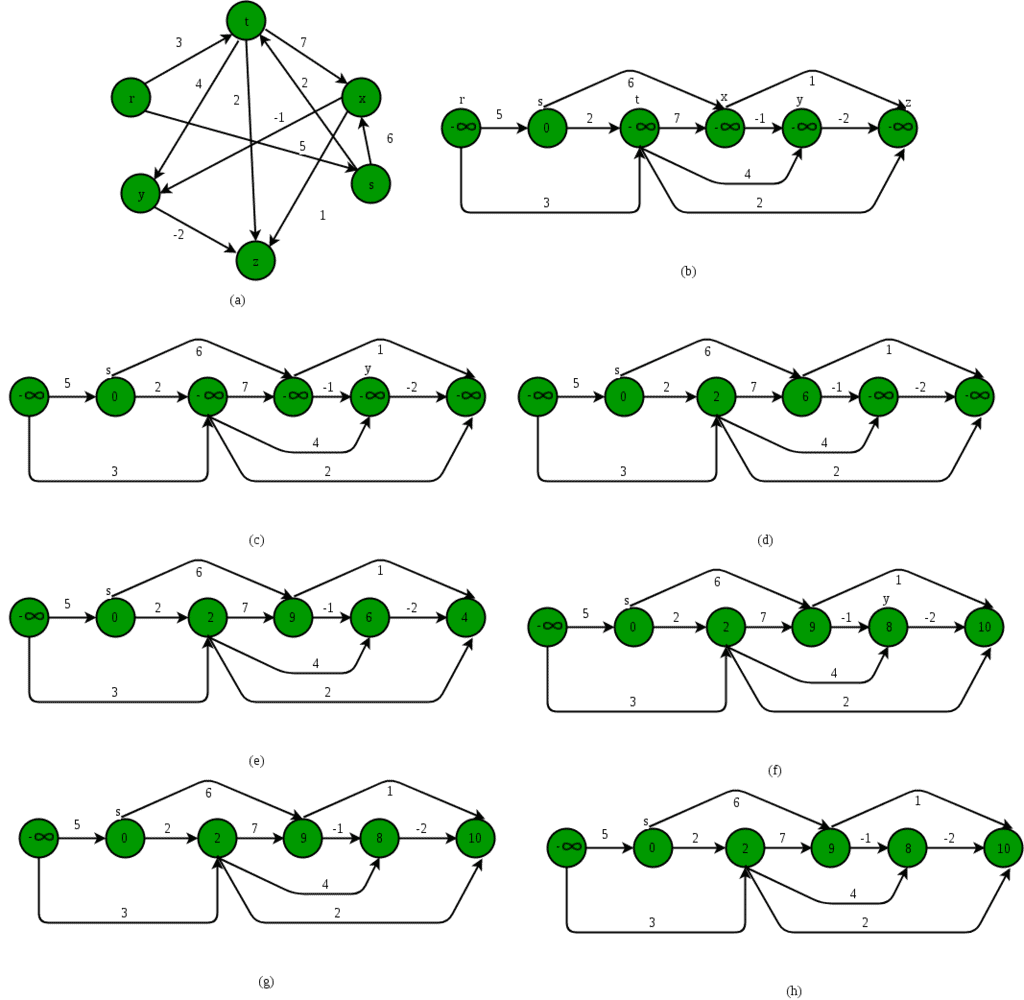
Following is complete algorithm for finding longest distances:
- Initialize dist[] = {NINF, NINF, ….} and dist[s] = 0 where s is the source vertex. Here NINF means negative infinite.
- Create a toplogical order of all vertices.
- Do following for every vertex u in topological order.
………..Do following for every adjacent vertex v of u
………………if (dist[v] < dist[u] + weight(u, v))
………………………dist[v] = dist[u] + weight(u, v)
Following is C++ implementation of the above algorithm:
- CPP




- Java



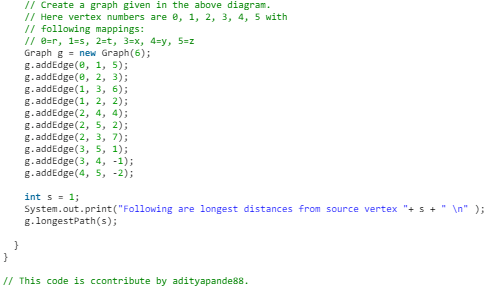
- Python3


Output:
Following are longest distances from source vertex 1
INF 0 2 9 8 10
Time Complexity: Time complexity of topological sorting is O(V + E). After finding topological order, the algorithm process all vertices and for every vertex, it runs a loop for all adjacent vertices. Total adjacent vertices in a graph is O(E). So the inner loop runs O(V + E) times. Therefore, overall time complexity of this algorithm is O(V + E).
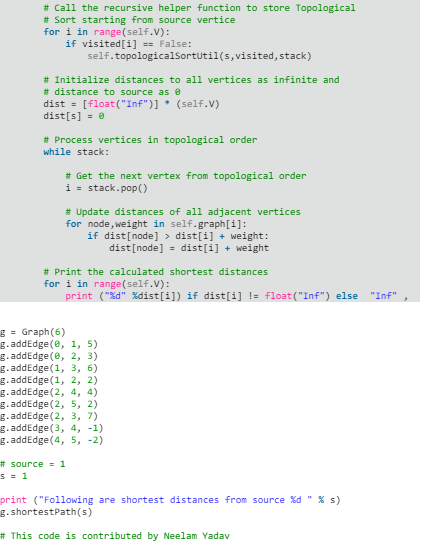
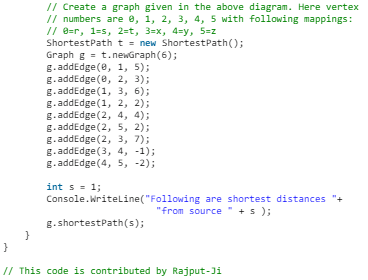
Shortest Path in Directed Acyclic Graph
Given a Weighted Directed Acyclic Graph and a source vertex in the graph, find the shortest paths from given source to all other vertices.
For a general weighted graph, we can calculate single source shortest distances in O(VE) time using Bellman–Ford Algorithm. For a graph with no negative weights, we can do better and calculate single source shortest distances in O(E + VLogV) time using Dijkstra’s algorithm. Can we do even better for Directed Acyclic Graph (DAG)? We can calculate single source shortest distances in O(V + E) time for DAGs. The idea is to use Topological Sorting.
We initialize distances to all vertices as infinite and distance to source as 0, then we find a topological sorting of the graph. Topological Sorting of a graph represents a linear ordering of the graph (See below, figure (b) is a linear representation of figure (a) ). Once we have topological order (or linear representation), we one by one process all vertices in topological order. For every vertex being processed, we update distances of its adjacent using distance of current vertex.
Following figure is taken from this source. It shows step by step process of finding shortest paths: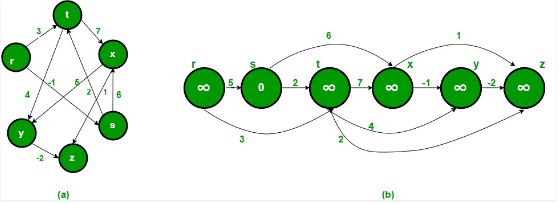
Following is complete algorithm for finding shortest distances:
- Initialize dist[] = {INF, INF, ….} and dist[s] = 0 where s is the source vertex.
- Create a toplogical order of all vertices.
- Do following for every vertex u in topological order.
………..Do following for every adjacent vertex v of u
………………if (dist[v] > dist[u] + weight(u, v))
………………………dist[v] = dist[u] + weight(u, v)
- C++




- Java




- Python

- C#



Output:
Following are shortest distances from source 1
INF 0 2 6 5 3
Time Complexity: Time complexity of topological sorting is O(V + E). After finding topological order, the algorithm process all vertices and for every vertex, it runs a loop for all adjacent vertices. Total adjacent vertices in a graph is O(E). So the inner loop runs O(V + E) times. Therefore, overall time complexity of this algorithm is O(V + E).
|
81 videos|113 docs|33 tests
|















