Bridges in a graph | Algorithms - Computer Science Engineering (CSE) PDF Download
Bridges in a graph
An edge in an undirected connected graph is a bridge iff removing it disconnects the graph. For a disconnected undirected graph, definition is similar, a bridge is an edge removing which increases number of disconnected components.
Like Articulation Points, bridges represent vulnerabilities in a connected network and are useful for designing reliable networks. For example, in a wired computer network, an articulation point indicates the critical computers and a bridge indicates the critical wires or connections.
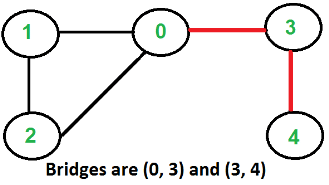
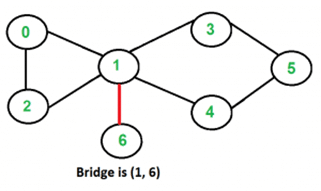
Following are some example graphs with bridges highlighted with red color:
How to find all bridges in a given graph?
A simple approach is to one by one remove all edges and see if removal of an edge causes disconnected graph. Following are steps of simple approach for connected graph.
- For every edge (u, v), do following
…..a) Remove (u, v) from graph
..…b) See if the graph remains connected (We can either use BFS or DFS)
…..c) Add (u, v) back to the graph.
Time complexity of above method is O(E * (V + E)) for a graph represented using adjacency list. Can we do better?
A O(V + E) algorithm to find all Bridges
The idea is similar to O(V + E) algorithm for Articulation Points. We do DFS traversal of the given graph. In DFS tree an edge (u, v) (u is parent of v in DFS tree) is bridge if there does not exist any other alternative to reach u or an ancestor of u from subtree rooted with v. As discussed in the previous post, the value low[v] indicates earliest visited vertex reachable from subtree rooted with v. The condition for an edge (u, v) to be a bridge is, “low[v] > disc[u]”.
Following are C++ and Java implementations of above approach:- C++



- Java




- Python

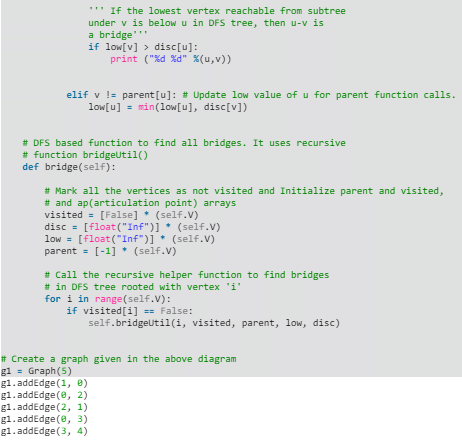

- C#




Output:
- Bridges in first graph
3 4
0 3 - Bridges in second graph
2 3
1 2
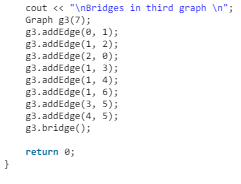
0 1 - Bridges in third graph
1 6
Time Complexity: The above function is simple DFS with additional arrays. So time complexity is same as DFS which is O(V + E) for adjacency list representation of graph.
|
81 videos|113 docs|33 tests
|
FAQs on Bridges in a graph - Algorithms - Computer Science Engineering (CSE)
| 1. What is a bridge in a graph? |  |
| 2. How can we identify bridges in a graph? |  |
| 3. Why are bridges important in graph theory? |  |
| 4. Can a graph have multiple bridges? |  |
| 5. How can the knowledge of bridges in a graph be applied practically? |  |
















