Activity Selection Problem | Algorithms - Computer Science Engineering (CSE) PDF Download
Greedy Algo-1
Greedy is an algorithmic paradigm that builds up a solution piece by piece, always choosing the next piece that offers the most obvious and immediate benefit. Greedy algorithms are used for optimization problems. An optimization problem can be solved using Greedy if the problem has the following property: At every step, we can make a choice that looks best at the moment, and we get the optimal solution of the complete problem.
If a Greedy Algorithm can solve a problem, then it generally becomes the best method to solve that problem as the Greedy algorithms are in general more efficient than other techniques like Dynamic Programming. But Greedy algorithms cannot always be applied. For example, the Fractional Knapsack problem (See this) can be solved using Greedy, but 0-1 Knapsack cannot be solved using Greedy.
Following are some standard algorithms that are Greedy algorithms:
- Kruskal’s Minimum Spanning Tree (MST): In Kruskal’s algorithm, we create a MST by picking edges one by one. The Greedy Choice is to pick the smallest weight edge that doesn’t cause a cycle in the MST constructed so far.
- Prim’s Minimum Spanning Tree: In Prim’s algorithm also, we create a MST by picking edges one by one. We maintain two sets: a set of the vertices already included in MST and the set of the vertices not yet included. The Greedy Choice is to pick the smallest weight edge that connects the two sets.
- Dijkstra’s Shortest Path: Dijkstra’s algorithm is very similar to Prim’s algorithm. The shortest-path tree is built up, edge by edge. We maintain two sets: a set of the vertices already included in the tree and the set of the vertices not yet included. The Greedy Choice is to pick the edge that connects the two sets and is on the smallest weight path from source to the set that contains not yet included vertices.
- Huffman Coding: Huffman Coding is a loss-less compression technique. It assigns variable-length bit codes to different characters. The Greedy Choice is to assign the least bit length code to the most frequent character.
The greedy algorithms are sometimes also used to get an approximation for Hard optimization problems. For example, Traveling Salesman Problem is an NP-Hard problem. A Greedy choice for this problem is to pick the nearest unvisited city from the current city at every step. These solutions don’t always produce the best optimal solution but can be used to get an approximately optimal solution.
Let us consider the Activity Selection problem as our first example of Greedy algorithms. Following is the problem statement.
You are given n activities with their start and finish times. Select the maximum number of activities that can be performed by a single person, assuming that a person can only work on a single activity at a time.
Example
Example 1: Consider the following 3 activities sorted by by finish time.
start[] = {10, 12, 20};
finish[] = {20, 25, 30};
A person can perform at most two activities. The maximum set of activities that can be executed is {0, 2} [ These are indexes in start[] and finish[] ]
Example 2: Consider the following 6 activities sorted by by finish time.
start[] = {1, 3, 0, 5, 8, 5};
finish[] = {2, 4, 6, 7, 9, 9};
A person can perform at most four activities. The maximum set of activities that can be executed is {0, 1, 3, 4} [ These are indexes in start[] and finish[] ]
The greedy choice is to always pick the next activity whose finish time is least among the remaining activities and the start time is more than or equal to the finish time of the previously selected activity. We can sort the activities according to their finishing time so that we always consider the next activity as minimum finishing time activity.
- Sort the activities according to their finishing time
- Select the first activity from the sorted array and print it.
- Do the following for the remaining activities in the sorted array.
…….a) If the start time of this activity is greater than or equal to the finish time of the previously selected activity then select this activity and print it.
In the following C implementation, it is assumed that the activities are already sorted according to their finish time.
- C++

- C

- Java

- C#


- Python

- PHP

- Javascript

Output: Following activities are selected n0 1 3 4
How does Greedy Choice work for Activities sorted according to finish time?
Let the given set of activities be S = {1, 2, 3, …n} and activities are sorted by finish time. The greedy choice is to always pick activity 1. How come activity 1 always provides one of the optimal solutions. We can prove it by showing that if there is another solution B with the first activity other than 1, then there is also a solution A of the same size with activity 1 as the first activity. Let the first activity selected by B be k, then there always exist A = {B – {k}} U {1}.
Note that the activities in B are independent and k has the smallest finishing time among all. Since k is not 1, finish(k) >= finish(1).
How to implement when given activities are not sorted?
We create a structure/class for activities. We sort all activities by finish time (Refer sort in C++ STL). Once we have activities sorted, we apply the same algorithm.
Below image is an illustration of the above approach: 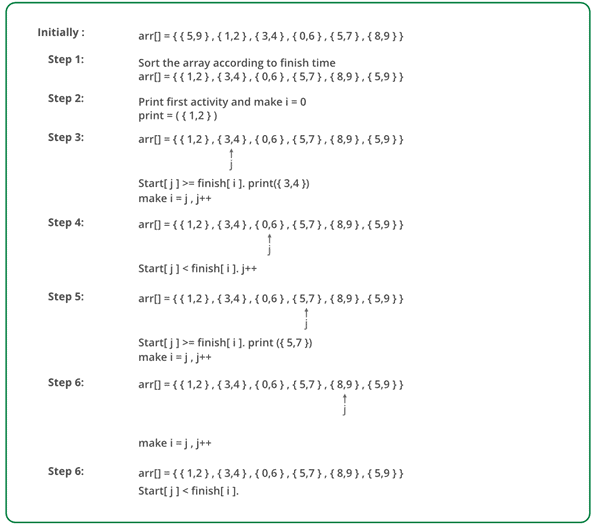
Below is the implementation of the above approach:
- C++


- Java


- Python3

- Javascript

Output: Following activities are selected
(1, 2), (3, 4), (5, 7), (8, 9),
Time Complexity: It takes O(n log n) time if input activities may not be sorted. It takes O(n) time when it is given that input activities are always sorted.
Using STL we can solve it as follows:
- CPP

- Java


Output
Following Activities should be selected:
- Activity started at: 1 and ends at 2
- Activity started at: 3 and ends at 4
- Activity started at: 5 and ends at 7
- Activity started at: 8 and ends at 9
|
81 videos|107 docs|33 tests
|
FAQs on Activity Selection Problem - Algorithms - Computer Science Engineering (CSE)
| 1. What is the Activity Selection Problem in Computer Science Engineering (CSE)? |  |
| 2. How does the Greedy Algorithm solve the Activity Selection Problem? |  |
| 3. What is the time complexity of the Greedy Algorithm for the Activity Selection Problem? |  |
| 4. Can the Greedy Algorithm be used for all scheduling problems in Computer Science Engineering (CSE)? |  |
| 5. What are the advantages of using the Greedy Algorithm for the Activity Selection Problem? |  |
















