Closest Pair of Points | Algorithms - Computer Science Engineering (CSE) PDF Download
Closest Pair of Points using Divide and Conquer algorithm
We are given an array of n points in the plane, and the problem is to find out the closest pair of points in the array. This problem arises in a number of applications. For example, in air-traffic control, you may want to monitor planes that come too close together, since this may indicate a possible collision. Recall the following formula for distance between two points p and q.
The Brute force solution is O(n^2), compute the distance between each pair and return the smallest. We can calculate the smallest distance in O(nLogn) time using Divide and Conquer strategy. In this post, a O(n x (Logn)^2) approach is discussed. We will be discussing a O(nLogn) approach in a separate post.
Algorithm
Following are the detailed steps of a O(n (Logn)^2) algortihm.
Input: An array of n points P[]
Output: The smallest distance between two points in the given array.
As a pre-processing step, the input array is sorted according to x coordinates.
- Find the middle point in the sorted array, we can take P[n/2] as middle point.
- Divide the given array in two halves. The first subarray contains points from P[0] to P[n/2]. The second subarray contains points from P[n/2+1] to P[n-1].
- Recursively find the smallest distances in both subarrays. Let the distances be dl and dr. Find the minimum of dl and dr. Let the minimum be d.
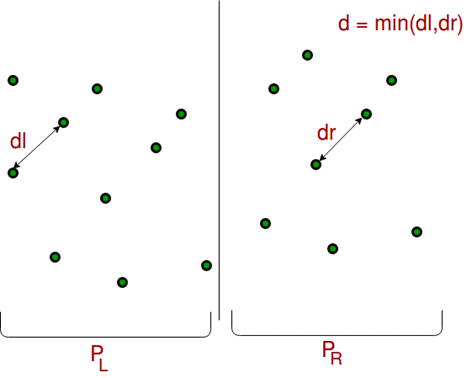
- From the above 3 steps, we have an upper bound d of minimum distance. Now we need to consider the pairs such that one point in pair is from the left half and the other is from the right half. Consider the vertical line passing through P[n/2] and find all points whose x coordinate is closer than d to the middle vertical line. Build an array strip[] of all such points.
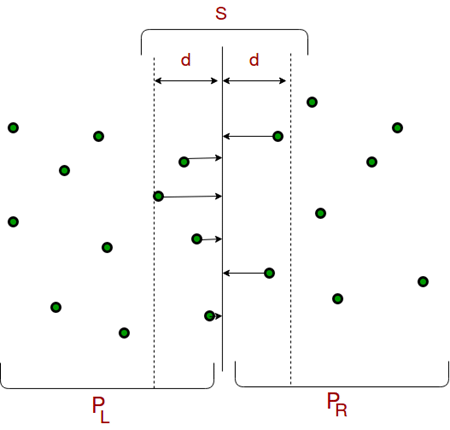
- Sort the array strip[] according to y coordinates. This step is O(nLogn). It can be optimized to O(n) by recursively sorting and merging.
- Find the smallest distance in strip[]. This is tricky. From the first look, it seems to be a O(n^2) step, but it is actually O(n). It can be proved geometrically that for every point in the strip, we only need to check at most 7 points after it (note that strip is sorted according to Y coordinate). See this for more analysis.
- Finally return the minimum of d and distance calculated in the above step (step 6)
Implementation
Following is the implementation of the above algorithm.
C++





C





Python3




Output:
The smallest distance is 1.414214
Time Complexity: Let Time complexity of above algorithm be T(n). Let us assume that we use a O(nLogn) sorting algorithm. The above algorithm divides all points in two sets and recursively calls for two sets. After dividing, it finds the strip in O(n) time, sorts the strip in O(nLogn) time and finally finds the closest points in strip in O(n) time. So T(n) can expressed as follows
T(n) = 2T(n / 2) + O(n) + O(nLogn) + O(n)
T(n) = 2T(n / 2) + O(nLogn)
T(n) = T(n x Logn x Logn)
Notes
- Time complexity can be improved to O(nLogn) by optimizing step 5 of the above algorithm. We will soon be discussing the optimized solution in a separate post.
- The code finds smallest distance. It can be easily modified to find the points with the smallest distance.
- The code uses quick sort which can be O(n^2) in the worst case. To have the upper bound as O(n (Logn)^2), a O(nLogn) sorting algorithm like merge sort or heap sort can be used
|
81 videos|113 docs|33 tests
|
















