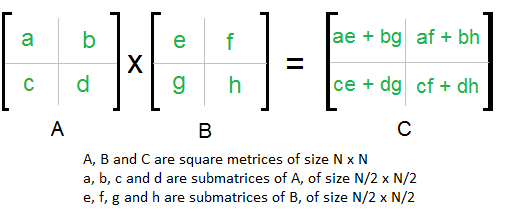Computer Science Engineering (CSE) Exam > Computer Science Engineering (CSE) Notes > Algorithms > Strassen’s Matrix Multiplication
Strassen’s Matrix Multiplication | Algorithms - Computer Science Engineering (CSE) PDF Download
Given two square matrices A and B of size n x n each, find their multiplication matrix.
Methods
- Naive Method
Following is a simple way to multiply two matrices:
(i) C
(ii) Javascript
Time Complexity of above method is O(N3). - Divide and Conquer
Following is simple Divide and Conquer method to multiply two square matrices:
(i) Divide matrices A and B in 4 sub-matrices of size N/2 x N/2 as shown in the below diagram.
(ii) Calculate following values recursively. ae + bg, af + bh, ce + dg and cf + dh.
In the above method, we do 8 multiplications for matrices of size N/2 x N/2 and 4 additions. Addition of two matrices takes O(N2) time. So the time complexity can be written as
T(N) = 8T(N / 2) + O(N2)
From Master's Theorem, time complexity of above method is O(N3)
which is unfortunately same as the above naive method.
Simple Divide and Conquer also leads to O(N3), can there be a better way?
In the above divide and conquer method, the main component for high time complexity is 8 recursive calls. The idea of Strassen’s method is to reduce the number of recursive calls to 7. Strassen’s method is similar to above simple divide and conquer method in the sense that this method also divide matrices to sub-matrices of size N/2 x N/2 as shown in the above diagram, but in Strassen’s method, the four sub-matrices of result are calculated using following formulae.
- Time Complexity of Strassen’s Method
Addition and Subtraction of two matrices takes O(N2) time. So time complexity can be written as
T(N) = 7T(N/2) + O(N2)
From Master's Theorem, time complexity of above method is
O(NLog7) which is approximately O(N2.8074)
Generally, Strassen’s Method is not preferred for practical applications for following reasons.
(i) The constants used in Strassen’s method are high and for a typical application Naive method works better.
(ii) For Sparse matrices, there are better methods especially designed for them.
(iii) The submatrices in recursion take extra space.
(iv) Because of the limited precision of computer arithmetic on noninteger values, larger errors accumulate in Strassen’s algorithm than in Naive Method
Python

The document Strassen’s Matrix Multiplication | Algorithms - Computer Science Engineering (CSE) is a part of the Computer Science Engineering (CSE) Course Algorithms.
All you need of Computer Science Engineering (CSE) at this link: Computer Science Engineering (CSE)
|
81 videos|80 docs|33 tests
|
FAQs on Strassen’s Matrix Multiplication - Algorithms - Computer Science Engineering (CSE)
| 1. What is Strassen's matrix multiplication algorithm? |  |
Ans. Strassen's matrix multiplication algorithm is an efficient algorithm used to multiply two matrices. It reduces the number of basic multiplications required by recursively breaking down the matrices into smaller submatrices and performing mathematical operations on them.
| 2. How does Strassen's matrix multiplication algorithm work? |  |
Ans. Strassen's algorithm works by dividing each input matrix into four equally-sized submatrices. It then recursively computes the products of these submatrices using a set of mathematical formulas that involve addition and subtraction operations. Finally, it combines these intermediate results to obtain the final matrix product.
| 3. What is the advantage of using Strassen's algorithm over traditional matrix multiplication? |  |
Ans. The advantage of using Strassen's algorithm is that it reduces the number of basic multiplications required to compute the matrix product. This results in a faster algorithm for large matrices, as the time complexity of Strassen's algorithm is O(n^(log2(7))) compared to the traditional O(n^3) time complexity.
| 4. Are there any limitations or drawbacks of Strassen's matrix multiplication algorithm? |  |
Ans. Yes, there are limitations to Strassen's algorithm. It requires the input matrices to have dimensions that are powers of 2, and the dimensions must be equal. Additionally, the algorithm involves more complex mathematical operations, such as matrix additions and subtractions, which can add overhead compared to traditional matrix multiplication for small matrices.
| 5. Can Strassen's algorithm be extended to multiply matrices of different dimensions? |  |
Ans. No, Strassen's algorithm cannot be directly extended to multiply matrices of different dimensions. It relies on dividing the matrices into equally-sized submatrices, which is not possible when the dimensions are different. However, there are techniques such as padding or zero-padding that can be used to make the dimensions equal before applying Strassen's algorithm.

|
Explore Courses for Computer Science Engineering (CSE) exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
Related Searches